Chirp (FPScript)
Calculates a swept-frequency cosine, i.e. a cosine signal with a variable frequency.
Syntax
Chirp(Time, Frequency1, Frequency2, Time2 [ , Operation = CHIRP_LINEAR ])
The syntax of the Chirp function consists of the following parts:
Part |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Time |
A data set with the time for which the swept-frequency cosine is to be calculated. All data structures are allowed. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||||||
Frequency1 |
The frequency that the swept-frequency cosine is to have for Time = 0. Permitted data structures are scalar value. All real data types are permitted. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
Frequency2 |
The frequency that the swept-frequency cosine is to have for the Time2 point in time. Permitted data structures are scalar value. All real data types are permitted. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
Time2 |
The time for which the swept-frequency cosine is to have the Frequency2 frequency. Permitted data structures are scalar value. All real data types are permitted. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
Operation |
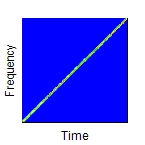
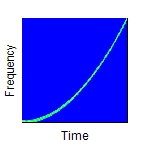
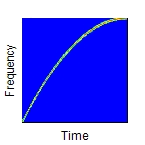
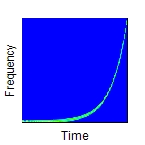
Determines the type of frequency variation. The argument Operation can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value CHIRP_LINEAR. |
Remarks
The data type of the result is always 64-bit floating point.
The structure of the result corresponds to that of the argument Time. The calculation is done element-by-element where appropriate.
The result has the unit 1, if Time has a unit. Otherwise, it has no unit.
For aggregate data structures, only the Y component is considered and the X or, if applicable, Z component is copied into the result without modification.
Available in
FlexPro Basic, Professional, Developer Suite
Examples
Dim x = Series(0 s, 10 s, 0.001 s) |
Generates a swept-frequency cosine signal with a sampling rate of 1 kHz in the time range from 0 s to 10 s with a linear frequency course from 10 Hz to 100 Hz. |