Analyseobjekt Spline-Interpolation *
Mit diesem Analyseobjekt können Sie eine Spline-Interpolation für Ihre Daten durchführen, d. h. eine möglichst glatte Kurve berechnen, die die Punkte Ihres Datensatzes verbindet. Die Spline-Interpolation ist in die Liniengrafik von FlexPro direkt integriert, so dass Sie dieses Analyseobjekt nur dann benötigen, wenn Sie die geglätteten Daten mathematisch weiterverarbeiten möchten.
Die Spline-Interpolation verbindet alle benachbarten Punkte des Kurvenzuges durch Polynome dritten Grades, also Funktionen von der Form:
![]()
Jeweils zwei Polynome stoßen an einem Punkt des Kurvenzuges zusammen. Eine Ausnahme bilden der erste und letzte Punkt des Kurvenzuges. Die Koeffizienten ai, bi, ci und di der Polynome werden so gewählt, dass die benachbarten Polynome an den Stellen, an denen Sie zusammenstoßen in Ort, Steigung und Krümmung übereinstimmen. Für den ersten und letzten Punkt, an dem ja keine Polynome aneinander stoßen, können Sie das Aussehen der Spline-Kurve durch so genannte Randbedingungen beeinflussen, d. h. Sie geben entweder Steigung oder Krümmung der Spline-Kurve am linken und rechten Rand vor. Je nach Art der Randbedingungen erhalten Sie ein unterschiedliches Aussehen der Spline-Kurve, wie in der folgenden Abbildung gezeigt:
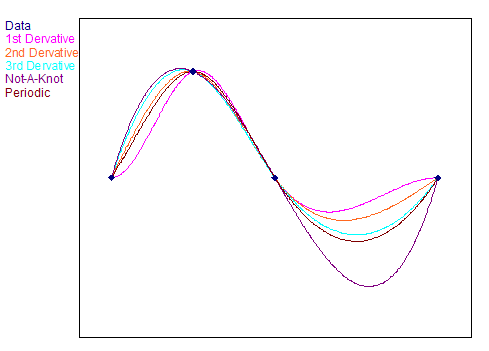
Hervorzuheben sind hier:
•Natürliche Splines. Diese erhalten Sie, wenn Sie als Randbedingung Krümmungen wie angegeben wählen und als Werte für die Krümmungen an beiden Rändern den Wert Null eintragen. Das Aussehen entspricht der Kurve, die Sie erhalten würden, wenn Sie die Punkte des Kurvenzuges mit einem Gummilineal verbinden würden.
•Ausgleichende Splines. Hier geht die berechnete Kurve nicht zwingend durch die vorgegebenen Stützpunkte. Die Kurve kann über einen Gewichtsfaktor in ihrer Welligkeit gesteuert werden. Wenn der Gewichtsfaktor nahe bei Null liegt, ergibt sich die Bestgerade bzgl. des quadratischen Fehlers als Spline-Kurve. Für einen sehr großen Gewichtsfaktor erhalten Sie eine natürliche Spline-Kurve, was den oben angegebenen Randbedingungen entspricht. In diesem Fall folgt die Spline-Kurve in ihrem Verlauf den Punkten des Kurvenzuges.
•Periodische Splines entstehen durch die Forderung, dass die Spline-Kurve in Steigung und Krümmung am linken und rechten Rand übereinstimmen soll. Die entstehende Spline-Kurve könnten Sie dann mehrfach hintereinander hängen, ohne dass an den Nahtstellen ein Knick entsteht. Zur Berechnung einer periodischen Spline-Interpolation müssen der Y-Wert von erstem und letztem Punkt übereinstimmen. Ist dies nicht der Fall, dann verwendet FlexPro eines von zwei Verfahren, um die Periodizität zu erzwingen. Wenn Sie Periodisch, Periodizität durch Ersetzen wählen, dann wird der letzte Y-Wert im Datensatz ignoriert und stattdessen eine Kopie des ersten Y-Wertes verwendet. Bei Auswahl von Periodisch, Periodizität durch Anhängen wird dagegen, falls der letzte Y-Wert im Datensatz nicht identisch mit dem ersten ist, eine Kopie des ersten Y-Wertes an den Datensatz angehängt. Als X-Wert für diesen zusätzlichen Punkt wird der X-Wert des ursprünglich letzten Punktes plus der Differenz zwischen letztem und vorletztem X-Wert verwendet.
•Splines mit "Not-A-Knot" Randbedingung. Diese verwenden je zwei identische Polynome am linken und rechten Rand, was der Bedingung entspricht, dass die dritte Ableitung der Spline-Funktionen im zweiten und vorletzten Datenpunkt stetig sind. Dadurch sind diese Punkte keine echten Knoten der Spline-Kurve.
Voraussetzung für die Spline-Interpolation ist, dass die X-Werte der Punkte streng monoton wachsend sind. Ist dies nicht der Fall (z. B. bei einer Ortskurve), so sollten Sie die parametrische Spline-Interpolation verwenden. Die X-Werte müssen jedoch nicht äquidistant sein. Nachdem die Koeffizienten der Spline-Kurve berechnet sind, kann FlexPro die berechnete Spline-Funktion an beliebigen Stellen auswerten, um neue Stützstellen zu erhalten.
Die folgende Abbildung zeigt ausgleichende Splines mit verschiedenen Gewichtsfaktoren:
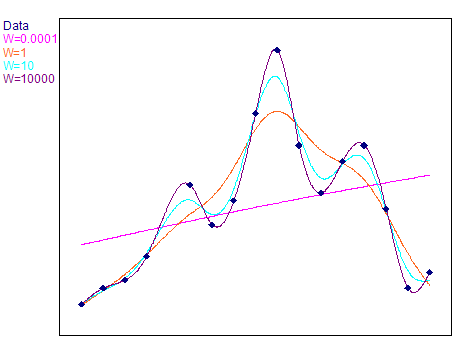
Das Ergebnis der Spline-Interpolation ist zunächst ein mathematisches Modell des zu interpolierenden Datensatzes. Der Auswertungsmodus gibt an, an welchen Punkten die berechnete Spline-Kurve ausgewertet werden soll, um den Ergebnisdatensatz zu erhalten. Folgende Auswertemodi sind möglich:
•N-Werte äquidistant: Die Spline-Kurve wird in diesem Fall an N äquidistanten Stützstellen ausgewertet, unabhängig davon, wie die X-Werte vorher verteilt waren.
•N-Werte pro X-Intervall: In diesem Fall wird jedes vorherige X-Intervall in N gleich große Intervalle unterteilt, an deren Grenzen die Spline-Funktion ausgewertet wird.
Die folgende Abbildung zeigt die Arbeitsweise der beiden Auswertemodi:
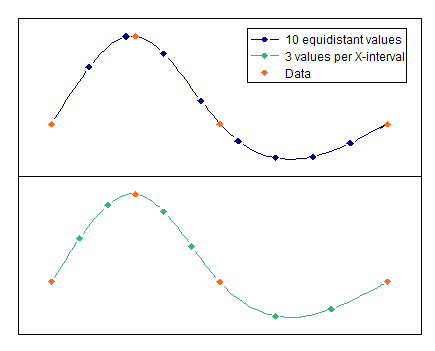
Verwendete FPScript-Funktionen
Siehe auch
Analyseobjekt Parametrische Spline-Interpolation
Analyseobjekt Lineare Interpolation
* Dieses Analyseobjekt ist in FlexPro View nicht verfügbar.
