MatrixMultiplication (FPScript)
Multipliziert Matrizen mit Vektoren und Matrizen in allen Kombinationen.
Syntax
MatrixMultiplication(A, B)
Die Syntax der MatrixMultiplication-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
A |
Ist die linke Datenreihe bzw. die linke Datenmatrix. Erlaubte Datenstrukturen sind Datenreihe und Datenmatrix. Es sind alle numerischen Datentypen erlaubt. |
B |
Ist die rechte Datenreihe bzw. die rechte Datenmatrix. Erlaubte Datenstrukturen sind Datenreihe und Datenmatrix. Es sind alle numerischen Datentypen erlaubt. |
Anmerkungen
Die Einheit des Ergebnisses ist gleich dem Produkt der Einheiten von A und B. Die Argumente A und B liefern die zu multiplizierenden Matrizen bzw. Vektoren. Matrizen werden hierbei als Datenmatrizen, bei denen die Datenreihen darin den Zeilen entsprechen, und Vektoren als Datenreihen übergeben.
Bei komplexen Argumenten erfolgt eine komplexe Multiplikation und das Ergebnis ist ebenfalls komplex. Das Ergebnis ist immer vom gleichen Datentyp wie die Argumente. Wenn die Argumente verschiedene Datentypen haben, werden diese so angepasst, dass kein Auflösungsverlust beim Ergebnis erfolgt, d. h. niedrigere Auflösungen werden zu höheren gewandelt, Ganzzahlen zu Fließkommazahlen und reelle Zahlen zu komplexen Zahlen.
Die komplexe Multiplikation ist definiert als (a, b) * (c, d) = (a * c - b * d, a * d + b * c).
Das Ergebnis hat den gleichen Datentyp wie das ggf. gewandelte Argument. Folgende Operationen werden durchgeführt:
Vektor mit Vektor: Es wird das Skalarprodukt der beiden Vektoren A und B gebildet.
Beispiel für Vektoren mit drei Elementen:
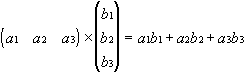
Matrix mit Vektor: Jede Zeile der Matrix A wird vektoriell mit dem Vektor B multipliziert. Die Zeilenzahl der Matrix A muss mit der Anzahl der Elemente von Vektor B übereinstimmen.
Beispiel für eine 3x3-Matrix A und Vektor B mit drei Elementen:
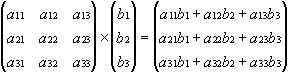
Vektor mit Matrix: Jede Spalte der Matrix B wird vektoriell mit dem Vektor A multipliziert wobei die Anzahl der Spalten der Matrix mit der Anzahl der Elemente des Vektors übereinstimmen muss.
Beispiel für eine 3x3-Matrix und einen Vektor mit drei Elementen:
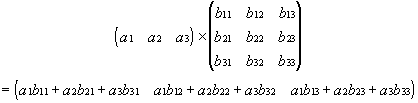
Matrix mit Matrix: Jede Zeile der Matrix A wird mit jeder Spalte der Matrix B vektoriell multipliziert. Die Anzahl der Zeilen der Matrix A muss mit der Anzahl der Spalten der Matrix B übereinstimmen.
Beispiel für zwei 3x3-Matrizen:

Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste.
Hinweis Bitte beachten Sie, dass die Datenreihen in der Datenmatrix als die Zeilen der Matrix interpretiert werden, obwohl diese im Datensatzfenster als Spalten angezeigt werden. Diese Zuordnung ist nötig, damit der Indexoperator für Matrizen mit der durch die Matrizenrechnung vorgegebenen Reihenfolge "Zeilen zuerst, Spalten später" angewendet werden kann.
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
MatrixMultiplication({2, 4, 6}, {2, 3, 4}) |
Ergibt 40. (das Skalarprodukt der beiden Vektoren) |
