Analyseobjekt und -vorlage FIR-Filter (Equiripple-Methode) (Option Digitale Filter)
Mit diesem Analyseobjekt können Sie Signale filtern. Es werden Tiefpass, Hochpass, Bandpass, Bandsperre und Multibandfilter mit verschiedenen Charakteristika angeboten.
Das Objekt arbeitet mit Finite-Impulse-Response (FIR) Filtern, die mithilfe der FIR-Equiripple-Methode berechnet werden.
Ergebnis
Als Ergebnis können die berechneten Filterkoeffizienten ausgegeben werden. Das Ergebnis entspricht der Impulsantwort des Filters. In diesem Fall muss kein Eingangsdatensatz angegeben werden. Alternativ kann das Ergebnis ein Signal sein, das mit dem zuvor berechneten FIR-Filter gefiltert wird. Hierzu muss in der Registerkarte Daten ein zu filternder Datensatz ausgewählt werden. Im Gegensatz zum Ergebnis Gefiltertes Signal findet beim Ergebnis Gefiltertes Signal mit Phasenkorrektur eine Phasenkorrektur statt (τ = T/2 (L - 1), falls Filter ungerade; τ = LT/2, falls Filter gerade (L = Filterlänge)).
Filtervorlage
Es existieren die vordefinierten Vorlagen Tiefpass, Hochpass, Bandpass, Bandsperre und Multiband. Mit Ausnahme des Multiband-Filters können in der Liste Bänder keine weiteren Bänder hinzugefügt und keine Bänder gelöscht werden. Außerdem sind die Verstärkungsfaktoren vordefiniert. Allerdings lassen sich die Eckfrequenzen des Übergangbereichs und die Fehler/Gewichtungen ändern. Es besteht auch die Möglichkeit, eigene Filtervorlagen zu erstellen. Dazu editieren Sie die Bänder, geben einen Filternamen unter Filtervorlage ein und drücken die Speichern-Schaltfläche. Eigene Vorlagen lassen sich natürlich auch wieder löschen. Die Vorlagen speichert FlexPro in Ihrem Benutzerprofil.
Filterlänge
Die Filterlänge bestimmt die Steilheit des Filters. Je länger das Filter, desto höher ist auch die Steilheit des Filters. Es ist möglich, eine feste Länge anzugeben oder die Länge des Filters zu schätzen. In diesem Fall wird der optimale Filter gemäß der vorhandenen Spezifikation berechnet. Wird eine feste Filterlänge angegeben, so lässt sich nur eine Gewichtung für die einzelnen Bänder angeben, da nicht sichergestellt ist, dass eine gewünschte Fehlertoleranz erreicht werden kann. Lässt man die Filterlänge berechnen, so werden die absoluten Fehler für die Bänder angegeben.
Verstärkungsfaktor
Für jedes Band können jeweils zwei Verstärkungsfaktoren definiert werden. Der erste Wert ist der Verstärkungsfaktor bei der unteren Bandgrenze und der zweite Wert ist der Verstärkungsfaktor bei der oberen Bandgrenze. 0 definiert einen Sperrbereich und 1 definiert einen Durchlassbereich. Alternativ ist es möglich, die Verstärkungsfaktoren als Datensatz zu anzugeben. Der Datensatz kann entweder als Datenmatrix oder als Signal angegeben werden. Die Datenmatrix muss für jedes Band eine Spalte mit zwei Werten enthalten, die die Verstärkungsfaktoren den Bandgrenzen zuordnen. Das Signal ordnet den normierten Frequenzen von 0 bis 0,5 Verstärkungsfaktoren zu. Hiermit können Sie einen kontinuierlichen Betragsverlauf definieren. Dabei werden allerdings nur die Frequenzbereiche verwendet, die in der Liste mit den Frequenzbändern definiert sind. Jedoch ist es möglich, ein einziges Band über den gesamten Frequenzbereich von 0 bis 0,5 zu definieren.
Gewichtung / Approximationsfehler
Für jedes Band wird entweder ein Approximationsfehler (Filterlänge wird berechnet) oder eine Gewichtung (feste Filterlänge) angegeben. Für die Gewichtungen sind nur die Größenverhältnisse und nicht die absoluten Werte relevant. Der sich durch die in diesem Fall feste Filterlänge ergebende Fehler wird nämlich nur auf die Bänder verteilt. Bei einem Multibandfilter mit drei Bändern besagt zum Beispiel die Gewichtungsangabe {1, 10, 1}, dass das zweite Band eine 10mal niedrigere Welligkeit als die anderen beiden Bänder hat. Dieser Bereich ist somit glatter. Die Gewichtungen können Sie auch als Datensatz angeben. Der Datensatz kann entweder als Datenreihe oder als Signal angegeben werden. Die Datenreihe muss für jedes Band genau einen Wert enthalten. Das Signal ordnet den normierten Frequenzen von 0 bis 0,5 Gewichtungen als kontinuierlichen Verlauf zu.
Bänder
Geben Sie hier die Bänder an, die das Filter spezifizieren. Um für einen Multiband-Filter ein Band vor einem bestehenden einzufügen, markieren Sie das bestehende Band und klicken Sie dann auf die Schaltfläche Band hinzufügen. Um ein Band ans Ende der Liste anzuhängen, heben Sie die Markierung auf, indem Sie den Bereich unter der Liste anklicken bevor Sie die Schaltfläche Band hinzufügen anklicken. Zum Bearbeiten eines Listenelementes müssen Sie auf dieses doppelklicken. Es gibt auch die Möglichkeit, ein Band wieder zu löschen. Es muss mindestens ein Band definiert werden.
Wenn Sie die Option Normierte Frequenzen verwenden anklicken, werden alle Frequenzangaben auf die Abtastfrequenz normiert. Ansonsten geben Sie die Frequenzen in der Einheit an, die dem Kehrwert der Zeiteinheit des zu filternden Signals entspricht. Wegen der Nyquist-Grenze sind nur Werte bis maximal 0,5 bzw. bis zur halben Abtastfrequenz zulässig.
Beispiel
Die Angaben:
Band |
Fg1 |
Fg2 |
Fg1 Verstärkung |
Fg2 Verstärkung |
Fehler |
|---|---|---|---|---|---|
1 |
0 |
0,1 |
1 |
1 |
0,01 |
2 |
0,12 |
0,3 |
0,5 |
0,5 |
0,1 |
3 |
0,32 |
0,4 |
1 |
0,5 |
0,01 |
4 |
0,42 |
0,5 |
0 |
0 |
0,1 |
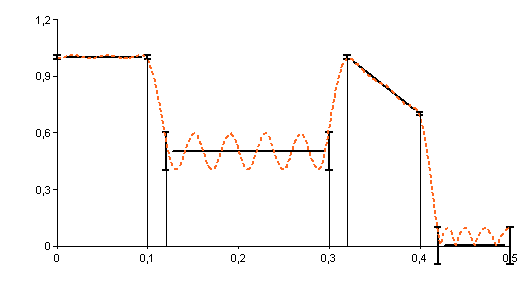
führen zu folgender Spezifikation:
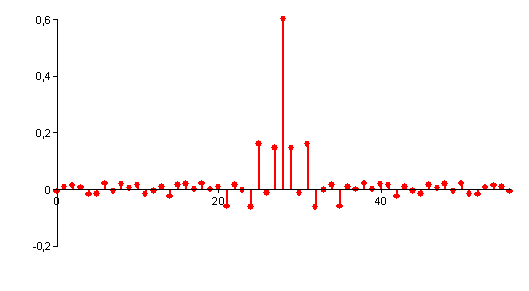
Wird die Filterlänge berechnet, so ergibt sich daraus die Impulsantwort: