Convolution (FPScript)
Berechnet das Faltungsprodukt zweier Signale.
Syntax
Convolution(Signal1, Signal2 [ , Mode = CONVOLUTION_NONCIRCULAR ])
Die Syntax der Convolution-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||
|---|---|---|---|---|---|---|---|
Signal1 |
Das Signal, das mit dem zweiten Signal gefaltet wird. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle numerischen Datentypen erlaubt. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen einen konstanten positiven Abstand haben. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
Signal2 |
Das Signal, das mit dem ersten Signal gefaltet wird. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle numerischen Datentypen erlaubt. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Die Werte müssen einen konstanten positiven Abstand haben. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
Mode |
Gibt den Berechnungsmodus an. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert CONVOLUTION_NONCIRCULAR gesetzt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die Einheit des Ergebnisses ist gleich dem Produkt der Einheiten von Signal1 und Signal2. Das Faltungsprodukt für zwei Datenreihen s und g ist definiert als:
![]()
und N, der Anzahl der Werte in s und g.
Die Berechnung erfolgt in allen Fällen im Frequenzbereich nach folgender Formel:
IRFFTn(*FFTn(Signal1) * FFTn(Signal2 ))
Bei zweidimensionalen Argumenten erfolgt die Berechnung spaltenweise und das Ergebnis ist ebenfalls zweidimensional. Hat eines der Argumente eine X-Komponente, so gilt dies auch für das Ergebnis. Das Ergebnis enthält dann den Zeitversatz τ des Faltungsproduktes. Bemerkung: Falls das andere Argument keine X-Komponente besitzt, so wird für dieses die gleiche Abtastung wie für das Argument mit X-Komponente angenommen.
Bei der zirkulären Faltung erfolgt die Berechnung unter der Annahme, dass in Signal1 und Signal2 eine oder mehrere vollständige Perioden der zu analysierenden Signale abgelegt sind. In diesem Fall müssen die Zeilenanzahlen von Signal1 und Signal2 übereinstimmen.
Die nicht-zirkuläre Faltung basiert auf der Annahme, dass die Signale außerhalb der durch die Datensätze Signal1 und Signal2 abgedeckten Ausschnitte den Betrag Null haben. Vor dem Übergang in den Frequenzbereich wird deshalb eine ausreichende Anzahl von Nullen an die Datensätze angehängt. Das Faltungsprodukt wird für alle τ berechnet, für die dieses einen Wert ungleich 0 haben kann, d. h. für die noch eine Überlappung der beiden Signale vorliegt.
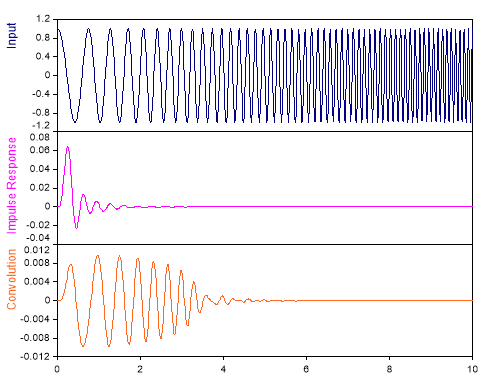
Folgende Grafik zeigt die Faltung eines Wobbelkosinussignals mit der Impulsantwort eines Tiefpassfilters für alle positiven τ:
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
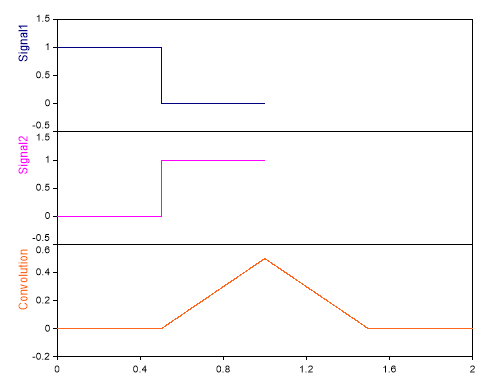
Dim Signal1 = Signal(0.5 * Square(2. * PI * 1.0 * (1000, 0.0, 0.001), 0.5) + 0.5, (1000, 0.0, 0.001))
Dim Signal2 = Signal(0.5 * Square(2. * PI * 1.0 * ((1000, 0.0, 0.001) + 0.5), 0.5) + 0.5, (1000, 0.0, 0.001))
Convolution(Signal1, Signal2, CONVOLUTION_NONCIRCULAR)
Nicht-zirkuläres Faltungsprodukt zweier Rechtecksignale.
Siehe auch
Literatur
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition", Seite 570 - 73. "Prentice Hall, New Jersey",1999.ISBN 0-13-754920-2.
[2] "H. D. Lüke": "Signalübertragung", Seite 79 - 81. "Springer-Verlag Berlin, Heidelberg, New York",1985.ISBN 3-540-15526-0.
