Kontinuierliche Wavelet Transformation (CWT)
Die Kontinuierliche Wavelet Transformation (CWT = Continuous Wavelet Transform) wird verwendet, um ein Signal in Wavelets zu zerlegen. Wavelets sind Oszillationen, die in einem kurzen Zeitausschnitt auftreten. Während die Fourier-Transformation ein Signal in zeitlich unbeschränkte Sinus- und Kosinusschwingungen zerlegt und dabei jegliche Information zur Zeitlokalisierung verliert, sind die Elementarfunktionen der CWT skalierte und verschobene Versionen des zeit-lokalen Mutter-Wavelets. Die CWT wird zur Erstellung einer Zeit-Frequenz-Repräsentation des Signals verwendet, die eine hohe Zeit und Frequenz-Auflösung aufweist.
Die CWT ist ein exzellentes Werkzeug zur Abbildung der sich ändernden Eigenschaften nicht-stationärer Signale. Sie ist ebenfalls gut geeignet, um die Stationariät zu überprüfen. Wenn ein Signal sich als nicht-stationär erweist, dann kann die CWT dazu verwendet werden, stationäre Teilstücke des Signals aufzuspüren.
Die grundlegenden Berechnungen in den CWT-Prozeduren von FlexPro folgen den Algorithmen von Torrence und Compo. Die Nomenklatur der folgenden Gleichungen entspricht ebenfalls der unten aufgeführten Publikation von Torrence und Compo.
Kontinuierliche Wavelet Transformation
Die CWT basiert auf folgenden Definitionen:
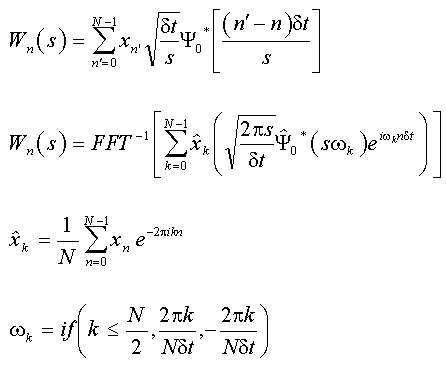
Die CWT ist eine Faltung der Datenreihe mit einer skalierten und verschobenen Version des Mutter-Wavelets, der Ψ-Funktion. Diese Faltung kann entweder direkt, wie in der ersten Gleichung angegeben, oder über eine FFT-basierte schnelle Faltung, wie in der zweiten Gleichung angegeben, berechnet werden.
Beachten Sie, dass die CWT eine kontinuierliche Funktion ist mit Ausnahme der diskreten Datenreihe x und deren diskreter Fourier-Transformation. In diesen Gleichungen symbolisiert * eine komplexe Konjugation, N ist die Länge der Datenreihe, s ist der Skalierungsfaktor für das Wavelet, δt ist das Abtastintervall, n ist der lokalisierte Zeitindex und ω ist die Kreisfrequenz. Jede der Gleichungen umfasst eine Normierung, so dass das Wavelet die gleiche Energie bei jeder Skalierung aufweist.
Bei der CWT wird für jeden gewählten Skalierungsfaktor die Korrelation zwischen dem Wavelet und aufeinander folgenden Segmenten der Datenreihe berechnet. Solange keine Rekonstruktion erforderlich ist, gibt es keinerlei Beschränkungen für die Anzahl der Skalierungsfaktoren und deren Schrittweite. Ein CWT-Spektrum kann eine lineare oder logarithmische Skalierung bei jeder gewünschten Dichte verwenden. Wenn dies gewünscht wird, kann ein hochauflösendes Spektrum für einen engen Frequenzbereich berechnet werden. Die Faltungen können bis zu N-mal für jede Skalierung berechnet werden und sie müssen für alle N berechnet werden, wenn eine FFT verwendet wird. Die CWT besteht aus N Spektralwerten für jeden verwendeten Skalierungswert und jeder davon erfordert eine inverse FFT. Der Berechnungsaufwand und auch der Speicherbedarf sind dadurch erheblich. Der Vorteil dieser hohen Redundanz in der CWT ist ein genaues Zeit-Frequenz-Spektrum.
Wavelet Elementarfunktionen (Mutter-Wavelets)
Anders als die Fourier-Zerlegung, welche komplexe Exponentialfunktionen als Elementarfunktionen verwendet, werden bei der Wavelet-Zerlegung zeitlokale Mutter-Wavelets eingesetzt. Die Mutter-Wavelet-Funktion ist kontinuierlich sowohl in der Zeit als auch in der Frequenz und dient als Ausgangsfunktion für die Konstruktion der skalierten und verschobenen Elementarfunktionen. Das Mutter-Wavelet kann komplex oder reell sein und weist in jedem Fall einen Anpassungsparameter auf, mit der die Eigenschaften der Schwingung eingestellt werden können. Die Wavelet-Analyse ist schwieriger als die Fourier-Analyse, da das Mutter-Wavelet, aus dem die Elementarfunktionen konstruiert werden, zunächst festgelegt werden muss. FlexPro bietet drei verschiedene Mutter-Wavelets, jedes in einer komplexen und einer reellen Version.
Morlet-Wavelet
Das am häufigsten verwendete Wavelet ist das Morlet-Wavelet, eine Gauß-bewertete komplexe Sinusschwingung, welche wie folgt im Zeit- und Frequenzbereich definiert ist:
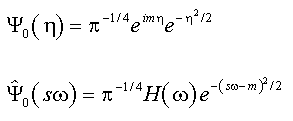
In diesen Gleichungen ist η ein dimensionsloser Zeitparameter, m ist die Wellenzahl und H die Heaviside-Funktion.
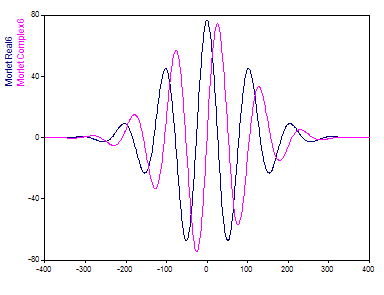
Die folgende Zeitbereichsdarstellung zeigt den Realteil und den Imaginärteil eines Morlet-Wavelets mit einem Anpassungsparameter (Wellenzahl) von 6:
Der Anpassungsparameter des Morlet-Wavelets, die Wellenzahl, kann in FlexPro von 6 bis 100 variieren. Eine Wellenzahl von 20 führt zu folgender Darstellung im Zeitbereich:
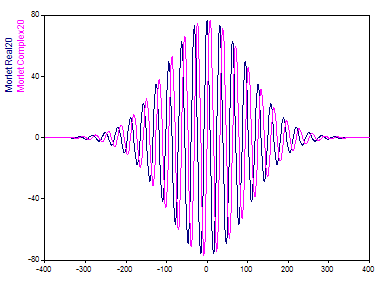
Die Anzahl der Oszillationen im Morlet-Wavelet entspricht in etwa der Wellenzahl.
Paul-Wavelet
FlexPro bietet auch das Paul-Wavelet an:
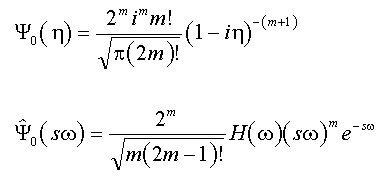
Das Paul-Wavelet klingt schneller ab. Der Anpassungsparameter des Paul-Wavelets ist eine Ordnung, die für FlexPro im Bereich von 4 bis 40 angegeben werden kann. Bei einer Ordnung von 4 existiert nur eine Schwingung im Wavelet:
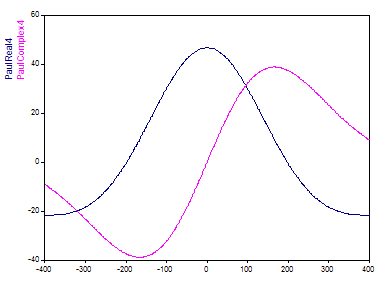
Sogar bei der höchsten verfügbaren Ordnung von 40, zeigt das Paul-Wavelet nur eine Anzahl von Oszillationen, die der geringsten Wellenzahl des Morlet-Wavelets entspricht:
Das Paul-Wavelet bietet eine bessere Zeitlokalisierung als das Morlet-Wavelet, da es im Zeitbereich schneller abklingt. Anders als das Morlet-Wavelet ist seine Darstellung im Frequenzbereich kein symmetrischer Peak sondern einer, der nach rechts in Richtung höherer Frequenzen verschoben ist. Es ähnelt einem Gamma-Peak und die Schiefe nimmt mit höherer Ordnung ab. Doch sogar bei der höchsten verfügbaren Ordnung von 40 zeigt es eine deutliche Schiefe des Haupt-Peaks im Frequenzbereich. Das Paul-Wavelet bietet dadurch eine geringere Frequenzauflösung.
Gaussian-Derivative-Wavelet
Das dritte von FlexPro unterstützte Wavelet ist das Gaussian-Derivative-Wavelet. Der Realteil ist wie folgt definiert:
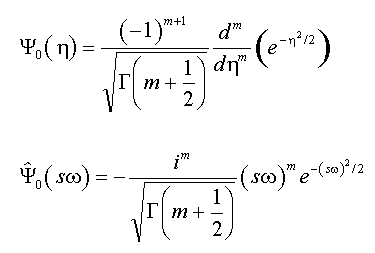
Das komplexe Wavelet entsteht durch die Addition einer Heaviside-Funktion im Frequenzbereich. Dieses Wavelet klingt mit der Quadratwurzel der Gamma-Funktion ab. Seine Zeitlokalisierung liegt zwischen der des Morlet- und des Paul-Wavelets. Der Anpassungsparameter ist die Ordnung der Ableitung und kann in FlexPro von 2 bis 80 variiert werden. Die kleinste Ableitung von 2 ist als das "Marr"- oder "Mexican Hat"-Wavelet bekannt. Das Wavelet enthält eine einzige Schwingung:
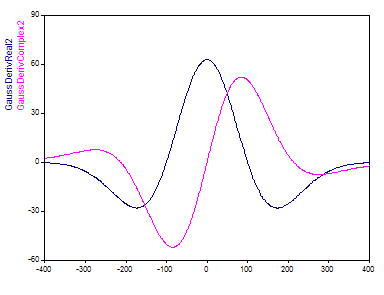
Beim größten Anpassungsparameter von 80 enthält das Gaussian-Derivative-Wavelet etwa so viele Oszillationen wie das Morlet-Wavelet bei einer Wellenzahl von 12:
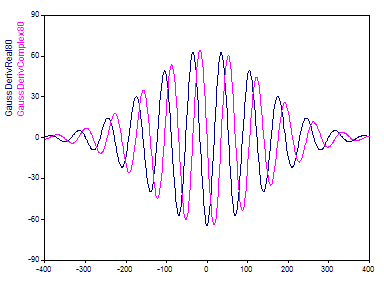
Darstellung im Frequenzbereich
Die Transformationen in den Frequenzbereich der Mutter-Wavelets (Morlet mit Wellenzahl 6, Paul mit Ordnung 40 und Gaussian-Derivative mit Ordnung 20) ergibt folgende Darstellung:
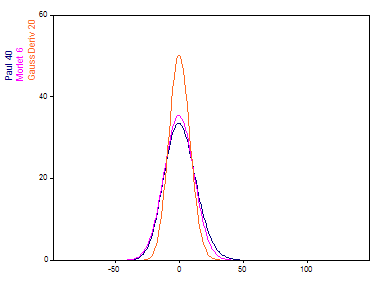
Wenn man den Anpassungsparameter für alle drei Wavelets so einstellt, dass diese ca. sechs Oszillationen enthalten, dann zeigt das Gaussian-Derivative-Wavelet die kompakteste Frequenz-Darstellung. Das Paul-Wavelet zeigt den breitesten Peak und das Morlet-Wavelet liegt dazwischen.
Die Fourier-Transformation eines Morlet-Wavelets erzeugt einen symmetrischen Peak, die Spektraldarstellung des Gaussian-Derivative-Wavelets ist ein exakter Gamma-Peak und die Schiefe nach rechts ist deutlich geringer als die des Paul-Wavelets und verschwindet nahezu für eine Ableitungsordnung größer als 20. (Höhere Werte für die Ableitung des Gaussian-Derivative-Wavelets zeigen nahezu Gauß-förmige Spektralpeaks.)
Zeitauflösung im Vergleich zur Frequenzauflösung
Alle drei Mutter-Wavelets weisen durch schnelles Abklingen eine sehr gute Zeitlokalisierung der Oszillation auf. Für eine gegeben Anzahl von Oszillationen, lokalisiert das Paul-Wavelet am effektivsten im Zeitbereich. Das Morlet-Wavelet ist etwas weniger effizient und das Gaussian-Derivative-Wavelet zeigt die geringste Zeitlokalisierung der drei auf. Beim Vergleich der Frequenzauflösungen schneidet jedoch das Gaussian-Derivative-Wavelet am besten und das Paul-Wavelet am schlechtesten ab. Das Morlet-Wavelet liegt auch hier dazwischen.
Obwohl das Morlet-Wavelet für eine gegebene Anzahl von Oszillation nicht so kompakt ist wie das Gaussian-Derivative, kann eine viel größere Anzahl von Oszillationen eingestellt werden. Dadurch kann mit dem Morlet-Wavelet eine größere Frequenzauflösung erzielt werden.
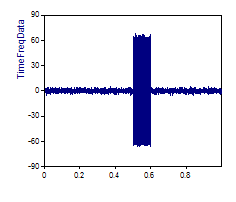
Dies lässt sich am besten Graphisch darstellen. Die folgenden Wavelet-Analysen verwenden einen verrauschten Datensatz, bei dem eine einfache Sinusschwingung im Zeitbereich von 0,5 bis 0,6 auftritt:
Die Spitze des Peaks wurde vergrößert, so dass der Kompromiss in der Zeit-Frequenz-Auflösung deutlich wird. Alle Grafiken verwenden die gleiche Skalierung für die Zeit und die Frequenzachse. Für die ersten drei Bilder wurde ein Morlet-Wavelet mit den Wellenzahlen 6, 20 und 50 verwendet:
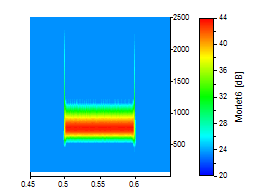
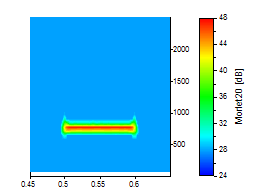
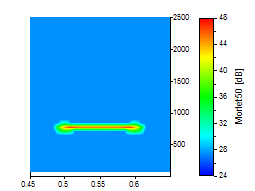
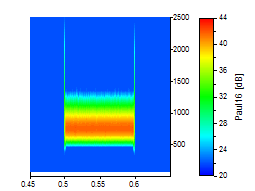
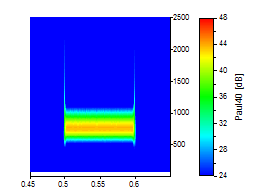
Für die nächsten drei Bilder wurde ein Paul-Wavelet mit den Ordnungen von 4, 16 und 40 eingesetzt:
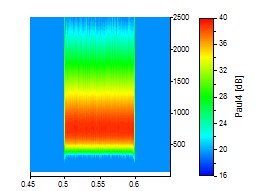
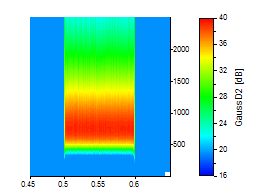
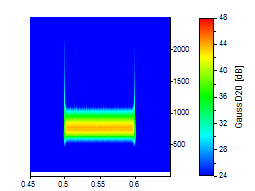
Für die letzten drei Bilder wurde ein Gaussian-Derivative-Wavelet mit den Ordnungen 2, 20 und 80 gewählt:
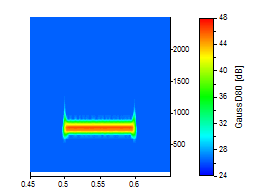
Wenn keine optimale Zeitauflösung benötigt wird, ist das Morlet-Wavelet im Allgemeinen eine gute Wahl, da es eine gut Auflösung sowohl für die Frequenz als auch die Zeit liefert.
Die Frequenzauflösung des Paul-Wavelet mit höchster Ordnung 40 entspricht etwa dem Morlet-Wavelet mit dessen niedrigster Wellenzahl von 6. Bei den Beispielen zum Paul-Wavelet können Sie auch die Asymmetrie in der Frequenz erkennen. Wenn Sie jedoch an einer optimalen Zeitauflösung interessiert sind, ist das Paul-Wavelet eine gute Wahl.
Das Gaussian-Derivative-Wavelet kommt bei seiner höchsten Frequenzauflösung (Ordnung 80) dem Morlet-Wavelet mit einer Wellenzahl von 12 nahe. Anders als beim Paul-Wavelet sind höhere Ordnungen fast symmetrisch und die Frequenzauflösung kann die des Morlet-Wavelet bei niedrigen Wellenzahlen übersteigen.
"Multiresolution"-Analyse
Bei der Kurzzeit-Fourier-Transformation steuert die feste Segmentlänge das Verhältnis von Zeit- und Frequenzauflösung. Dies führt zu einer konstanten Zeit- und Frequenzauflösung, die unabhängig von der darzustellenden Frequenz ist. Im Gegensatz hierzu ist die CWT eine Analyse mit variabler Auflösung. Diese "Multiresolution"-Analyse wurde für den häufigen Fall entwickelt, wo Signalanteile mit hoher Frequenz nur für kurze Zeiten existieren, während niederfrequente Anteile persistenter sind.
Kurzlebige hochfrequente Anteile benötigen eine gute Zeitlokalisierung. Um dies zu erreichen, wird die Frequenzauflösung herab gesetzt. Andererseits tolerieren langlebige Anteile niederer Frequenz eine geringere Zeitauflösung, benötigen jedoch eine höhere Frequenzauflösung. Niederfrequente Spektralkomponenten bilden oft den größten Anteil im Signal und werden am besten quantifiziert, wenn die Frequenzauflösung so hoch wie möglich ist.
Bei der Multiresolution-Analyse wird das schwierige Problem der optimalen Segmentlänge umgangen. Die Breite der Zeitsegmente variiert automatisch mit der Frequenz. Dies ist jedoch offensichtlich ein Nachteil, wenn ein Signal kurzlebige Anteile niedriger Frequenz aufweist. Für solche Signale ist die Kurzzeit-Fourier-Transformation oft die bessere Wahl. Auch macht es diese Variation der Frequenzauflösung unmöglich, die spektralen Leistungen oder Amplituden direkt aus dem Wavelet-Spektrum auszulesen. Auch hier hat die STFT Vorteile gegenüber der CWT.
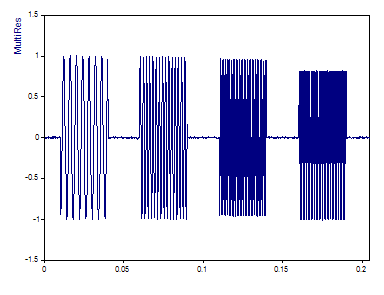
Der folgende Datensatz enthält eine Sequenz von Sinusschwingungen gleicher Leistung bei 1% Rauschen. Im Zeitbereich von 0,01 bis 0,04 liegt eine Frequenz von 250Hz vor, von 0,06 bis 0,09 eine Frequenz von 500 Hz, von 0,11 bis 0,14 eine Frequenz von 1KHz und im Bereich von 0,16 bis 0,19 eine von 2Khz.
Im folgenden Spektrum wurde ein Morlet-Wavelet mit einer Wellenzahl von 12 verwendet:
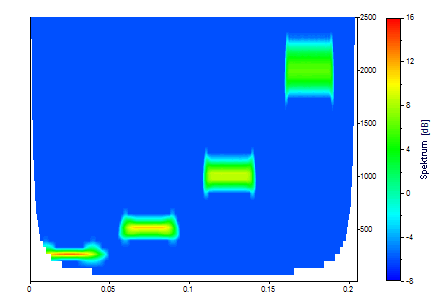
Die variable Auflösung ist deutlich erkennbar. Die 250Hz Komponente ist sehr gut in der Frequenz aufgelöst aber sehr unscharf in der Zeit. Umgekehrt ist die 2000Hz Komponente in der Zeit scharf abgebildet, weist aber eine Unschärfe in der Frequenz auf.
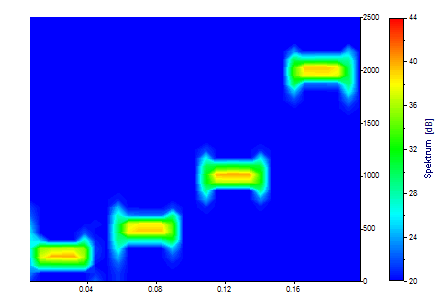
Hier im Vergleich dazu eine optimierte STFT. Die feste Auflösung des STFT ist klar ersichtlich:
Anhängen von Nullen und der "Cone of Influence"
Bei der Berechnung des CWT-Spektrums wird zunächst eine FFT der Datenreihe berechnet. Dann wird für jede Skalierung (gewünschte Frequenz) im Spektrum die Frequenzantwort des Wavelet berechnet und mit dem Spektrum des Datensatzes multipliziert. Das Produkt wird dann rücktransformiert.
Fourier-Transformationen bedingen periodische Daten. Damit die schnelle Faltung über FFT keine Spiegelungseffekte aufweist, welche durch Nichtperiodizität in der Datenreihe oder der Antwort-Funktion (Tochter-Wavelet) verursacht werden, müssen Nullen in einer Anzahl angehängt werden, die mindestens der Hälfte der Anzahl der von Null verschiedenen Werte in der Frequenzantwort des Tochter-Wavelets entspricht.
Diese Anzahl hängt von der Skalierung und damit von der Frequenz ab. Anhängen von Nullen auf die doppelte Datensatzgröße stellt sicher, dass nirgendwo im Spektrum Spiegelungseffekte auftreten können. Oft ist es möglich, auf die nächste 2er-Potenz zu verlängern und damit vernachlässigbare Spiegelungseffekte bei optimaler Performance der FFT zu erreichen.
Werden genügend Nullen angehängt, dann werden zwar die Spiegelungseffekte beseitigt, aber es treten andere Effekte auf. Durch das Anhängen der Nullen wird mit hoher Wahrscheinlichkeit eine Diskontinuität am Ende des Datenstroms erzeugt. Des Weiteren wird die Leistung im Bereich der Ränder des Spektrums durch das Einfügen von Nullen in die Faltung verringert.
Diese Zone mit Randeffekten wird als "Cone Of Influence" (COI) bezeichnet. In FlexPro wird in diesem Bereich keine Spektralinformation angezeigt. Die Spektralinformation im Cone of Influence ist wahrscheinlich ungenau, unabhängig davon, ob Nullen angehängt wurden oder nicht. Wenn keine Nullen angehängt wurden, können dort Spiegelungseffekte auftreten. Wurden Nullen angehängt, können die Leistungen vermindert sein.
Der Cone of Influence wird berechnet, wie in dem Artikel von Torrence und Compo beschrieben.
Orthogonale Wavelets und die DWT
Die meisten Wavelet-Analysen verwenden ein Filterpaar, um die nieder- und hochfrequenten Anteile in einem Signal sukzessive zu isolieren. Dies ist als Diskrete Wavelet-Transformation (DWT = Discrete Wavelet Transform) bekannt. Die DWT-Wavelets sind keine kontinuierlichen Funktionen der Zeit und ihre Transformationen sind keine kontinuierlichen Funktionen der Frequenz. Stattdessen handelt sich um Mengen von Zeitbereichs-Filterkoeffizienten, die eine orthogonale Basis erzeugen, welche die Filterung und Rekonstruktion der Daten erleichtert. Eine DWT weist keine Redundanz auf. Die Anzahl der Blöcke von Wavelet-Leistungen für jede Skalierung ist eine Funktion der nicht-überlappenden Wavelet-Breite. In einer typischen DWT wird die Frequenz in ganzzahligen Potenzen von Zwei geteilt und die Anzahl der Blöcke pro Zeiteinheit nimmt ebenfalls um Zweierpotenzen mit dieser Frequenz zu. Obwohl die DFT schnell ist und deren Zeit-Frequenz-Darstellung nur wenig Speicher benötigt, ist sie doch für die Spektralanalyse im Zeit-Frequenzbereich ungeeignet.
FlexPro verwendet ausschließlich die CWT zur Spektralanalyse im Zeit-Frequenzbereich. Der CWT-Algorithmus bietet größere Genauigkeit, die jedoch mit hohem Berechnungsaufwand und Speicherbedarf einhergeht.
Literatur
Falls Sie die Feinheiten näher kennen lernen möchten, die bei der Anwendung der CWT auf reale Daten zu beachten sind, dann ist der folgende Artikel eine kompakte und gut verständliche Quelle:
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, v.79, no.1, p.61-78. January 1998
Diese Referenz beschreibt die CWT im Kontext der Auswertung von El Nino Zeitreihen. Die Autoren haben auch ein FORTRAN Programm zur Wavelet-Analyse mit Namen WAVEPACK veröffentlicht. Es ist im Internet unter folgender Adresse verfügbar: http://paos.colorado.edu/research/wavelets/
Siehe auch
Analyseobjekt Zeit-Frequenz Spektralanalyse - Kontinuierliche Wavelet Transformation (CWT) Spektrum