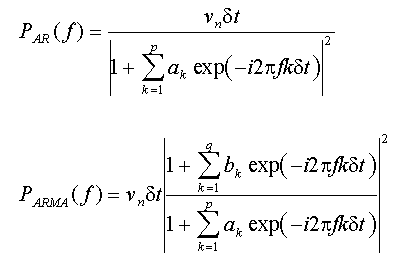Autoregressive Modellierung
Autoregression
Wenn ein Modell erfolgreich an die Daten approximiert werden kann, dann kann dieses Modell statt der ihm zugrunde liegenden Daten in den Frequenzbereich transformiert werden. Das transformierte Modell beschreibt dann ein stetiges und kontinuierliches Spektrum. Dies ist das Grundprinzip für alle durch autoregressive Modellierung erzeugten Spektren. Bei einem AR-Modell basiert ein Wert zu einem Zeitpunkt t auf einer Linearkombination vorhergehender Werte (Vorwärts-Prädiktion) oder auf einer Linearkombination nachfolgender Werte (Rückwärts-Prädiktion) oder aus einer Kombination von beiden (Vorwärts-Rückwärts-Prädiktion). Die linearen Modelle ermöglichen eine stabile und genaue Berechnung.
Definition des AR- und ARMA-Modells
Um die Anzahl der Freiheitsgrade für statistische Tests zu erhalten und um eine gemeinsame Grundlage für alle AR-Algorithmen zu schaffen, ist ein AR-Modell in FlexPro wie folgt definiert:
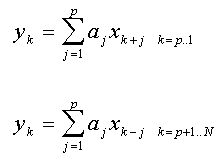
In diese Gleichungen ist x die Datenreihe der Länge N und a ist die Reihe der autoregressiven Parameter der Ordnung p. FlexPro verwendet die positive Vorzeichenkonvention (lineare Prädiktion) für die AR-Koeffizienten. Das Modell ist als Rückwärts-Prädiktion für die ersten p Werte und als Vorwärts-Prädiktion für die restlichen N - p Werte definiert. Diese Definition wird bei jeder Approximationsstatistik verwendet, obgleich dieses Modell von keinem der Kleinste-Quadrate AR-Algorithmen approximiert wird. Das Modell wird nur in dem Fall einer reinen AR-Approximation mittels der ARMA-Prozedur verwendet.
Die ARMA-Definition erhält in gleicher Weise die Anzahl der Freiheitsgrade:
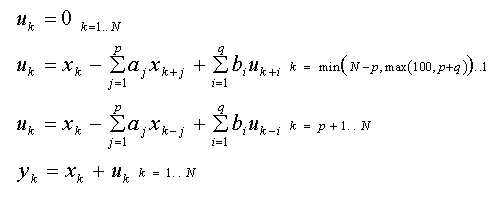
Hier ist b die Reihe der Gleitenden-Mittelwert-Koeffizienten der Ordnung q. Die Berechnungen beginnen auch hier mit einer Rückwärts-Prädiktion, es wird jedoch ein höherer Startindex verwendet, um den gleitenden Mittelwert für die ersten p Werte zu integrieren. Dieses Modell wird von den nicht-linearen ARMA-Algorithmen approximiert.
AR Spektraldefinitionen
Die AR und ARMA spektralen Leistungsdichten sind wie folgt definiert:
In diesen Gleichungen ist ν die Varianz des Weißen Rauschens und δt ist das Abtastintervall. Bitte beachten Sie, dass beide Spektralmodelle kontinuierliche Funktionen der Frequenz sind.
Klassifikation der AR-Algorithmen
Die AR-Koeffizienten können auf verschiedene Weisen berechnet werden. Sie können von Schätzungen der Autokorrelation, aus den partiellen Autokorrelationskoeffizienten und über Kleinste-Quadrate-Algorithmen berechnet werden. Bei der Berechnung des AR-Modells über die Korrelationsmethode hängt das Ergebnis von der maximalen Verzögerung (maximum lag) ab, für die die Autokorrelation berechnet wird. Bei der partiellen Autokorrelationsmethode hängt des von der spezifischen Definition des Reflexionskoeffizienten ab. Bei den Kleinste-Quadrate-Methoden hängt das Ergebnis davon ab, wie die Daten an den Rändern behandelt werden und ob die Datenmatrix oder die Normalengleichungen approximiert werden.
Die meisten AR-Algorithmen in FlexPro sind Kleinste-Quadrate-Prozeduren, da diese die besten Spektralschätzungen erzeugen. Die Kleinste-Quadrate-Algorithmen mit integrierter Separation von Signal und Rauschen mittels Singulärwertzerlegung (SVD=Singular Value Decomposition) sind die stabilsten von FlexPro's AR-Methoden. Diese Algorithmen sind in die AR-Spektralschätzer fest integriert.
AR-Prädiktionsmodelle
Eine kontinuierliche Funktion der Zeit benötigt nur die berechneten Parameter, um für jeden beliebigen Zeitwert einen Funktionswert berechnen zu können. Ob das ursprüngliche Abtastintervall konstant oder variabel war, spielt keine Rolle mehr, sobald das Modell approximiert ist. Dies trifft für ein Autoregressives Modell nicht zu. Ein lineares AR-Prädiktionsmodell ist eine diskrete Funktion, welche konstant abgetastete Daten erfordert.
Wenn ein AR-Modell im Zeitbereich für einen nächsten Wert ausgewertet wird, dann wird ein Teil der vorhergehenden Datensequenz mittels der AR-Koeffizienten gefiltert, um das neue Element zu erzeugen. Obwohl ein lineares AR-Modell keine explizite Rausch-Komponente hat, ist dies doch Teil der Datensequenz. Weißes Rauschen wird dadurch, unter der Annahme dass es unkorreliert ist, von Punkt zu Punkt gehandhabt.
Limitierungen des AR Modells
In der Praxis ist es oft nicht möglich, einen Wert basierend auf dessen Vorgängern vorherzusagen. Der Prozess kann z. B. stochastisch (zufällig) statt deterministisch sein bzw. keine Korrelation zwischen dem Wert und seinen Vorgängern bestehen.
Auch ist das Hintergrundrauschen nicht zwingend weiß und unkorreliert. Geophysikalische Prozesse haben z. B. oft einen Hintergrund mit rotem Rauschen. Bei rotem Rauschen sinkt die Varianz mit höherer Frequenz. In einigen Fällen kann der Trend im Rauschen als AR-Modell erster Ordnung approximiert werden.
Je höher die Ordnung eines AR-Modells, desto mehr Komponenten der Datenreihe können modelliert werden. Wenn kein Rauschen vorhanden ist, werden harmonische Komponenten (sinusförmige Funktion) mit einer Ordnung erfasst, die dem Doppelten ihrer Anzahl entspricht. Häufig ist, jedoch auch Rauschen vorhanden.
Des Weiteren sind Schmalband-Komponenten oft nicht exakt harmonisch. Dies kann näherungsweise zutreffen, das heißt, es treten zwar regelmäßige Oszillationen auf, die jedoch nicht mit einer einzigen sinusförmigen oder gedämpft-sinusförmigen Funktion beschrieben werden können. Die Information, die zur Beschreibung solcher Oszillationen nötig ist, kann von einem AR-Modell u. U. erst durch Erfassung einer großen Anzahl von Zyklen der Schwingung erfasst werden. Für langsam veränderliche Strukturen kann dies eine hohe Modellordnung erfordern.
AR Signal-Rauschen-Separation
Eine einfache AR-Approximation bietet keine effektive Trennung von Signal und Rauschen. Sogar wenn reine Sinusschwingungen in nur geringem Rauschen eingebettet sind, wird oft eine Ordnung weit höher als dem Doppelten der Komponentenanzahl benötigt, um diese Schwingungen erfassen und spektral abbilden zu können. In anderen Worten, wenn die Ordnung zu klein ist, dann wird nur ein Teil des deterministischen Signals erfasst und der Rest wird als Rauschen interpretiert. Es gehen also Spektralkomponenten verloren.
Wenn andererseits die Ordnung zu hoch ist, dann wird zwar das deterministische Signal vollständig erfasst, aber ein Teil des Rauschens wird ebenfalls modelliert. Im Spektrum können dann zusätzliche kleine Peaks auftauchen.
Es gibt drei Möglichkeiten, diese Beschränkungen zu behandeln. Erstens kann das Rauschen vor der Analyse gefiltert werden. Zweitens kann eine optimale Modellordnung ermittelt werden, die alle Signalkomponenten erfasst, aber so wenig Rauschen wie möglich abbildet. Die dritte Möglichkeit ist eine integrierte Rauschunterdrückung durch die Kleinste-Quadrate-Algorithmen, die die Koeffizienten berechnen. Diese letzte Alternative wird empfohlen.
Auswahl der Signal-Eigenmoden
Statt zu versuchen, eine optimale Modellordnung zu finden, kann eine explizite Trennung von Signal und Rauschen durchgeführt werden. Mit wachsender Ordnung steht eine wachsende Anzahl von Koeffizienten zur Abbildung von Signal und Rauschen zur Verfügung. Wenn ein Matrix-Algorithmus basierend auf Hauptkomponenten verwendet wird, dann beschreiben die ersten Eigenvektoren die Signalkomponenten und die nachfolgenden das Rauschen. Die Modellordnung ist dann weniger wichtig, da die dem Rauschen zugeordneten Vektoren bei der Berechnung der AR-Koeffizienten nicht berücksichtigt werden.
Diese integrierte Trennung von Signal und Rauschen wird durch Singulärwertzerlegung (SVD) in den Kleinste-Quadrate-Algorithmen erreicht. Diese Option wird in allen AR und ARMA-Algorithmen mit SVD verwendet. Die erhaltenen Eigenmoden sollten dabei das Signal bzw. die Hauptkomponenten repräsentieren, da diese zum Ergebnis der Berechnung beitragen. Die verworfenen Eigenmoden sollten ausschließlich Rauschen zugeordnet sein, da diese entfernt werden und keinen Beitrag zum Ergebnis leisten. Diese Trennung von Rauschen und Signal ist ein integraler Bestandteil der SVD-Prozeduren. Für die Analyse von Schmalband-Komponenten werden zwei Signal-Eigenmoden pro Komponente benötigt. Für ein Signal mit z. B. drei Spektralkomponenten muss der Signalunterraum daher auf sechs gesetzt werden.
Kontinuierliche AR-Spektren
Die AR-Frequenzspektren umfassen keine Filterung der Datensequenz mit Ausnahme der Ermittlung eines globalen Maßes für das weiße Rauschen. Aus diesem Grund sind die AR-Spektren so glatt. Die AR-Koeffizienten modellieren nur deterministische Komponenten, während das Rauschen als Konstante erfasst wird, die der Varianz des weißen Rauschens bzw. dem Residuum der Approximation entspricht. Die AR-Frequenztransformation verwendet nur die AR-Koeffizienten und diese Varianz des weißen Rauschens. Das Ergebnis ist eine kontinuierliche Funktion der Frequenz.
Jede der FlexPro AR-Algorithmen erzeugt eine Schätzung des weißen Rauschens. Diese Varianz beeinflusst die Höhe aber nicht die Form oder die Frequenz der spektralen Peaks. Fehler bei der Schätzung dieser Varianz des Rauschens fließen als Amplitudenfehler in das AR-Spektrum ein. Die Burg und Autokorrelations-Algorithmen erzeugen in der Regel normalverteilte Vorhersagefehler und AR-Spektren, deren Integral sehr nahe bei der Signalleistung liegt. Für die Kleinste-Quadrate-Algorithmen trifft dies u. U. nicht zu.
Eine erfolgreiche Approximation eines AR-Modells an die Signalkomponenten kann oft schon mit sehr kleinen Datensätzen erreicht werden und man erhält ein sehr hoch auflösendes Spektrum. Ein AR-Spektralschätzer zeigt oft beeindruckend scharfe Peaks und diese liegen sehr dicht bei der exakten Frequenz der vorhandenen Spektralkomponenten. In einem AR-Model werden die Frequenzen direkt aus den Wurzeln des Modells ermittelt. Es wird daher keine Suche nach lokalen Maxima im Spektrum benötigt.
Wenn man die AR-Methoden mit der FFT vergleicht, erkennt man, dass die FFT in vieler Hinsicht einfacher zu handhaben ist. Eine FFT erfordert zwar einige Optimierungen, wie z. B. die Wahl eines geeigneten Fensters, der Segmentlänge und Überlappung oder der Anzahl der anzuhängenden Nullen, aber es ist schwierig, ein total falsches Ergebnis zu erzeugen. Auch sind die Auswirkungen der einzelnen Parameter der FFT-Algorithmen recht intuitiv. Dies trifft für AR-Spektren nicht immer zu.
Siehe auch
Analyseobjekt Spektralschätzer - AR-Spektralschätzer