Calcule les coefficients du numérateur et du dénominateur d'un filtre notch IIR du deuxième ordre qui peut être utilisé pour filtrer les fréquences dans une gamme de fréquences étroite (filtre coupe-bande à bande étroite).
Syntaxe
IIRNotchFilter(NotchFrequency, le Bandwidth [ , le SamplingRate ])
La syntaxe de la fonction IIRNotchFilter se compose des éléments suivants :
Section |
Description |
|---|---|
NotchFrequency |
Spécifie la fréquence notch du filtre. La fréquence doit être comprise entre 0 et 0,5 (moitié du taux d'échantillonnage normalisé à l'unité) ou entre 0 et 0,5 * SamplingRate. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
Bandwidth |
Spécifie la largeur de bande (disposée symétriquement autour de la fréquence d'encoche) du filtre notch. Elle définit la plage de fréquences dans laquelle les fréquences sont filtrées (définie par le point -3 dB, c'est-à-dire l'endroit où 70,7 % de l'amplitude initiale du signal est atteinte). Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
SamplingRate |
Précise le taux d'échantillonnage. L'argument est facultatif. Si cet argument n'est pas spécifié, la fréquence limite doit être définie comme suit pour NotchFrequency une fréquence normalisée de 0 à 0,5 doit être spécifiée. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure à 0. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
Remarques
Les coefficients du numérateur et du dénominateur du filtre coupe-bande IIR de deuxième ordre sont renvoyés sous forme de liste à deux éléments b et a. Utilisez la fonction Filter pour filtrer les données avec le filtre calculé.
Les filtres à encoches représentent un type de filtre coupe-bande à bande particulièrement étroite qui ne présente qu'un seul point zéro dans la fonction de transfert et qui atténue donc le plus fortement possible non pas une large bande de fréquences, mais idéalement une seule fréquence.
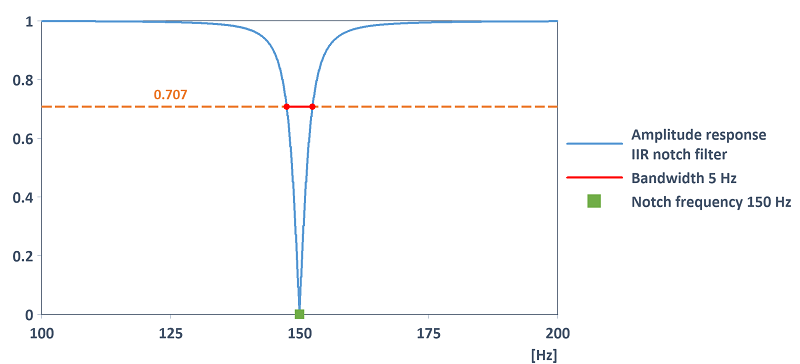
Le filtre a la réponse d'amplitude suivante (ici, par exemple, pour la fréquence notch de 150 Hz et la bande passante de 5 Hz) :
Disponible dans
Option Filtres numériques
Exemples
Dim coeff = IIRNotchFilter(0.2, 0.02)
Filter(Signal, coeff, TRUE)
Les coefficients numérateur et dénominateur du filtre coupe-bande sont d'abord calculés, puis les données sont filtrées avec correction de phase à l'aide de la fonction Filter. Le filtre notch a une fréquence de 0,2 et une largeur de bande de 0,02.
Dim coeff = IIRNotchFilter(100 Hz, 8 Hz, SamplingRate(Signal))
Filter(Signal, coeff, TRUE)
Les coefficients numérateur et dénominateur du filtre coupe-bande sont d'abord calculés, puis les données sont filtrées avec correction de phase à l'aide de la fonction Filter. Le filtre notch a une fréquence de 100 Hz et une largeur de bande de 8 Hz .
Dim coeff = IIRNotchFilter(0.15, 0.02)
AmplitudeResponse(coeff, 100000)
Calculez la réponse en amplitude (avec 100 000 points de données) du filtre coupe-bande pour la fréquence de coupure normalisée 0,15 et la largeur de bande 0,02 à l'aide de la fonction AmplitudeResponse.
Dim coeff = IIRNotchFilter(150 Hz, 5 Hz, 1000 Hz)
AmplitudeResponse(coeff, 500000, 1000 Hz)
Calcule la réponse d'amplitude (avec 500000 points de données) du filtre coupe-bande pour la fréquence notchde 150 Hz et la largeur de bande de 5 Hz (taux d'échantillonnage de 1 kHz) en utilisant la fonction AmplitudeResponse.
Voir aussi
Littérature
[1] Sophocles J. Orfanidis: Introduction to Signal Processing. Prentice Hall, 1996.