Berechnet verschiedene Verteilungs- oder Dichtefunktionen.
Syntax
Distribution(X, Distribution, Parameter1 [ , Parameter2 ])
Die Syntax der Distribution-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
X |
Enthält die X-Werte, d. h. die Werte der Zufallsvariablen, für die die Verteilungsfunktion bzw. die Dichtefunktion berechnet werden soll. Bei Berechnung einer diskreten Verteilung müssen die X-Werte ganzzahlig und positiv sein. Erlaubte Datenstrukturen sind Einzelwert, Datenreihe und Datenmatrix. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||||||||||||||
Distribution |
Gibt an, welche Verteilung berechnet werden soll, und ob die Verteilungs- oder die Dichtefunktion berechnet werden soll. Das Argument Distribution kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||
Parameter1 |
Gibt den ersten Parameter der zu berechnenden Verteilung an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||
Parameter2 |
Gibt, falls benötigt, den zweiten Parameter der zu berechnenden Verteilung an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der Normalverteilung mit Erwartungswert μ und Varianz σ² sind gegeben durch:
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der logarithmischen Normalverteilung mit den Parametern μ und σ² sind gegeben durch:
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der Exponentialverteilung mit dem Parameter α (inverser Skalenparameter) sind gegeben durch:
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der Weibullverteilung mit den Parametern α und β (Formparameter) sind gegeben durch:
Anmerkung: in der Literatur wird statt dem Parameter α häufig auch alternativ die charakteristische Lebensdauer T verwendet (und β mit k bezeichnet). Es gilt hierbei die folgende Relation:
Ebenso wird in der Literatur häufig statt dem Parameter α auch der inverse Skalenparameter λ = 1/T verwendet. Es gilt also:
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der Chi-Quadrat-Verteilung mit dem Parameter n (Anzahl Freiheitsgrade) sind gegeben durch:
P(n1,n2) bezeichnet hier die regularisierte, unvollständige Gammafunktion.
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der Student-t-Verteilung mit dem Parameter n (Anzahl Freiheitsgrade) sind gegeben durch:
I(z,n1,n2) bezeichnet hier (und im Folgenden) die regularisierte, unvollständige Betafunktion.
Die stetige Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) der F-Verteilung (Fisher-Verteilung) mit den Parametern m (Anzahl Freiheitsgrade im Nenner) und n (Anzahl Freiheitsgrade im Zähler) sind gegeben durch:
Die diskrete Wahrscheinlichkeitsdichte f(k) und Verteilungsfunktion F(x) der Binomialverteilung mit den Parametern n (Anzahl Versuche) und p (Erfolgs- oder Trefferwahrscheinlichkeit) sind gegeben durch:
Die diskrete Wahrscheinlichkeitsdichte f(k) und Verteilungsfunktion F(x) der Poissonverteilung mit dem Parameter λ (mittlere Ereignisrate) sind gegeben durch:
Verfügbarkeit
Option Statistik
Beispiele
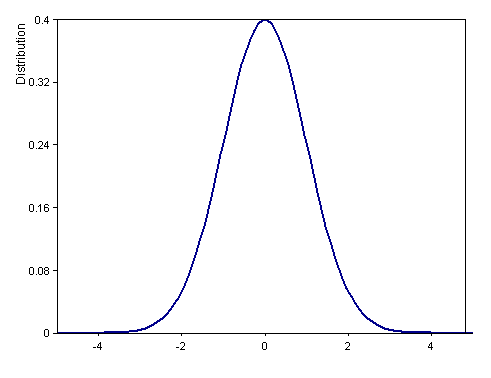
Dim x = Series(-5, 5, 0.05)
Signal(Distribution(x, DISTRIBUTION_NORMAL + DISTRIBUTION_DENSITY, 0, 1), x)
Berechnet die Dichtefunktion der Standardnormalverteilung (Erwartungswert 0, Varianz 1) im Intervall [-5, 5].
Siehe auch
EmpiricalDistribution-Funktion
Literatur
[1] "Hartung, Joachim": "Statistik, 9. Auflage". "Oldenbourg Verlag GmbH, München", 1993. ISBN 3-486-22055-1.