Berechnet die Bessel-Funktion 1. Art mit der angegebenen Ordnung.
Syntax
Jn(n, Number)
Die Syntax der Jn-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
n |
Die Ordnung. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 0 sein. |
Number |
Das Argument für die Funktion. Es sind alle Datenstrukturen erlaubt. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. |
Anmerkungen
Der Datentyp des Ergebnisses ist immer 64-Bit Fließkomma.
Die Struktur des Ergebnisses entspricht der des Arguments Number, ggf. erfolgt die Berechnung elementweise.
Das Ergebnis hat die Einheit 1, sofern Number einheitenbehaftet ist und ansonsten keine Einheit.
Bei zusammengesetzten Datenstrukturen wird nur die Y-Komponente verrechnet.
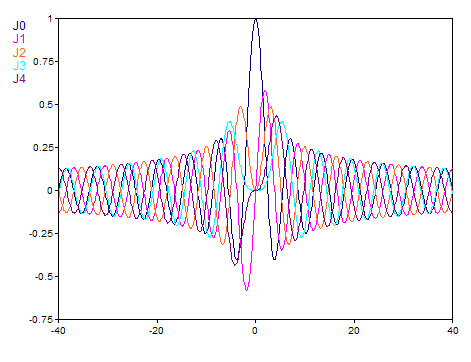
Für ein reelles Argument wird die reelle Bessel-Funktion berechnet. Das Ergebnis hat dann den Datentyp 64-Bit Fließkommazahl. Folgende Grafik zeigt den Verlauf der Funktion für die Ordnungen 0 bis 4 im Intervall [-40, 40]:
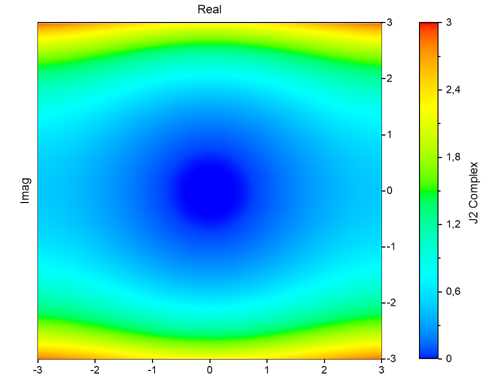
Ist Number komplex, dann wird die komplexe Bessel-Funktion berechnet. Das Ergebnis hat dann den Datentyp komplexe 64-Bit Fließkommazahl. Folgende Grafik zeigt den Betragsverlauf der Funktion für die Ordnung 2:
Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste.
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
Jn(2, 0) |
Ergibt 0. |
Dim x |
Berechnet eine Liste mit drei Signalen mit den Funktionsverläufen der Ordnungen 0, 1 und 2 im Intervall [-40, 40]. |
Siehe auch
Literatur
[1] Donald E. Amos: AMOS - A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order. In: www.netlib.org. https://netlib.org/amos/, 1986.