Cet objet d'analyse vous propose quatre méthodes d'interpolation, c'est-à-dire de lissage, des surfaces.
L'interpolation spline 2D et l'interpolation spline 2D de compensation utilisent les mêmes méthodes mathématiques que l'interpolation spline unidimensionnelle, qui est décrite plus en détail dans cette rubrique. Cependant, dans le cas d'un ensemble de données bidimensionnelles, il s'agit d'une grille de points qui est interpolée successivement dans les directions X et Z. Les données sont ensuite traitées par un logiciel de traitement de données. Vous pouvez régler les conditions limites et le mode d'évaluation séparément pour les deux directions de l'espace.
L'interpolation par spline bicubique interpole la grille de données en une seule étape. Une fonction spline bicubique est utilisée pour chaque "tuile" de la grille de données. La méthode est efficace, robuste et permet d'obtenir des surfaces lisses entre les points de données ainsi qu'au niveau de ceux-ci. Toutefois, aucune condition limite ne peut être fixée.
L'interpolation "Natural Neighbor" est une méthode moderne qui génère des surfaces d'aspect naturel, lisses entre les points de données, mais pas aux points de données. Le résultat ressemble à un tapis de caoutchouc qui a été tiré sur les données. L'algorithme calcule pour chaque point d'échantillonnage une valeur moyenne pondérée sur tous les voisins naturels de ce point.
L'interpolation "Natural Neighbor" est la seule méthode qui vous permette d'interpoler également des données dispersées, c'est-à-dire des données avec des coordonnées X et Z arbitraires. Dans ce cas, les données à interpoler sont une courbe 3D. Si vos données existent sous forme de grille de données, c'est-à-dire sous forme de série de signaux ou de matrice de données, vous pouvez utiliser l'une des trois méthodes d'interpolation.
L'interpolation par "voisin naturel" offre les variantes extrapolant et convexe. En mode extrapolation, tous les points de grille du résultat sont occupés, même pour les courbes 3D qui s'étendent sur une surface convexe, et pour les matrices de données qui ont des valeurs invalides sur les bords. En mode convexe, les points situés à l'extérieur de l'enveloppe convexe sont remplis avec des valeurs invalides.
L'interpolation par spline bicubique et l'interpolation par "voisin naturel" sont directement intégrées dans le graphique de surface 3D de FlexPro, de sorte que vous n'utilisez cet objet d'analyse que lorsque vous souhaitez traiter mathématiquement les données lissées.
L'illustration suivante montre les différents types d'interpolation :
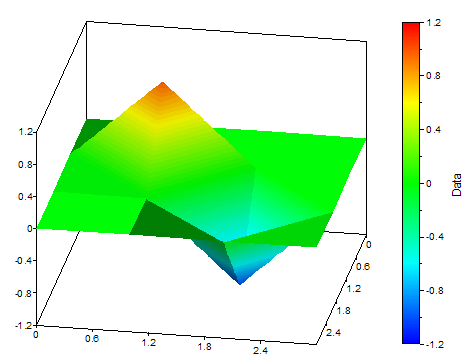
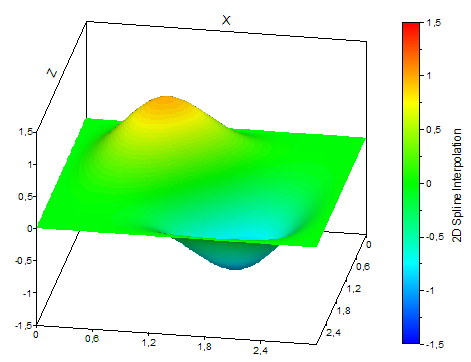
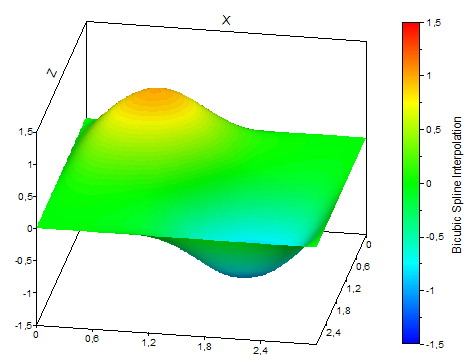
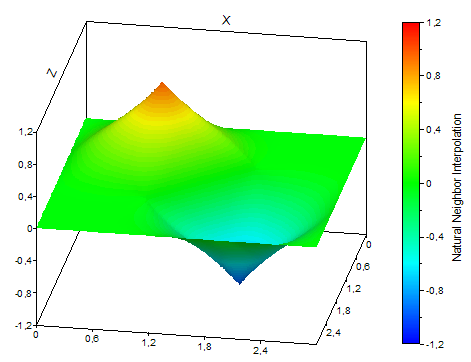
Fonctions FPScript utilisées
Voir aussi
Objet d'analyse Approximation 2D
Objet d'analyse Transformation de courbes
* Cet objet d'analyse n'est pas disponible dans FlexPro View.