Calcule la fonction de Bessel du premier type avec l'ordre spécifié.
Syntaxe
Jn(n, le Number)
La syntaxe de la fonction Jn se compose des éléments suivants :
Section |
Description |
|---|---|
n |
L'ordre. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 0. |
Number |
L'argument pour la fonction. Toutes les structures de données sont autorisées. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. |
Remarques
Le type de données du résultat est toujours Virgule flottante de 64 bits.
La structure du résultat correspond à celle de l'argument Number, si nécessaire, le calcul est effectué élément par élément.
Le résultat a l'unité 1, à condition que Number est unitaire et sinon pas d'unité.
Pour les structures de données composées, seule la composante Y est calculée.
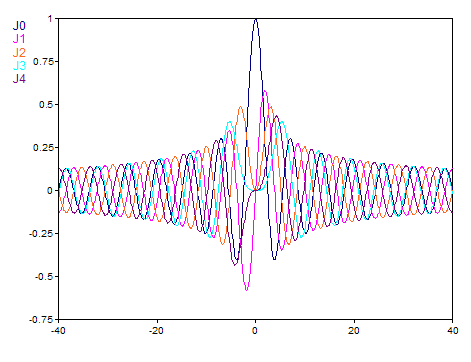
Pour un argument réel, la fonction de Bessel réelle est calculée. Le résultat a alors le type de données valeur à virgule flottante de 64 bits. L'illustration suivante montre la variation de la fonction pour les ordres 0 à 4 dans l'intervalle [-40, 40] :
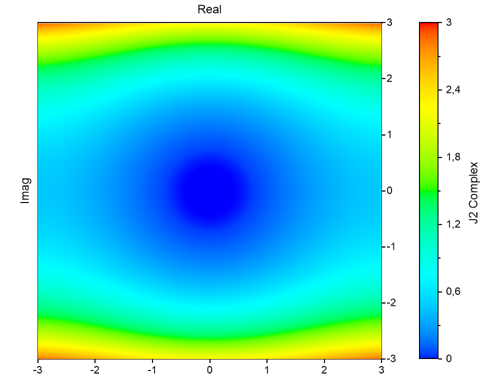
Si est Number complexe, la fonction de Bessel complexe est calculée. Le résultat a alors le type de données valeur complexe à virgule flottante de 64 bits. Le graphique suivant montre l'évolution de l'amplitude de la fonction pour l'ordre 2 :
Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste.
Disponible dans
FlexPro Basic, Professional, Developer Suite
Exemples
Jn(2, 0) |
Renvoie 0. |
Dim x |
Calcule une liste de trois signaux avec les allures des fonctions d'ordre 0, 1 et 2 dans l'intervalle [-40, 40]. |
Voir aussi
Littérature
[1] Donald E. Amos: AMOS - A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order. Dans: www.netlib.org. https://netlib.org/amos/, le 1986.