MeshGrid

Produit une grille bidimensionnelle. Utile pour la visualisation tridimensionnelle de fonctions à deux variables ou de fonctions à arguments à valeur complexe.

Syntaxe

MeshGrid(X, le Z)

La syntaxe de la fonction MeshGrid se compose des éléments suivants :

Remarques

Le résultat a toujours la structure de données Liste.

La fonction crée à partir de deux séries de données X de longueur N et Z de longueur M une liste avec deux entrées de même nom X et Z. Cependant, les entrées de résultats de la liste sont maintenant des matrices composées de N Lignes et de M Colonnes, qui sont créées par réplication des arguments de la fonction X ou . Z sont formées. Les unités des matrices de résultats correspondent aux unités des différents arguments.

Le résultat peut être représenté par une grille rectangulaire bidimensionnelle avec des N x M Points de grille peut être interprété comme suit : Soit par exemple la série de données X comme {1, 2, 3, 4} dans la direction horizontale et la série de données Z comme {7, 8, 9} dans le sens vertical. La grille, tendue par X et Z est maintenant constitué des coordonnées (1, 7), (2, 7), (3, 7), (4, 7), ..., (1, 9), (2, 9), (3, 9), (4, 9):

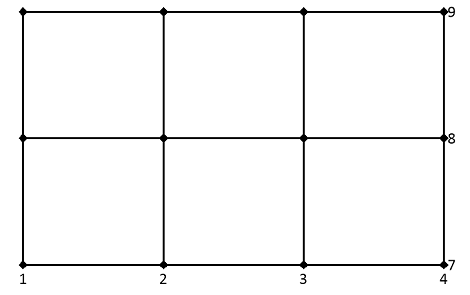
Les coordonnées des différents points de la grille sont obtenues par élément à partir des deux matrices portant les mêmes noms :

La fonction MeshGrid appliquée aux deux séries de données, aboutit maintenant à la liste constituée des matrices portant le même nom X (premier élément de la liste) et Z (deuxième élément de la liste).

Cette fonction est généralement utilisée pour représenter en trois dimensions des fonctions de y = f(x, z) de deux variables sur une grille rectangulaire bidimensionnelle. En particulier, cela permet d'utiliser des fonctions y = f(z) = f(z1, z2) avec des arguments de valeur complexe z = z1 + i * z2 peuvent être calculées et représentées sur le plan complexe.

Disponible dans

FlexPro Basic, Professional, Developer Suite

Exemples

Dim x = {1, 2, 3, 4}
Dim z = {7, 8, 9}
Dim grid = MeshGrid(x, z)
Dim y = grid.["X"]^2 - grid.["Z"] // = grid.[0]^2 - grid.[1]
Signal(y, x, z)
 

Exemple 1 : Procédure pour le calcul de fonctions avec deux variables

Calcule la fonction y = x^2 - z délimitant la grille à l'aide des séries de données {1, 2, 3, 4} (dans la direction X) et {7, 8, 9} (dans la direction Z) :

Dim x = Series(-4, 4, 0.01)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = ArcTan2(grid.["Z"], grid.["X"])
Signal(y, x, z)
 

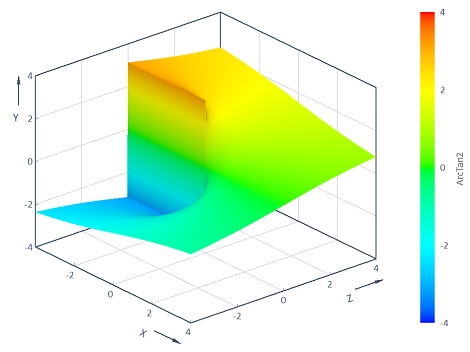
Exemple 2 : Visualisation de la fonction ArcTan2 avec 2 variables

Calcule la fonction ArcTan2 y = f(x, z) = ArcTan2(z, x) à travers la plage (x, z) bidimensionnelle [-4, 4] x [-4, 4]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Dim x = Series(-16, 16, 0.04)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = Sinc(Sqrt(grid.["X"]^2 + grid.["Z"]^2))
Signal(y, x, z)
 

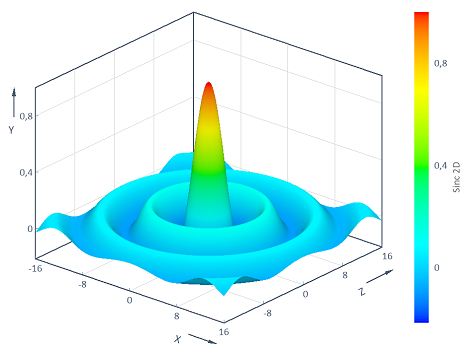
Exemple 3 : Visualisation de la fonction Sinc en 2D

Calcule la fonction Sinc bidimensionnelle y = f(x, z) = Sinc(Sqrt(x^2 + z^2)) à travers la plage (x, z) bidimensionnelle [-16, 16] x [-16, 16]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Dim z1 = Series(-6, 6, 0.02)
Dim z2 = z1
Dim grid = MeshGrid(z1, z2)
Dim y = Real(Log(grid.[0] + 1i * grid.[1]))
Signal(y, z1, z2)
 

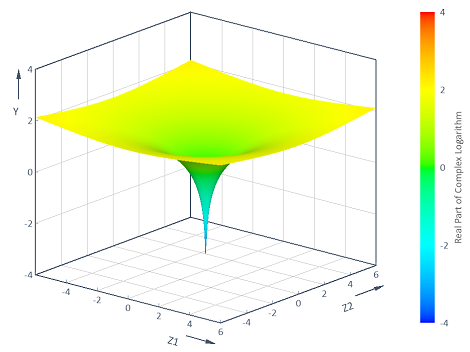
Exemple 4 : Visualisation de fonctions avec des arguments complexes

Calcule la partie réelle du logarithme complexe y = f(z1, z2) = Real(Log(z1 + i* z2)) à travers le plan (z1, z2) complexe [-6, 6] x [-6, 6]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Arguments x, z
Dim xMatrix = x # NumberOfRows(z)
Dim zMatrix = TransposeMatrix(z # NumberOfRows(x))
List("X", xMatrix, "Z", zMatrix)
 

Exemple 5 : Code FPScript équivalent

Le code FPScript suivant produit le même résultat que la fonction MeshGrid.

Voir aussi

Fonction ArcTan2

Fonction List

Fonction NumberOfColumns

Fonction NumberOfRows

Fonction Reshape

Fonction Shape

Fonction TransposeMatrix

Opérateur List

Opérateur List Element