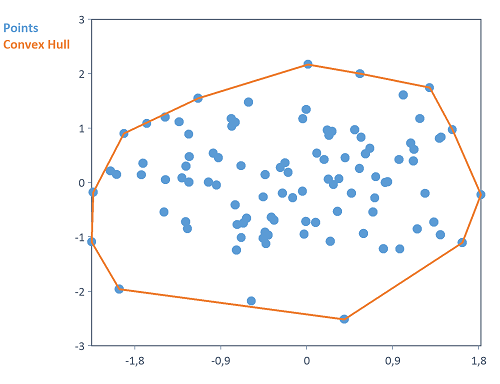
Calcule l'enveloppe convexe d'un ensemble de points bidimensionnel.
Syntaxe
ConvexHull(Points [ , le Algorithm Variable CONVEXHULL_GRAHAM_SCAN ])
ou
ConvexHull(Y, le X [ , le Algorithm Variable CONVEXHULL_GRAHAM_SCAN ])
La syntaxe de la fonction ConvexHull se compose des éléments suivants :
Section |
Description |
||||||
|---|---|---|---|---|---|---|---|
Points |
Les points Y et X pour lesquels l'enveloppe convexe doit être calculée. Les structures de données autorisées sont Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||
Y |
Les points Y utilisés pour calculer l'enveloppe convexe. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Série de données et Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
X |
Les points X utilisés pour calculer l'enveloppe convexe. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Série de données et Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
Algorithm |
Détermine l'algorithme de calcul de l'enveloppe convexe. L'argument Algorithm peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut CONVEXHULL_GRAHAM_SCAN . |
Remarques
Le résultat a toujours la structure de données Signal.
Les valeurs sont converties en valeurs à virgule flottante de 64 bits avant le calcul.
Disponible dans
FlexPro Basic, Professional, Developer Suite
Exemples
Dim y = Noise(1# 100, NOISE_NORMAL, 0)
Dim x = Noise(1# 100, NOISE_NORMAL, 0)
Dim points = Signal(y, x)
List("Points", points, "Convex Hull", ConvexHull(points))
Calcule l'enveloppe convexe de points répartis de façon aléatoire dans le plan bidimensionnel.