Calcule la transformée de Hilbert. Utilisé fréquemment pour calculer l'amplitude ou la fréquence instantanée ainsi que pour la démodulation des signaux.
Syntaxe
Hilbert(Signal [ , le FFTLength Variable 0 ])
La syntaxe de la fonction Hilbert se compose des éléments suivants :
Section |
Description |
|---|---|
Signal |
L'ensemble de données réelles à partir duquel le signal analytique doit être calculé. L'ensemble de données doit être échantillonné de manière équidistante, car l'algorithme utilise la transformée de Fourier discrète (pour les données équidistantes). Les structures de données autorisées sont Série de données, le Matrice de données, le Signal, le Série de signaux et Série de signaux avec composante X bidimensionnelle. Tous les types de données numériques sont autorisés, à l'exception de Temps calendaire et Période de temps. Les valeurs invalides ne sont pas autorisées dans cet argument. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
FFTLength |
La longueur de la transformée de Fourier nécessaire au calcul de la transformée de Hilbert. La longueur de la FFT doit être supérieure ou égale à la longueur des données. Si la longueur FFT indiquée est supérieure à la longueur des données, des zéros sont ajoutés pour la transformée de Fourier interne. Une valeur de -1 définit la longueur de la FFT à la puissance supérieure suivante de 2. La valeur par défaut 0 définit la longueur de la FFT à la longueur des données. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à -1. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 0 . |
Remarques
Le résultat a la même structure et la même unité que l'argument Signal.
Pour les structures de données composées, seule la composante Y est calculée. Les composantes X ou Z, si elles sont présentes, sont reprises telles quelles dans le résultat. Pour les matrices de données et les séries de signaux, le calcul s'effectue colonne par colonne.
La transformation de Hilbert est définie par une transformation intégrale linéaire pour un signal (à valeur réelle ou complexe) x(t) comme suit :
Par cette définition, sous la forme équivalente d'une convolution, la transformée de Hilbert peut également s'écrire comme :
En appliquant la transformée de Fourier à cette dernière équation, la fonction de transfert H de la transformée de Hilbert se calcule comme suit :
En d'autres termes, la transformation de Hilbert peut être interprétée comme un déphasage de -π/2 (c.-à-d. -90 degrés) pour les fréquences positives et de π/2 (c.-à-d. 90 degrés) pour les fréquences négatives. Par exemple, la transformation de Hilbert de la fonction cosinus donne comme résultat la fonction sinus.
Pour référence, voir [1] ainsi que [4].
Application : Amplitude instantanée, phase instantanée, fréquence instantanée, enveloppe et démodulation de signaux
La transformée de Hilbert est fréquemment utilisée pour calculer les grandeurs instantanées du signal original :Amplitude instantanée (Instantaneous Amplitude), le Phase instantanée (Instantaneous Phase) et Fréquence instantanée (Instantaneous Frequency). L'amplitude instantanée fournit également l'enveloppe supérieure du signal à analyser.
Grâce à ces grandeurs instantanées, les signaux peuvent également être démodulés (modulation d'amplitude, modulation de phase et modulation de fréquence).
Les calculs se réfèrent toutefois au signal analytique dérivé de la transformation de Hilbert et non pas directement à la transformation de Hilbert.
Les détails, définitions et exemples sont donc disponibles dans l'aide en ligne de la fonction AnalyticSignal ou de l'objet d'analyse Grandeur instantanée.
Contexte théorique : algorithme de calcul de la transformation de Hilbert
L'algorithme à temps continu susmentionné définit la fonction de transfert H dans la gamme de fréquences. L'algorithme de calcul de la transformation de Hilbert discrète est donc réalisé à l'aide de la FFT et de la fonction de transfert discrète H, de manière analogue à l'algorithme de la fonction AnalyticSignal (voir aussi [1]) :
La seule différence réside dans la définition de la fonction de transfert.
Celle-ci est maintenant donnée pour les longueurs FFT paires comme suit : H[k] = -i pour k = 1, 2, ..., FFTLength/2 - 1 (correspond aux fréquences positives) et H[k] = i pour k = FFTLength/2 + 1, ..., FFTLength (correspond aux fréquences négatives). i désigne ici l'unité imaginaire. Les coefficients symétriques k = 0 et k = FFTLength/2 sont spéciaux. Pour ceux-ci, H[k] = 0.
Pour les longueurs FFT impaires, la fonction de transfert est donnée par analogie comme suit : H[k] = -i pour k = 1, 2, ..., (FFTLength-1)/2 et H[k] = i pour k = (FFTLength-1)/2 + 1, ..., FFTLength ainsi que H[0] = 0.
L'algorithme FPScript pour le calcul de la transformation discrète de Hilbert correspond donc à l'algorithme FPScript de la fonction AnalyticSignal, à l'exception de la définition de la fonction de transfert. Un code similaire se trouve dans l'aide en ligne couvrant la fonction AnalyticSignal.
Influence de la longueur de la FFT : la résolution de la FFT nécessaire à l'algorithme est augmentée au moyen du "zero padding", c'est-à-dire en choisissant une longueur de FFT supérieure à la longueur des données. Le résultat du calcul peut ainsi être amélioré. L'exemple suivant permet de clarifier ce point.
Remarque Un signal à valeur réelle x(t) peut maintenant être transformé en un signal complexe z(t) au moyen de la transformation de Hilbert, comme suit :
La fonction de transfert de cette transformation correspond à la transformation de la définition de la fonction AnalyticSignal. La transformation de Hilbert peut donc être définie de manière équivalente comme la partie imaginaire du signal analytique associé au signal x(t).
Disponible dans
Option Analyse spectrale
Exemples
Imag(AnalyticSignal(realSig))
Il en résulte la transformation de Hilbert d'un signal de valeur réelle. Le code est équivalent à Hilbert(realSig).
realSig + 1i * Hilbert(realSig)
Transforme un signal à valeur réelle en un signal analytique dont la partie imaginaire correspond à la transformée de Hilbert. Le code est équivalent à AnalyticSignal(realSig).
Dim t = Series(0, 10, 0.005)
Hilbert(Signal(Cos(t), t))
Calcule la transformée de Hilbert de la fonction cosinus. Le résultat est la fonction sinusoïdale.
Dim t = Series(-25, 25, 0.005)
Dim sig = Signal(Sinc(t), t)
Dim hilbTrafo = Hilbert(sig, NumberOfRows(sig))
List("Hilbert Trafo calculated", hilbTrafo, "Hilbert Trafo exact", Signal((1-Cos(t))/t, t))
Calcule la transformée de Hilbert de la fonction Sinc. Le résultat exact, donné par la fonction 1/t - Cos(t)/t, est également affiché. La comparaison dans un graphique 2D fournit :
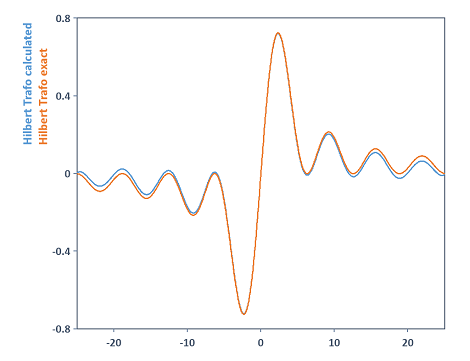
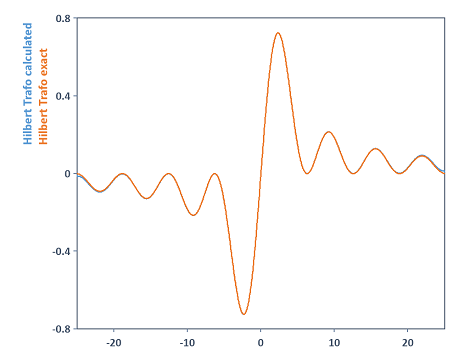
Dans cet exemple, si l'on augmente la longueur de la FFT lors du calcul de la variable hilbTrafo par exemple à la valeur 131072, cela fournit dans ce cas un résultat de calcul plus précis pour la transformation de Hilbert. Les deux courbes sont maintenant presque complètement en accord :
Voir aussi
Objet d'analyse Grandeur Instantanée
Littérature
[1] S. Lawrence Marple, Jr.: Computing the Discrete-Time "Analytic" Signal via FFT. Dans: IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222, le 1999.
[2] B. Boashash: Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals. Dans: Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono: On Instantaneous Amplitude and Phase of Signals. Dans: IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833, le 1997.
[4] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck: Discrete-Time Signal Processing, 2nd Ed.. Upper Saddle River, NJ: Prentice Hall, 1999.