weisang.com > Documents Articles > Objet et modèle d’analyse Ajustement de courbe non linéaire *

Documentation FlexPro

Objet et modèle d’analyse Ajustement de courbe non linéaire *

09.03.2021

L'objet d'analyse Ajustement de courbes non linéaires permet de faire converger une fonction modèle dépendant d'une variable indépendante et de plusieurs paramètres vers un ensemble de données donné. Un certain nombre de fonctions de modèle prédéfinies sont disponibles pour ce faire. Vous pouvez également définir des modèles particuliers.

Méthodes itératives et non itératives

Pour les méthodes d'ajustement de courbes non linéaires, vous pouvez distinguer les méthodes itératives et non itératives.

Les méthodes non itératives ne sont généralement pas considérées comme adaptées, car elles demandent beaucoup de temps. Cela justifie la méthode de la "recherche par grille". Dans ce cas, la plage à rechercher qui contient le minimum est divisée en une grille à n dimensions (n... nombre de paramètres de la fonction). Les résidus de la fonction sont calculés pour chaque point de grille. Le point où la somme des carrés résiduels est la plus faible donne le résultat. Si la grille est ensuite bissectée, le nombre d'appels de fonction augmente 2n fois. Avec la méthode "Recherche aléatoire", les points à calculer ne sont pas assignés comme des grilles, mais sont distribués aléatoirement. L'inconvénient de cette méthode est que, contrairement à la méthode itérative, la recherche des meilleurs paramètres n'est pas limitée par les calculs précédents. Un certain nombre d'appels de fonction coûteux et "inutiles" sont ainsi effectués.

Comme l'utilisation de la méthode itérative ne garantit pas que le résultat calculé soit un "minimum global", il est suggéré d'effectuer plusieurs calculs avec différents paramètres initiaux. Les algorithmes non itératifs sont utiles pour cela.

Dans FlexPro, la fonction FPScript ParameterEstimation est donc disponible pour fournir à la fois la méthode "Recherche par grille" et la méthode "Recherche aléatoire". En raison de la faible réponse à l'exécution déjà décrite, la fonction est principalement adaptée aux modèles simples avec peu de paramètres.

Parmi les méthodes itératives, on trouve les algorithmes proposés dans la fonction FPScript NonLinearCurveFit, qui convergent progressivement vers un minimum local.

Pour ce faire, les étapes suivantes sont réalisées :

•Les commutateurs de démarrage sont déterminés pour chaque paramètre du modèle de régression sélectionné (par exemple, en utilisant les méthodes non itératives).

•On calcule la courbe dans laquelle les valeurs des paramètres sont implémentées dans la fonction du modèle.

•La somme des carrés des distances verticales entre les points de données et la courbe est calculée.

•Les paramètres sont modifiés de manière à ce que la courbe converge mieux vers les points de données. Divers algorithmes sont utilisés à cet effet.

•Les étapes 1 à 4 sont répétées tant qu'un "bon" résultat est obtenu. Il existe plusieurs critères de convergence qui peuvent être définis à cet effet.

Une recherche est ainsi effectuée pour les paramètres d'un modèle, qui minimise autant que possible la somme des carrés résiduels pondérés et fournit ainsi une convergence appropriée à un ensemble de données donné.

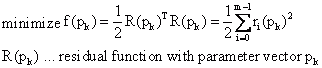
Des vecteurs avec des valeurs de paramètres sont calculés à partir d'un point de départ donné, qui convergent vers un minimum local. Les différentes méthodes se distinguent par le calcul de l'incrément, la direction de l'incrément et les critères de convergence.

Les algorithmes appliqués forment les méthodes suivantes :

Méthode Gauss-Newton

Pour la méthode Gauss-Newton, le modèle est linéarisé en utilisant l'expansion de Taylor. Le modèle linéarisé est ensuite utilisé pour minimiser la somme des carrés résiduels.

Méthode de la descente la plus abrupte

Lors de la recherche du minimum, la direction de la descente est spécifiée par les gradients (négatifs) de la fonction.

Ainsi, la méthode est également appelée méthode du gradient. En règle générale, il trouve l'optimum assez lentement, ce qui signifie qu'il converge mal.

Méthode Levenberg-Marquardt

La méthode de Levenberg-Marquardt combine la méthode de Gauss-Newton avec la méthode descente la plus abrupte. Le rayon de la "région de confiance" utilisé pour la méthode influence l'incrément et la direction de l'incrément. Elle fournit une limite supérieure pour la norme euclidienne de la direction de recherche et influence ainsi la méthode utilisée (Gauss-Newton ou descente la plus abrupte).

Méthode de Newton

Contrairement à la méthode Gauss-Newton, cette méthode examine la partie carrée de l'expansion de Taylor. Ainsi, la matrice hessienne (dérivées partielles secondes) est nécessaire pour le calcul. Comme la matrice hessienne peut rarement être spécifiée analytiquement, elle doit être approximée. Cela se produit, par exemple, via la méthode sécante. Les bons algorithmes remplacent la matrice hessienne afin d'utiliser les informations déjà disponibles et d'obtenir ainsi une meilleure approximation. Au lieu de H(x), seul S(x) est approximé :

Matrice hessienne :

Calcul de l'itération suivante p+ à partir d'un point pk :

Méthodes	Calculé en utilisant
Gauss-Newton
Levenberg-Marquardt
Newton
NL2SOL

Algorithmes

Pour les algorithmes utilisés dans l'ajustement de courbes non linéaires, une procédure de Moré dans un paquet MINPACK (algorithme de Levenberg Marquardt) et une variante de l'algorithme NL2SOL (algorithme de Full Newton). Dans la section Références, on peut trouver deux algorithmes qui ont presque la même valeur. Il n'y a pas de grande différence pour les problèmes avec de petits résidus. L'algorithme NL2SOL, plus complexe, est toutefois préféré pour les problèmes présentant des résidus plus importants ou pour les problèmes extrêmement non linéaires, car il nécessite moins d'itérations. En outre, les limites des paramètres à trouver sont conservées lors de la mise en œuvre des variations de l'algorithme NL2SOL et la plage à rechercher est donc limitée. Les deux algorithmes ont déjà été testés de manière approfondie pour leur applicabilité et leur robustesse.

Pour les deux algorithmes, les dérivées partielles nécessaires au calcul peuvent être calculées analytiquement ainsi que "par approximation par différence directe". Lorsqu'elles sont calculées analytiquement, les dérivées partielles sont spécifiées sous forme de formules. C'est le cas pour presque tous les modèles donnés. Si les dérivés ne sont pas spécifiés pour un modèle personnalisé, ils sont approximés.

Un algorithme de Levenberg-Marquardt modifié est utilisé pour l'algorithme LMDER ou LMDIF dans MINPACK. Moré utilise une méthode de "région de confiance" à échelle réduite.

L'algorithme NL2SOL est basé sur la méthode des "moindres carrés" de Newton. Il contient une méthode sécante pour calculer la matrice hessienne. En outre, une stratégie de "région de confiance" est utilisée. Pour les problèmes avec de petits résidus, l'algorithme est simplifié en une méthode de Levenberg-Marquardt ou de Gauss-Newton. Les deux algorithmes sont disponibles sur Internet à l'adresse www.netlib.org.

Modèle

FlexPro offre une variété de fonctions modèles prédéfinies auxquelles les données à analyser peuvent être adaptées. Après avoir sélectionné un modèle, vous pouvez visualiser la formule et une esquisse du modèle associé dans un volet d'aperçu. Vous pouvez accéder directement à l'aide en ligne de FlexPro pour les fonctions des modèles en utilisant le bouton Aide sur les modèles. La fonction actuelle du modèle peut être visualisée, par exemple, pendant que vous définissez les valeurs initiales des paramètres, ce qui vous évite de devoir passer d'un onglet à l'autre.

Modèles Pics

Un certain nombre de modèles pics prédéfinis sont disponibles et peuvent être modifiés en utilisant le nombre de pics et les informations pour une fonction de base. Pour les modèles comportant plusieurs pics, certains paramètres du modèle peuvent être utilisés ensemble. Ceci peut être configuré dans la liste des paramètres . À partir de ces informations, un modèle de pic "spécial" est généré dynamiquement et utilisé pour l'ajustement de la courbe non linéaire. FlexPro propose l'ajustement des pics dans l'assistant d'analyse en tant que modèle d'analyse séparé.

Modèle Personnalisé

Si le modèle à analyser ne se trouve pas dans la liste des fonctions de modèle prédéfinies, un modèle personnalisé peut être défini et enregistré dans le profil de l'utilisateur. Pour ce faire, vous devez d'abord sélectionner le modèle (modèle personnalisé). La zone de texte Fonction apparaît où le modèle personnalisé est saisi. Les paramètres d'un modèle personnalisé dont le nombre de paramètres est de n sont nommés p[0], p[1], ..., p[n-1]. La variable indépendante est x.

Exemple de fonction sinus : p[0] * sin(2 * PI * p[1] * x + p[2])

Vous pouvez également attribuer des noms aux paramètres. Ces noms apparaissent ensuite dans la liste des Valeurs initiales. Pour ce faire, vous devez attribuer des noms aux variables de paramètres p[0] ... p[n-1] dans la formule qui décrit la fonction du modèle personnalisé.

Dim Amplitude = p[0]
Dim Fréquence = p[1]
Dim Phase = p[2]

La variable Amplitude est affectée à la variable p[0], la Fréquence est affectée à la variable p[1], et la Phase est affectée à la variable p[2]. Vous devez veiller à ce que les affectations soient effectuées les unes en dessous des autres. Dans la fonction modèle, vous pouvez maintenant remplacer les variables p[0] à p[n-1] :

Amplitude * sin(2 * PI * Fréquence * x + Phase)

Lorsque vous définissez un modèle personnalisé, il est important d'entrer le nombre correct de paramètres. Si cette valeur est incorrecte, l'ajustement de courbe non linéaire ne peut pas être calculé ou renvoie un résultat incorrect.

•Calculer les dérivées partielles de manière analytique

Les algorithmes d'ajustement de courbes non linéaires nécessitent les dérivées partielles des paramètres du modèle pour le calcul. Les dérivées peuvent être calculées analytiquement ainsi que par "approximation de différence directe". Lorsqu'elles sont calculées analytiquement, les dérivées partielles sont spécifiées sous forme de formules. La formule qui décrit les dérivées doit être spécifiée comme une liste avec n (nombre de paramètres) fonctions dérivées.

Exemple :

Dim Amplitude = p[0]

Dim Fréquence = p[1]

Dim Phase = p[2]

[ sin(2 * PI * Fréquence * x + Phase), 2 * PI * x * Amplitude * cos(2 * PI * Fréquence * x + Phase), Amplitude * cos(2 * PI * Fréquence * x + Phase) ]

•Enregistrer le modèle

Vous pouvez enregistrer un modèle personnalisé dans votre profil d'utilisateur. Pour ce faire, vous devez saisir un nom dans la zone de liste Modèle et appuyer sur Enregistrer le modèle. Tous les modèles enregistrés apparaissent dans la zone de liste Modèle. Si vous sélectionnez un modèle personnalisé, vous pouvez le supprimer du profil utilisateur en appuyant sur le bouton Supprimer le modèle.

•Modèle personnalisé à partir d'une formule

Vous pouvez également enregistrer des modèles personnalisés dépendant de la base de données en configurant des formules avec les fonctions de modèle. Pour ce faire, vous devez sélectionner le modèle (Modèle personnalisé à partir de la formule) et spécifier la formule du modèle généré comme fonction. La syntaxe des formules du modèle est décrite dans la section Modèle personnalisé. Toutefois, le contenu de la formule doit être placé entre guillemets, car les formules du modèle doivent être du type chaîne de caractères.

La formule pour le modèle ci-dessus devrait ressembler à ce qui suit :

"Dim Amplitude = p[0]\r\n_
Dim Fréquence = p[1]\r\n_
Dim Phase = p[2]\r\n_
Amplitude * sin(2 * PI * Fréquence * x + Phase) "

La formule des dérivées partielles doit contenir le code suivant :

"Dim Amplitude = p[0]\r\n_
Dim Fréquence = p[1]\r\n_
Dim Phase = p[2]\r\n_
[ sin(2 * PI * Fréquence * x + Phase),_
2 * PI * x * Amplitude * cos(2 * PI * Fréquence * x + Phase),_
Amplitude * cos(2 * PI * Fréquence * x + Phase) ]"

Les caractères "\r\n" génèrent un saut de ligne dans une chaîne et doivent être utilisés si votre code contient plusieurs instructions. Dans cet exemple, le caractère "_" a été utilisé à la fin des lignes pour que la chaîne de caractères puisse être répartie sur plusieurs lignes.

Évaluation des modèles (uniquement dans l'assistant d'analyse)

Avec cet outil, vous pouvez comparer le calcul de plusieurs fonctions modèles entre elles. Le classement des modèles sélectionnés se fait par la somme des carrés résiduels absolus SSE. Pour plus d'informations à ce sujet, reportez-vous au didacticiel sur l'ajustement de courbes non linéaires.

Paramètres

Le choix des valeurs initiales des paramètres du modèle est déterminant pour le calcul du résultat. Si le point de départ sélectionné est très éloigné du minimum global, l'algorithme peut ne pas renvoyer de résultat ou renvoyer un minimum local différent. Pour l'algorithme de Newton complet, une limite de portée(limites supérieure et inférieure) est spécifiée pour chaque paramètre, ce qui réduit la portée de la recherche.

Certains paramètres du modèle sélectionné peuvent être déclarés comme fixes. Pour l'algorithme de Newton complet, les limites supérieure et inférieure sont fixées à la valeur initiale spécifiée. Pour l'algorithme de Levenberg-Marquardt, la variable paramètre dans la fonction modèle est remplacée par la valeur initiale constante.

Estimer les valeurs initiales (uniquement dans l'assistant d'analyse)

Pour augmenter la probabilité qu'un minimum global figure dans le résultat affiché, le calcul doit être effectué avec différentes valeurs initiales. Pour les modèles comportant quatre paramètres ou moins, l'option Estimer les paramètres initiaux. Pour chaque paramètre, on calcule 10 valeurs distribuées aléatoirement qui se trouvent dans l'intervalle déterminé par les limites supérieure et inférieure. Pour chaque combinaison, la somme absolue des carrés résiduels est maintenant calculée. La combinaison avec la somme moyenne des moindres carrés fournit les valeurs initiales.

Démarrer le script

Les valeurs initiales des paramètres peuvent également être calculées à l'aide d'une formule FPScript. Lorsque vous faites cela, assurez-vous que le résultat de la formule renvoie une série de données avec n (nombre de paramètres du modèle) valeurs. Sinon, le script de démarrage est ignoré. Pour modifier la formule, cliquez sur le bouton Démarrer le script. Vous pouvez modifier le code dans la boîte de dialogue qui apparaît. Utilisez la variable data pour accéder aux données. Vous pouvez utiliser le bouton Calculer. En cliquant sur Appliquer, vous acceptez les paramètres calculés. En outre, dans l'assistant d'analyse, vous pouvez sélectionner l'option Utiliser le script de démarrage. Le script de départ est alors automatiquement calculé à chaque fois que le modèle est modifié ou lorsque l'ajustement de la courbe non linéaire est à nouveau appelé.

Pondération

La détermination du meilleur paramètre en utilisant la minimisation de la somme des carrés résiduels repose sur l'hypothèse que la dispersion des valeurs est égale à la courbe déterminée d'une distribution gaussienne. La méthode de l'erreur quadratique moyenne est une estimation de la vraisemblance maximale si les erreurs de mesure sont indépendantes et normalement distribuées (distribution gaussienne) et ont un écart type constant. Les valeurs mesurées qui sont plus éloignées de la courbe donnée influencent la somme des carrés résiduels plus fortement que les points plus proches.

Si la diffusion est la même pour tous les points de données, aucune pondération n'est nécessaire. Le vecteur de pondération W est égal à 1 pour chaque paramètre.

Il existe également des situations expérimentales dans lesquelles la distance des résidus augmente lorsque Y augmente. Si l'espacement absolu des points de la courbe augmente avec Y, mais que l'espacement relatif (espacement divisé par Y) reste constant, une pondération relative de W = 1/Y2 est logique. Ainsi, la somme des carrés des distances est :

La pondération de Poisson de W = 1/Y représente un compromis entre la minimisation de la distance relative et absolue. Pour une distribution de Poisson, les points suivants sont particulièrement importants :

En outre, la somme des carrés résiduels peut être pondérée par la variance. Si les données à examiner sont spécifiées comme une matrice de données ou une série de données, la variance s2 avec le réglage"Pondération avec 1/s2, 1/s2 est déterminé à partir de la matrice de données" sur les données et est utilisé comme pondération :

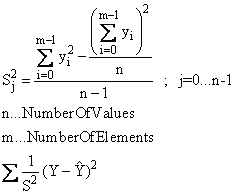
La variance s2 est ensuite spécifiée via un ensemble de données. La longueur de données de la variance doit être égale à la longueur de données de l'ensemble de données à examiner.

Mise à l'échelle

Un des problèmes de l'ajustement non linéaire des courbes peut être la mauvaise mise à l'échelle des paramètres individuels du modèle. Par exemple, une variable peut se déplacer dans une plage de [102, 103] mètres et une autre dans un intervalle de [10-7, 10-6] secondes. Si ce point est ignoré, cela peut avoir une influence négative sur les résultats calculés.

Par conséquent, pour les algorithmes respectifs, différentes options de mise à l'échelle(pas de mise à l'échelle, mise à l'échelle adaptative, mise à l'échelle à partir de la matrice jacobienne initiale, mise à l'échelle à partir des limites, mise à l'échelle personnalisée) sont disponibles. Dans l'exemple fourni, vous pourriez sélectionner une échelle personnalisée et recalculer le premier paramètre en kilomètres et le second en millisecondes. Les deux paramètres se situent alors dans l'intervalle [10-1,1]. En plus d'influencer l'algorithme, la mise à l'échelle joue un rôle important dans le calcul de divers critères de convergence. Lors du calcul sans mise à l'échelle, les paramètres ayant une très petite plage de valeurs sont ignorés lors du test des critères de convergence.

Critères et paramètres de résiliation

Il est important de savoir, lors du calcul des paramètres, comment vous devez terminer l'algorithme. La question est de savoir quand un calcul peut être achevé avec succès et quand il est temps d'interrompre le calcul avec un message d'erreur.

Il existe une variété de critères de convergence qui déterminent si les paramètres actuellement calculés sont suffisamment proches de la solution souhaitée pour que le calcul puisse être achevé. Les tolérances de convergence peuvent être définies via les paramètres Tolérance X, Tolérance Y, Tolérance F ou Tolérance G. Le calcul des critères de convergence est différencié par les algorithmes.

•L'algorithme NL2SOL comprend 5 tests de convergence :

- Convergence X (critère de convergence des paramètres relatifs)

- convergence relative des fonctions

- convergence absolue des fonctions

- convergence singulière

- fausse convergence

Les trois premiers critères de convergence peuvent être influencés par les options de paramétrage Tolérance X, Tolérance Y et Tolérance F. La convergence de la fonction absolue se produit lorsqu'une itération pk est trouvée où elle s'applique pour une tolérance F-Tolerance donnée.

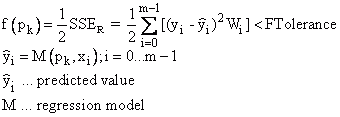
Les autres critères de convergence ne sont alors exécutés que si l'étape courante Δpk ne conduit pas à plus du double de la réduction de la fonction prédite :

Les tests de convergence sont fortement influencés par le modèle carré actuel qk, qui est assez peu fiable, si l'inégalité spécifiée n'est pas remplie. Ce test offre donc une protection supplémentaire quant à la fiabilité des autres critères de convergence.

X Convergence (XTolerance) teste les changements relatifs des paramètres mis à l'échelle par étape d'itération :

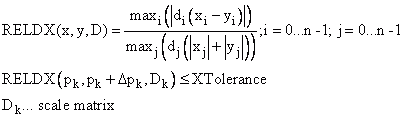
La convergence relative de la fonction (YTolerance) est obtenue lorsque la fonction avec les paramètres calculés actuels est proche d'une fonction estimée f(p*) avec un fort minimiseur local p*. La fonction estimée converge via un modèle carré :

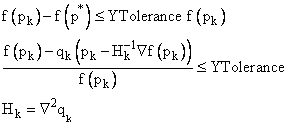
•Minpack:

La convergence relative des paramètres (convergence X) est basée sur la relation entre la variation absolue du paramètre et la variation relative de la norme euclidienne du paramètre. Ce critère de convergence peut être influencé par le paramètre Tolérance X.

Pour tester la convergence de la fonction relative, l'algorithme MINPACK LMDER ou LMDIF calcule la variation relative actuelle de la somme des carrés pendant une itération et la variation relative estimée sur la base d'un modèle linéaire. Le critère de convergence est rempli lorsque les deux changements relatifs sont inférieurs à la tolérance Y donnée.

Le paramètre G-Tolerance permet de déterminer la valeur du cosinus de l'angle entre les colonnes de la matrice jacobienne actuelle et le vecteur résiduel correspondant. L'orthogonalité peut donc être déterminée. Une relation mathématique entre ce test et le test de convergence relative des paramètres dans l'algorithme NL2SOL peut être produite (comparer à Dennis : Un algorithme adaptatif non linéaire des moindres carrés).

En outre, vous pouvez spécifier le nombre maximum de fois que la fonction peut être appelée pour calculer les résidus avant que le calcul ne soit interrompu. Il est possible que la fonction résiduelle soit appelée plusieurs fois par étape d'itération. Vous ne devez donc pas spécifier le nombre maximum d'itérations, mais plutôt le nombre minimum d'appels de fonction.

La longueur initiale du pas peut être modifiée à l'aide de la fonction Pas à pas principal. Cette valeur doit être modifiée dans les situations où l'on veut éviter que la première étape soit trop grande, ce qui, par exemple, conduit à un dépassement exponentiel. Le diamètre de la "région de confiance" est déterminé, dans laquelle les meilleurs paramètres peuvent être recherchés pendant la première itération.

Résultat / Sortie (uniquement dans l'objet d'analyse)

L'état de sortie décrit la raison pour laquelle un calcul a été interrompu. Une distinction est faite entre deux groupes. L'algorithme se termine avec succès si certains critères de convergence sont remplis. Si ce n'est pas le cas, l'algorithme interrompt le calcul sur la base des critères de résiliation. Toutefois, les critères de convergence ne suffisent pas à eux seuls à déterminer le résultat de l'ajustement non linéaire de la courbe. Différentes options de résultat statistique sont donc disponibles, permettant de déterminer la qualité de l'ajustement.

L'ajustement non linéaire de la courbe vous offre deux possibilités de résultat. Vous pouvez calculer les paramètres une fois et les entrer de manière statique dans la fonction de modèle sélectionnée. Pour cela, utilisez la fonction NonLinModel pour les modèles prédéfinis. Pour générer un modèle statique, vous devez appuyer sur le bouton Calculer Curve Fit. Les valeurs calculées apparaissent dans la liste des paramètres. Vous pouvez également déterminer dans l'onglet Résultats quelles grandeurs caractéristiques statistiques doivent être renvoyés. Si plusieurs options de résultat sont sélectionnées, l'objet d'analyse renvoie une liste comme résultat. (Voir NonLinearCurveFit)

Références

•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3e édition, McGraw-Hill, New York, 2003.

•W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery. Numerical Recipes in C. 2nd ed. Cambridge, U.K., Cambridge Univ. Press, 1992.

•G. A. F. Seber, C. J. Wild. Nonlinear Regression. Wiley, New York, 2003.

•K. Madsen, H.B. Nielsen, O. Tingleff, Methods for non-linear least squares problems, 2nd Edition, IMM, DTU, April 2004

•P.E. Frandsen, K. Jonasson, H. B.Nielsen. Unconstrained Optimization, 3nd Edition, IMM, DTU, March 2004

•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.

Vous pouvez trouver des informations sur les algorithmes ici :

•J. E. Dennis Jr., Robert B. Schnabel. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Classics in Applied Mathematics 16, SIAM Society for Industrial and Applied Mathematics, 1996.

•J. E. Dennis, Jr., D. M. Gay, and R. E. Welsch. An Adaptive Nonlinear Least Square Algorithm, ACM Trans. Math. Software 7, 1981, pp. 348-368 and 369-383

•J. E. Dennis, Jr., D. M. Gay, and R. E. Welsch. Algorithm 573. NL2SOL -- An adaptive nonlinear least-squares algorithm, ACM Trans. Math. Software 7, 1981, pp. 369-383.

•D.W. Marquardt. An Algorithm for Least-Squares Estimation of Nonlinear Parameters, Journal of the Society for Industrial and Applied Mathematics, vol. 11, 1963, pp 431-441.

•Jorge J. Moré. The Levenberg-Marquardt Algorithm: Implementation and Theory, Numerical Analysis, Lecture Notes in Mathematics, vol. 630, G.A. Watson, ed. (Berlin: Springer Verlag), 1977, pp. 105- 116.

•J. J. Moré, B. S. Garbow, and K. E. Hillstrom. User Guide for MINPACK-1, Argonne National Laboratory Report ANL-80-74, Argonne, Ill., 1980. Internet: http://www.netlib.org/minpack/ex/file06

•P. A. Fox, A. D. Hall, and N. L. Schryer. The PORT mathematical subroutine library, ACM Trans. Math. Software 4, 1978, pp. 104-126.

•D. M. Gay. Usage summary for selected optimization routines, Computing Science Technical Report No. 153, AT\&T Bell Laboratories, Murray Hill, NJ, 1990.

•K.L. Hierbert. An Evaluation of Mathematical Software that Solves Nonlinear Least Squares Problems. ACM Trans. Math. Software, Vol. 7, No. 1, 1981, pp. 1-16.