Analyse spectrale de Fourier
Décomposition de Fourier
La transformée de Fourier rapide (FFT) décompose un signal dans le domaine temporel (qui peut être une fonction du temps, des coordonnées spatiales ou de toute abscisse de série temporelle) en exponentielles complexes (sinus et cosinus). Une transformée de Fourier offre une image complète de l'espace des fréquences, mais ne retient aucune information quant au moment où un signal se produit dans le temps. Ainsi, un signal doit soit être stationnaire au sens large, avec une moyenne et une variance constantes sur de larges segments temporels, soit se préoccuper uniquement de manière qualitative de savoir si un certain signal de fréquence se produit quelque part dans la plage temporelle échantillonnée.
La FFT est une voie algorithmique rapide pour produire la transformée de Fourier discrète (DFT). Les transformées discrètes avant et arrière sont définies comme suit :
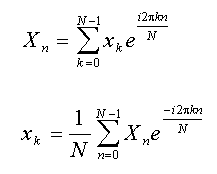
Bien que la DFT soit très simple, il s'agit d'une procédure d'ordre n². D'autre part, la FFT est un n*log2(n). La différence de temps de traitement est spectaculaire avec les grands ensembles de données. La FFT meilleur exact-n de FlexPro utilise quatre algorithmes FFT différents.
Les décompositions de Fourier sont limitées en résolution, car les fréquences auxquelles les sinus et les cosinus sont calculés sont espacées de manière égale et en nombre fixe. Pour un ensemble de données de n points, il y aura n fréquences complexes. Pour les données réelles, les fréquences négatives reflètent les fréquences positives, et seules les fréquences positives sont affichées. Ainsi, n / 2+1 fréquences composent le spectre. Les fréquences normalisées vont de 0, parfois appelé DC, à 0,5, la fréquence de Nyquist. La fréquence 0 est le décalage ou la valeur moyenne du signal temporel et est souvent décrite comme DC. La fréquence de Nyquist est la fréquence maximale qui peut encore être détectée compte tenu de la fréquence d'échantillonnage choisie. Il y a encore deux valeurs d'échantillonnage par période dans le signal temporel pour les composantes du signal de cette fréquence. FlexPro affiche les fréquences réelles. Les fréquences normalisées ne sont utilisées que si l'information temporelle n'est pas présente dans l'ensemble de données.
Fonctions de base continues
La décomposition de Fourier représente une séquence de données comme une combinaison linéaire d'un ensemble de sinus et de cosinusoïdes. Bien que les données et les séquences de Fourier soient chacune discrètes, les fonctions de base sont continues et d'une durée infinie. Il est donc possible de reconstruire le signal pour n'importe quel moment dans l'intervalle de la séquence originale :
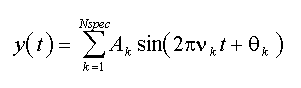
Les fonctions de base de Fourier peuvent être traitées comme des exponentielles complexes, des paires de sinus et de cosinus de phase nulle, des cosinus porteurs de phase ou des sinus porteurs de phase. Dans FlexPro, les fonctions de base de Fourier sont rapportées comme des fonctions élémentaires de cosinus portant la phase dans une gamme allant de -π/2 to +π. Dans l'équation ci-dessus, A est l'amplitude rapportée, ν est la fréquence, et θ est la phase. Le signal à tout instant t peut être reconstruit en additionnant la valeur de tous les Nspec cosinusoïdes dans le spectre évalué à cet instant. Les amplitudes sont ajustées de manière à ce que toute la puissance soit représentée dans les fréquences positives.
Fuite spectrale
La fuite spectrale est le terme utilisé pour décrire la perte de puissance d'une fréquence donnée vers d'autres cases de fréquence dans la FFT. L'approximation d'un flux de données fini par une série de Fourier infinie suppose que les données sont entièrement périodiques. Peu d'ensembles de données mettent effectivement en évidence cette propriété d'enveloppement continu. Au lieu de cela, il y a des effets de bord provenant de la discontinuité aux limites qui provoquent une fuite spectrale. La fuite spectrale se produit également en raison des fréquences fixes linéaires utilisées dans la FFT.
À moins que la fréquence d'une sinusoïde ne corresponde exactement au centre d'une case de fréquence de la FFT, une partie du signal s'échappera vers d'autres cases. On peut donc s'attendre à ce qu'une partie des bacs adjacents reflète également une certaine mesure de ce pic. En effet, lorsque la fréquence d'une composante spectrale n'est pas centrée dans une case, une partie de la variance due à cette composante peut être prise en compte par chaque case du spectre. Ce phénomène tend à diminuer au fur et à mesure que l'on s'éloigne de la fréquence qui nous intéresse, même s'il y aura des harmoniques. Un sinus et un cosinus à des multiples de la fréquence originale, par exemple, devraient également capturer une partie de la variance.
D'un autre point de vue, une FFT peut être considérée comme un ajustement linéaire des moindres carrés aux fonctions sinus et cosinus à des fréquences fixes linéairement croissantes. Si une seule onde sinusoïdale est ajustée de manière non linéaire, les paramètres peuvent être entièrement résolus puisque l'amplitude, la fréquence et la phase peuvent chacune varier afin de trouver l'optimum. Ceci n'est pas possible dans une FFT. Si l'amplitude et la phase peuvent varier, les fréquences, elles, ne le peuvent pas. À moins que la fréquence de l'onde sinusoïdale ne tombe exactement sur l'une des fréquences fixes de la FFT, la composante sinusoïdale sera étalée sur plusieurs fréquences.
Si la fuite spectrale attribuable aux fréquences fixes est une partie intrinsèque d'un spectre de Fourier, on peut faire beaucoup pour éliminer les effets de bord. Pour produire une fuite spectrale minimale, les données peuvent se rapprocher d'une séquence infinie en diminuant jusqu'à zéro aux deux extrémités. Pour ce faire, on utilise une fenêtre d'observation de données.
Fenêtre d'observation des données
Ces fenêtres sont généralement appliquées dans le domaine temporel, même si elles sont construites dans le domaine fréquentiel. Cela s'explique par le fait qu'une simple multiplication suffit à mettre en œuvre la pondération dans le domaine temporel. FlexPro offre une large gamme de fenêtres d'observation ayant du mérite dans le traitement du signal.
Une fenêtre rectangulaire (aucune fenêtre réelle n'est appliquée) produit une largeur de bande unilatérale de 1,0 dans le domaine des fréquences. Les fenêtres d'observation de données dans FlexPro varient en largeur de bin de Fourier de 1,1 à 6,0. De nombreuses fenêtres populaires ont des largeurs de 2,0, 3,0 et 4,0. Lorsqu'un ensemble de données est fenêtré, les parties du signal les plus proches des limites sont écartées et la résolution est dégradée. Une fenêtre avec une largeur de bin de 2,0 n'aura que la moitié de la résolution de son homologue non fenêtré. Une fenêtre avec une largeur de bac de 4,0 n'aura qu'un quart de la résolution.
Bien qu'une partie de l'influence des données soit écartée ou diminuée, et malgré la perte de résolution, les FFT fenêtrées sont souvent la meilleure solution pour une estimation précise des composantes spectrales, surtout lorsqu'une gamme dynamique élevée est nécessaire. En faisant varier les données de façon régulière et en les ramenant à zéro aux extrémités, la fuite spectrale est considérablement réduite, à tel point qu'une échelle en décibels (dB), qui est logarithmique, doit être utilisée pour observer la fuite spectrale à travers les bins de façon significative.
Lorsqu'une FFT traite des données qui ont été pondérée par une fenêtre temporelle, chaque bin de fréquence devient effectivement plus large. Cette largeur est parfois appelée l'ordre de la fenêtre. Les fenêtres de Hann et de Hamming répartissent le signal sur 2 bins et sont donc des fenêtres d'ordre 2. Cet étalement élimine une grande partie des fuites spectrales associées au fait de se trouver trop près du bord d'une case de fréquence. Bien qu'il existe une variété de propriétés de fenêtres d'observation, la largeur de bin est certainement la plus importante car elle détermine la résolution du signal ainsi que la gamme dynamique que la FFT est capable de représenter. Chaque fenêtre a une forme caractéristique qui fixe la plupart des propriétés de résolution du spectre de fréquence résultant. Certaines fenêtres ont un paramètre ajustable, et pour toutes les fenêtres d'observation de données de FlexPro, ceci contrôle la largeur du pic dans le domaine fréquentiel.
La commande de la plupart des fenêtres réglables a été modifiée pour refléter directement cette largeur de bac. Certaines fenêtres minimisent les fuites au niveau des lobes latéraux adjacents, au prix d'une décroissance de fréquence faible à négligeable (rolloff) à mesure que l'on s'éloigne du pic de fréquence. Ces fenêtres donnent une excellente résolution des pics de puissance variable très rapprochés dans le spectre, mais peuvent masquer les pics de faible puissance éloignés des fréquences de pointe. La fenêtre de Tchebychev produit le pic le plus étroit possible pour un niveau de fuite spécifique du lobe latéral (harmonique adjacent). D'autres fenêtres maximisent la décroissance ou l'atténuation des fuites spectrales, mais ne sont pas aussi efficaces pour minimiser les fuites aux fréquences proches. Deux pics distants en fréquence, chacun de faible puissance, peuvent être bien détectés, mais dans le cas de deux pics rapprochés, l'un de plus grande puissance peut masquer entièrement l'autre de moindre puissance.
Il y a donc deux critères de conception essentiels dans le choix d'une fenêtre d'observation des données. La première est la résolution. Sélectionnez la plus grande largeur de bac qui offre une résolution acceptable. La seconde consiste à sélectionner une fenêtre de cet ordre en fonction du fait que vous souhaitez ou non résoudre principalement des pics éloignés de faible puissance (lorsqu'une fenêtre de rolloff maximum est sélectionnée), ou qu'un pic de faible puissance peut se trouver dans l'ombre d'une composante proche de plus grande puissance. Souvent, un compromis est choisi. Les fenêtres les plus connues, telles que la populaire fenêtre de Blackman-Harris à 4 paramètres ( Cos4 Blackman-Harris ), sont généralement celles qui minimisent la fuite spectrale des lobes latéraux adjacents.
La fenêtre Flattop représente une caractéristique unique. Cette fenêtre a une largeur maximale du lobe principal de 5, offrant ainsi une résolution spectrale relativement faible ; cependant, le maximum du lobe principal a presque la même valeur dans la bande complète d'une ligne de fréquence à sa voisine à gauche et à droite. Le maximum du lobe principal présente donc un pic large, mais plat. Cette fenêtre est particulièrement adaptée à la mesure des puissances ou des amplitudes des composantes de signaux à bande étroite, c'est-à-dire des pics individuels dans un spectre. Grâce au type particulier de maximum du lobe principal, la hauteur d'un pic est en fait indépendante de son emplacement entre deux lignes de fréquence.
Moyenne des périodogrammes
Les fenêtres de données éliminent les informations proches des limites de la fenêtre d'observation, en mettant l'accent sur les propriétés spectrales des données proches du centre de l'enregistrement. Si les données sont vraiment stationnaires au sens large, le seul problème est la variabilité supplémentaire résultant de l'utilisation d'une partie seulement des données. Le périodogramme est une option spectrale qui répond à cette préoccupation. Dans cette procédure, on fait la moyenne d'une série de TFR fenêtrées à plus petits segments qui se chevauchent, ce qui réduit la variance au prix d'une diminution de la résolution spectrale.
Analyse Multitaper
Un autre algorithme qui traite de l'utilisation des informations proches des limites de l'enregistrement des données est le Spectre Multitaper. Dans cette procédure, on fait la moyenne des spectres d'un ensemble de fenêtres d'observation orthogonales. Le spectre résultant d'une analyse multitaper a également une variance réduite, toutes les données sont représentées et la résolution spectrale est comparable à celle d'une FFT fenêtrée de taille normale.
Références
Une bonne introduction au traitement du signal numérique est :
•Oppenheim, A. V. and Schafer, R. W. (1989). Traitement des signaux en temps discret. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). Transmission du signal. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Les algorithmes FFT utilisés dans FlexPro sont décrits dans :
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, June 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, p.1249, May-June 1969
Des informations sur les fenêtres d'observation de données sont fournies dans :
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981. 1981.
Des informations sur les spectres multitaper peuvent être trouvées dans :
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.
