Filtre l'ensemble de données avec un filtre de lissage Savitzky-Golay (également appelé Lissage des moindres carrés).
Syntaxe
SavitzkyGolayFilter(DataSet, le SmoothingWidth, le [ PolynomialOrder Variable 2 ] [ , le Extrapolate Variable TRUE ])
La syntaxe de la fonction SavitzkyGolayFilter se compose des éléments suivants :
Section |
Description |
|---|---|
DataSet |
L'ensemble de données à filtrer (lisser). Toutes les structures de données sont autorisées, sauf Scalaire et Liste. Tous les types de données numériques sont autorisés. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
SmoothingWidth |
Spécifie combien de valeurs voisines, y compris la valeur à lisser, doivent être incluses dans le lissage. La largeur de lissage doit être un nombre impair. Sinon, l'intervalle est asymétrique, et une valeur supplémentaire est incluse dans le calcul à droite du centre par opposition à la gauche. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 1. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
PolynomialOrder |
Indique l'ordre du polynôme qui est ajusté localement à l'ensemble de données et donc utilisé pour déterminer les coefficients de filtrage. L'ordre polynomial choisi doit être inférieur à la largeur de lissage (de sorte qu'un nombre suffisant de points de données soit disponible pour l'ajustement du polynôme local). Sinon, l'ordre polynomial pour le calcul est réduit à SmoothingWidth - 1. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 0 et inférieure ou égale à 15. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 2 . |
Extrapolate |
La valeur TRUE indique que les points limites doivent être étendus symétriquement pour le filtrage. Dans ce cas, les coefficients de filtrage ne doivent être calculés qu'une seule fois. L'extrapolation peut certes entraîner un comportement irrégulier du lissage sur les bords, mais l'algorithme reste rapide. Si FALSE est sélectionné, le même ordre polynomial est utilisé pour lisser les points limites. Dans ce cas, la largeur de lissage et l'ordre du polynôme à ajuster restent les mêmes aux points marginaux, tandis que le centre du filtre est déplacé en direction des marges. Dans ce cas, les coefficients de filtrage doivent être calculés individuellement pour tous les points limites. Cela permet généralement d'obtenir une plus grande précision lors du lissage des bords, mais l'algorithme est considérablement plus lent. Les structures de données autorisées sont Scalaire. Les types de données pris en charge sont Valeur booléenne. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut TRUE . |
Remarques
Le résultat a la même structure et la même unité que l'argument DataSet.
Chaque valeur dans DataSet est lissée avec (SmoothingWidth-1)/2 valeurs voisines de gauche et (SmoothingWidth-1)/2 valeurs voisines à droite (lorsque SmoothingWidth est inégale). Le lissage correspond à la convolution du signal avec des coefficients de filtrage de longueur SmoothingWidth. Pour cette procédure, les coefficients du filtre sont déterminés de telle sorte que le résultat corresponde à une régression polynomiale locale (c'est-à-dire un ajustement de la courbe polynomiale locale). Les coefficients du filtre ne dépendent pas des valeurs y. L'algorithme est décrit dans Algorithme SavitzkyGolay.
Le filtrage n'est pas optimisé pour la suppression des hautes fréquences, mais pour la suppression des moments statistiques d'ordre supérieur. Le filtre est donc particulièrement adapté au lissage des signaux qui, sans bruit, auraient une plage de fréquences élevée. La méthode est également utilisée lorsqu'un pic a été échantillonné à travers quelques points seulement. La position et la hauteur du pic peuvent être estimées, même si le maximum se situe entre deux points de prélèvement. Une application typique comprend, par exemple, l'analyse des spectres infrarouges. La méthode de lissage Savitzky-Golay est également connue sous le nom de filtre polynomial de lissage numérique (DISPO) et de lissage des moindres carrés.
Avant le filtrage, les valeurs sont converties en valeurs réelles ou complexes à virgule flottante de 64 bits. Le type de données du résultat est toujours une valeur réelle ou complexe à virgule flottante de 64 bits.
L'illustration montre la différence entre les deux fonctions de lissage Smooth (moyenne glissante) et SavitzkyGolayFilter (avec un ordre polynomial de 4). Les deux fonctions ont la même largeur de lissage. Alors que dans le lissage de Savitzky-Golay, le pic le plus large est moins lissé par rapport à la moyenne mobile, les pics plus étroits conservent leurs hauteurs et leurs largeurs.
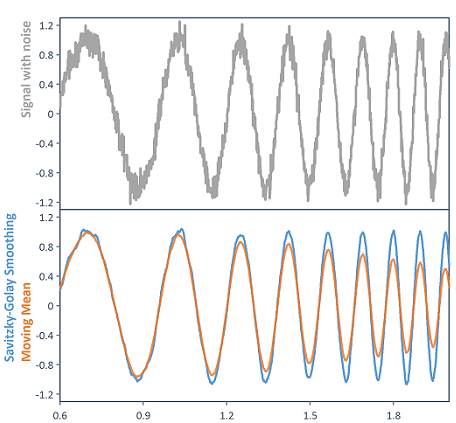
Disponible dans
Option Filtres numériques
Exemples
SavitzkyGolayFilter(Signal, 7, 2)
Lisse un signal en utilisant le filtre Savitzky-Golay. Pour ce faire, on utilise un polynôme du deuxième degré et on inclut dans le résultat trois valeurs voisines à gauche et à droite de chaque valeur à lisser (c'est-à-dire 7 valeurs au total).
SavitzkyGolayFilter(DataSet, N, 0)
Lisse un ensemble de données avec le filtre de Savitzky-Golay en ajustant localement la courbe avec un polynôme d'ordre 0. Cela correspond à une moyenne mobile. À l'exception des points limites, le code est donc équivalent à Mean(DataSet, MEAN_ARITHMETIC + CALC_MOVING, N).
Dim N = 10
Dim polyOrder = 4
Dim width = 2*N + 1
Dim dirac = (0 # width) : 1 : (0 # width)
Dim coeff = SavitzkyGolayFilter(dirac, width, polyOrder)[N + 1, N + width]
AmplitudeResponse(coeff)
Calcule la réponse en amplitude du filtre de Savitzky-Golay (pour un polynôme d'ordre 4 et une largeur de lissage de 21). Pour ce faire, la fonction SavitzkyGolayFilter est appliquée à une impulsion de Dirac. On obtient ainsi la fonction de transfert du système sous la forme de coefficients de filtre. À l'aide des coefficients de filtrage, la fonction AmplitudeResponse permet de calculer la réponse en amplitude du filtre.
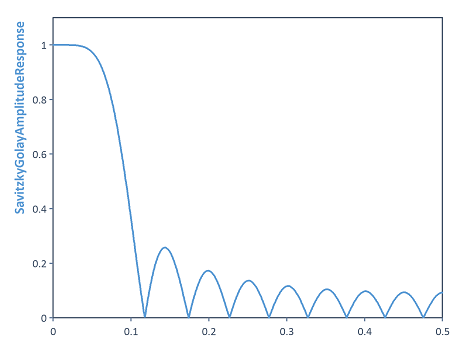
Voir aussi
Fonction SavitzkyGolayDerivative
Objet d'analyse Lissage de Signal
Littérature
[1] Savitzky, A.; Golay, M.J.E.: Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Dans: Analytical Chemistry, Vol. 36, No. 8, Pages 1627-39. http://pubs.acs.org/doi/abs/10.1021/ac60214a047, le 1964.
[2] A. Gorry: General least-squares smoothing and differentiation by the convolution (Savitzky–Golay) method. Dans: Analytical Chemistry, Vol. 62, No. 2, Pages 570-3. http://pubs.acs.org/doi/abs/10.1021/ac00205a007, le 1990.