Filtre un signal avec un filtre gaussien. Généralement utilisé pour le lissage et comme filtre pour mesurer et analyser la circularité.
Syntaxe
GaussianFilter(DataSet, le Type, le Fc1, le [ Fc2 ], le [ SamplingRate ] [ , le Mode Variable GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION ])
La syntaxe de la fonction GaussianFilter se compose des éléments suivants :
Section |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
L'ensemble de données à filtrer. Les structures de données autorisées sont Série de données, le Matrice de données, le Signal et Série de signaux. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. Les valeurs invalides ne sont pas autorisées dans cet argument. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||||||
Type |
Précise le type de filtre. L'argument Type peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||
Fc1 |
Spécifie la première fréquence de coupure du filtre gaussien. La fréquence doit être comprise entre 0 et 0,5 (la moitié du taux d'échantillonnage normalisé à un) ou entre 0 et 0,5 * SamplingRate.Pour le filtre gaussien, la fréquence de coupure est définie comme la fréquence à laquelle l'amplitude du filtre passe par 50 % de l'amplitude initiale du signal. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure ou égale à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||
Fc2 |
Spécifie la seconde fréquence de coupure du filtre gaussien. La fréquence doit être comprise entre 0 et 0,5 (la moitié du taux d'échantillonnage normalisé à un) ou entre 0 et 0,5 * SamplingRate. Cet argument n'a pas à être spécifié pour un filtre passe-bas ou passe-haut.Pour le filtre gaussien, la fréquence de coupure est définie comme la fréquence à laquelle l'amplitude du filtre passe par 50 % de l'amplitude initiale du signal. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure ou égale à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||
SamplingRate |
Précise le taux d'échantillonnage. L'argument est facultatif. Si l'argument n'est pas spécifié, il faut, pour les fréquences de coupure Fc1 et Fc2 une fréquence normalisée de 0 à 0,5 doit être indiquée pour chacun d'eux. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. La valeur doit être supérieure à 0. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||||||
Mode |
Le filtrage correspond à la convolution (rapide) avec une fonction gaussienne dans le domaine temporel. L'argument précise donc le mode de calcul pour effectuer la convolution. L'argument Mode peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION . |
Remarques
Le filtre gaussien (passe-bas) correspond à la convolution avec la fonction gaussienne suivante (noyau de convolution) dans le domaine temporel :
Dans cette équation, fc représente la fréquence de coupure. Dans ce cas, la convolution est calculée à l'aide de la FFT (transformée de Fourier rapide) comme suit : Comme la transformée de Fourier rapide d'une fonction gaussienne produit à son tour une fonction gaussienne, la fonction de transfert (c'est-à-dire FFTn(GaussianKernel)) peut être calculée explicitement. Dans le domaine fréquentiel, le filtre est donc calculé comme une multiplication avec la fonction de transfert suivante :
En sélectionnant f = fc, on obtient S(f) = 0,5, c'est-à-dire que l'amplitude du filtre passe par 50 % de l'amplitude du signal d'origine.
Dans le domaine fréquentiel, le filtre passe-haut gaussien correspond à une multiplication avec la fonction de transfert 1-S(f). Le filtre passe-bande et coupe-bande résulte en conséquence de la combinaison d'un passe-bas et d'un passe-haut.
Pour le choix particulier suivant de fc, le noyau gaussien dans le domaine temporel s'écrit de manière équivalente comme une convolution avec une distribution normale gaussienne (avec une valeur attendue de 0 et un écart-type de σ) sous forme de
La structure du résultat correspond à celle de l'argument DataSet. Pour les matrices de données et les séries de signaux, le calcul s'effectue colonne par colonne. Les composantes X ou Z, si elles sont présentes, sont reprises telles quelles dans le résultat.
Remarque Le filtre gaussien peut notamment être utilisé pour le lissage. Il est également souvent utilisé comme filtre pour les mesures de circularité ou les analyses de circularité, voir [1]. Le mode GAUSSIANFILTERMODE_PERIODIC_BOUNDARY doit être utilisé dans ce cas s'il s'agit d'un ensemble de données d'entrée périodique ou d'un profil de circularité fermé. Pour les données non périodiques et les données transitoires, le mode GAUSSIANFILTERMODE_ZERO_BOUNDARY doit être utilisé (correspond à la condition de bord zéro). À cette fin, un nombre approprié de zéros est ajouté au signal d'entrée pour la transformée de Fourier (zero padding). Pour les données non périodiques avec une condition limite inconnue, le mode GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION (condition limite exacte inconnue, les données sont prolongées de manière symétrique). En règle générale, cela permet d'obtenir un lissage naturel des bords.
Disponible dans
Option Filtres numériques
Exemples
GaussianFilter(Data, FILTER_LOWPASS, 0.04)
Lisse un ensemble de données à l'aide d'un filtre passe-bas gaussien avec une fréquence de coupure de 0,04. Fournit généralement un lissage plus important qu'avec un lissage à moyenne mobile à l'aide de la fonction Smooth.
GaussianFilter(Data, FILTER_HIGHPASS, 0.01)
Supprime la composante continue avec un filtre passe-haut gaussien à faible fréquence de coupure. Renvoie un résultat similaire à celui de la fonction DCRemovalFilter.
Dim dirac = (0 # 100) : 1 : (0 # 100)
Dim gaussCoeff = GaussianFilter(dirac, FILTER_LOWPASS, 0.04)
AmplitudeResponse(gaussCoeff)
Calcule la réponse en amplitude du filtre gaussien (passe-bas avec une fréquence de coupure de 0,04). Pour ce faire, la fonction GaussianFilter est appliquée à une impulsion de Dirac. On obtient ainsi la fonction de transfert du système sous la forme de coefficients de filtre. À l'aide des coefficients de filtrage, la fonction AmplitudeResponse permet de calculer la réponse en amplitude du filtre. La figure suivante montre la comparaison de la réponse en amplitude du filtre passe-bas de Gauss avec une fréquence de coupure de 0,04 à une moyenne mobile avec une largeur de lissage de 7 (voir fonction Smooth). Les hautes fréquences, en particulier, sont mieux supprimées que lorsque l'on utilise la moyenne glissante :
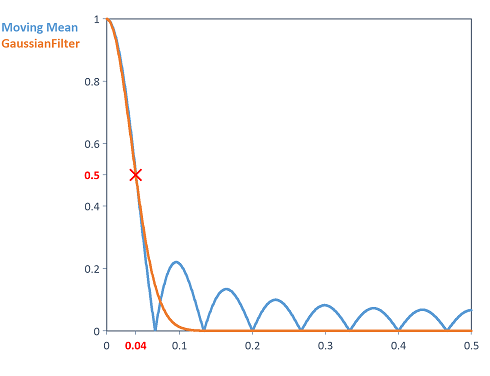
La figure suivante montre la comparaison de la réponse en amplitude du filtre passe-haut de Gauss avec une fréquence de coupure de 0,04 et de la fonction DCRemovalFilter avec la même fréquence de coupure et d'ordre 2 :
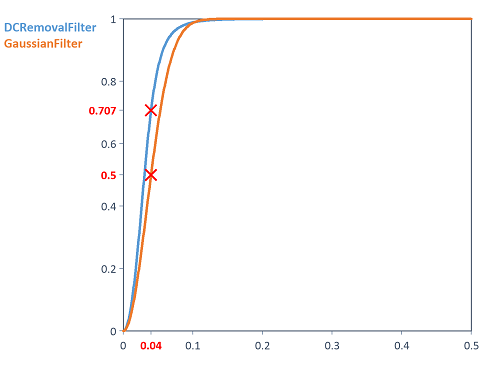
Dim sigma = 4.5
Dim fc = sqrt(log(2))/(sigma*sqrt(2)*PI)
GaussianFilter(Data, FILTER_LOWPASS, fc)
Lisse un ensemble de données par convolution avec une distribution normale gaussienne avec un écart-type réglable de σ (largeur).
Voir aussi
Fonction MaximumInscribedCircle
Fonction MinimumCircumscribedCircle
Objet d'analyse Lissage de Signal
Objet d'analyse Approximation Circulaire
Littérature
[1] B. Muralikrishnan, J. Raja: Computational Surface and Roundness Metrology. Springer-Verlag London Limited, 2009. ISBN 1-848-00296-3.
[2] DIN Deutsches Institut für Normung e.V.: Part 2: Specification operators (ISO 12181-2:2011); English translation of DIN EN ISO 12181-2:2011-07. Dans: Geometrical product specifications (GPS) - Roundness. 2011.