Calcule diverses fonctions de distribution ou de densité.
Syntaxe
Distribution(X, le Distribution, le Parameter1 [ , le Parameter2 ])
La syntaxe de la fonction Distribution se compose des éléments suivants :
Section |
Description |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
X |
Contient les valeurs X, c'est-à-dire les valeurs de la variable aléatoire pour laquelle la fonction de distribution ou la fonction de densité doit être calculée. Lors du calcul d'une distribution discrète, les valeurs X doivent être intégrales et positives. Les structures de données autorisées sont Scalaire, le Série de données et Matrice de données. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||||||||||||||||||
Distribution |
Précise quelle distribution doit être calculée et si la fonction de distribution ou la fonction de densité doit être calculée. L'argument Distribution peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||||||||||||||
Parameter1 |
Spécifie le premier paramètre de la distribution à calculer. Les structures de données autorisées sont Scalaire. Tous les types de données numériques sont autorisés. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||||||||||||||||
Parameter2 |
Si nécessaire, précise le deuxième paramètre de la distribution à calculer. Les structures de données autorisées sont Scalaire. Tous les types de données numériques sont autorisés. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
Remarques
Le résultat est toujours du type de données Virgule flottante de 64 bits.
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution normale avec une valeur d'espérance μ et une variance σ² sont données par :
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la loi logarithmique normale avec les paramètres μ et σ² sont données par :
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution exponentielle avec le paramètre α (paramètre d'échelle inverse) sont données par :
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution de Weibull avec les paramètres α et β (paramètres de forme) sont données par :
Remarque : dans la littérature, la durée de vie caractéristique T est souvent utilisée comme alternative au paramètre α (et β est désigné par k). La relation suivante s'applique :
De même, dans la littérature, le paramètre d'échelle inverse λ = 1/T est souvent utilisé à la place du paramètre α. La règle est donc la suivante :
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution du khi-carré avec le paramètre n (nombre de degrés de liberté) sont données par :
P(n1,n2) désigne ici la fonction gamma régularisée et incomplète.
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution de Student-t avec le paramètre n (nombre de degrés de liberté) sont données par :
I(z,n1,n2) désigne ici (et dans la suite) la fonction bêta incomplète régularisée.
La densité de probabilité continue f(x) et la fonction de répartition F(x) de la distribution F (distribution de Fisher) avec les paramètres m (nombre de degrés de liberté au dénominateur) et n (nombre de degrés de liberté au numérateur) sont données par :
La densité de probabilité discrète f(k) et la fonction de répartition F(x) de la distribution binomiale avec les paramètres n (nombre d'essais) et p (probabilité de succès ou de réussite) sont données par :
La densité de probabilité discrète f(k) et la fonction de répartition F(x) de la distribution de Poisson avec le paramètre λ (taux d'événements moyen) sont données par :
Disponible dans
Option Statistiques
Exemples
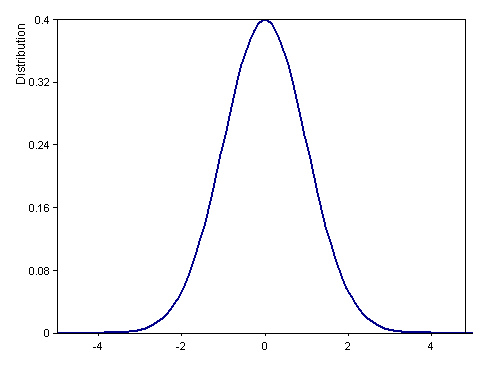
Dim x = Series(-5, 5, 0.05)
Signal(Distribution(x, DISTRIBUTION_NORMAL + DISTRIBUTION_DENSITY, 0, 1), x)
Calcule la fonction de densité de la distribution normale standard (moyenne 0, variance 1) dans l'intervalle [-5, 5].
Voir aussi
Fonction EmpiricalDistribution
Littérature
[1] "Hartung, Joachim": "Statistik, 9. Auflage". "Oldenbourg Verlag GmbH, München", 1993. ISBN 3-486-22055-1.