Calcul du signal analytique
Définir l'amplitude instantanée, la phase instantanée et la fréquence instantanée
En transformant le signal d'entrée réel en un signal analytique, il est possible de dériver et d'examiner les quantités locales du signal original, l'amplitude instantanée, la phase instantanée et la fréquence instantanée :
À cette fin, écrivez le signal analytique z(t) dans un graphique polaire comme suit :
L'amplitude instantanée ou l'enveloppe instantanée est maintenant définie comme l'amplitude a(t) du signal analytique ; c'est-à-dire :
Si le signal d'origine ne présente pas de tendance ou de décalage, il s'agit en fait de la réponse en amplitude ou de l'enveloppe supérieure du signal à analyser.
La phase instantanée est la phase du signal Φ(t). La phase Φ(t) peut être modélisée sous la forme suivante :
La fréquence instantanée ω(t) est donc définie comme suit : :
Pour les signaux à composante unique sans tendance ni décalage, ces définitions donnent en fait la réponse en phase ainsi que la réponse en fréquence du signal à analyser.
Pour les signaux qui ont une tendance ou un décalage, toutes les interprétations mentionnées ci-dessus ne sont correctes que lorsqu'une correction de la tendance du signal est effectuée. L'exemple suivant clarifie ces relations :
Reportez-vous également à [2] et [3] pour plus d'informations.
Applications : Calcul de l'amplitude instantanée, de la phase instantanée, de la fréquence instantanée et de l'enveloppe
Remarque : La liste suivante de formules FPScript utilisées pour calculer l'amplitude instantanée, la phase instantanée et la fréquence instantanée constitue la base de l'Objet d'analyse Grandeur instantanée. L'exemple suivant peut donc être évalué de manière similaire avec l'Objet d'analyse Grandeur instantanée.
Pour l'exemple, vous générez d'abord un cosinus de fréquence balayée avec 10 000 valeurs dont la composante X a l'unité s, commençant à 0 s et finissant à 20 s. La fréquence de départ est de 5 Hz et la fréquence d'arrivée est de 15 Hz. L'amplitude du cosinus de la fréquence balayée est de 1, le décalage et la phase de départ sont chacun de 0. Maintenant, mettez à l'échelle le signal synthétique généré à l'aide de la formule suivante (appelée Data) :
Dim amplitude = Sqrt(Value Signal.X + 1)
amplitude * Signal
Le spectre temps-fréquence du signal mis à l'échelle (visualisé dans un graphique de contour 3D) renvoi :
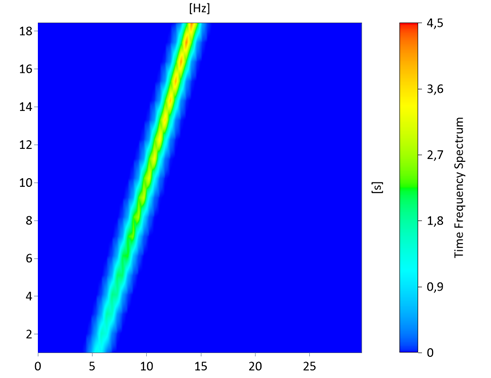
Le signal n'a pas de tendance. Le format pour le calcul de l'amplitude instantanée est donc le suivant :
Absolute(AnalyticSignal(Data))
Comme mentionné ci-dessus, cela correspond maintenant à l'enveloppe supérieure (ou la réponse en amplitude) du signal mis à l'échelle :
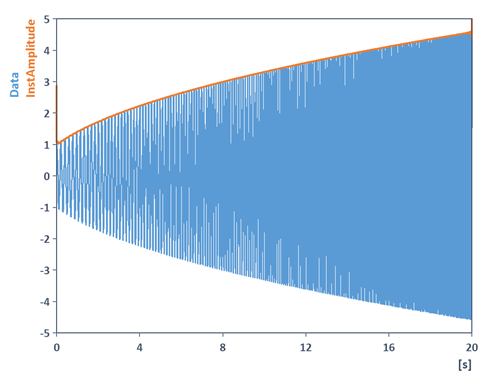
L'enveloppe inférieure est obtenue de manière similaire en utilisant :
-Absolute(AnalyticSignal(Data))
Pour calculer la fréquence instantanée, utilisez le code FPScript suivant :
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(Data)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
On obtient ainsi la réponse en fréquence du signal :
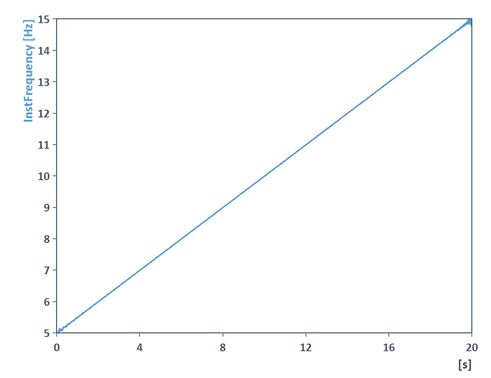
Créez maintenant une deuxième formule (appelée DataWithOffset) dans laquelle un décalage ou une tendance est ajouté : Exemple :
Data + 35
Remarque : pour déterminer la réponse en amplitude, la réponse en phase, la réponse en fréquence ou l'enveloppe (à l'aide des algorithmes ci-dessus), il est nécessaire de corriger la tendance ou le décalage du signal à analyser.
Recalculez d'abord l'amplitude instantanée. Par exemple, la correction de tendance peut être effectuée à l'aide de la fonction FPScript Trend ou par le biais de valeurs moyennes glissantes à l'aide de la fonction Mean :
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset))
Cela se traduit en fait par la réponse en amplitude du signal mis à l'échelle avec un décalage. Cependant, pour déterminer l'enveloppe, il faut ensuite réintégrer la tendance. La formule doit seulement être légèrement modifiée comme suit :
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset)) + offset
Cela renvoie en fait l'enveloppe supérieure du signal mis à l'échelle avec un décalage :
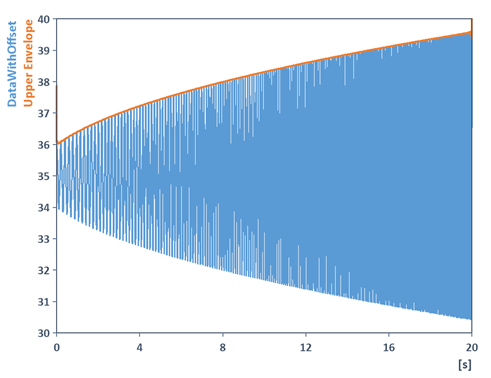
Notez que pour déterminer la réponse en fréquence, il est nécessaire de soustraire également le décalage :
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(DataWithOffset - offset)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
Note 1 : Lors du calcul de l'amplitude instantanée, de la phase instantanée, de la fréquence instantanée ou de l'enveloppe, sur les bords du signal (ou généralement à proximité des discontinuités de saut du signal), des effets secondaires sous forme de dépassements peuvent se produire. Ces dépassements ne peuvent être évités dans l'algorithme susmentionné et sont déterminés de manière purement mathématique. La cause en est le phénomène de Gibbs, qui provoque des dépassements au voisinage des discontinuités de saut dans le cas des séries de Fourier et de la transformée de Fourier.
Note 2 : Pour le signal suivant fourni avec les données d'exemple de FlexPro, l'algorithme susmentionné pour déterminer les enveloppes supérieures (avec correction de tendance à l'aide de la fonction Mean) donne l'enveloppe supérieure. Il n'est pas nécessaire que le signal soit un signal à une seule composante :
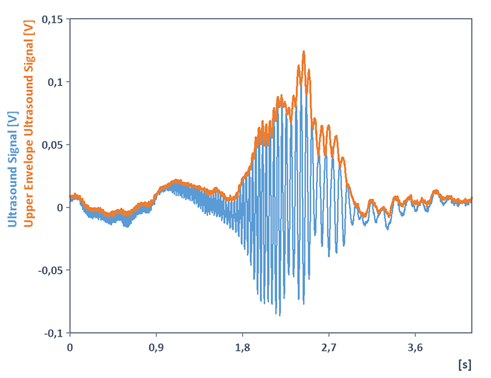
Note 3 : Il est important de noter que dans le cas de signaux multi composants, les interprétations comme phase instantanée et fréquence instantanée ne s'appliquent plus. Notez le code FPScript suivant pour cela :
Dim x = Series(0 s, 1 s, 0.001)
Dim y = Sin(2 * PI * x * 30 Hz) + Sin(2 * PI * x * 90 Hz)
Signal(y,x)
Dans ce cas, l'algorithme de détermination de la fréquence instantanée aboutit à une moyenne des deux fréquences sinusoïdales :
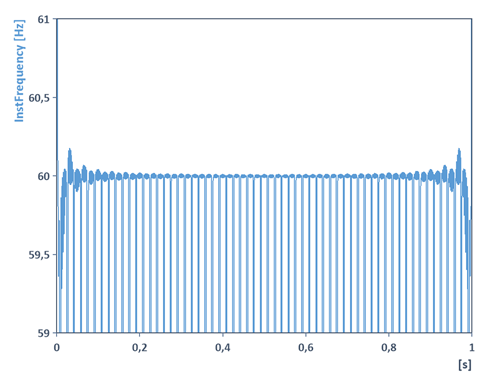
Application supplémentaire : Démodulation des signaux (démodulation d'amplitude, démodulation de phase, démodulation de fréquence)
Les grandeurs instantanées ainsi définies peuvent donc également être utilisées pour la démodulation des signaux. Par exemple, un signal modulé est fourni comme suit :
L'amplitude instantanée se traduit alors par la réponse en amplitude a(t), tandis que la phase instantanée est calculée comme Φ(t). En outre, la réponse en fréquence du signal spécifié peut être déterminée à l'aide de la fréquence instantanée.
Contexte théorique : L'algorithme de calcul du signal analytique.
L'algorithme à temps continu susmentionné définit la fonction de transfert H dans le domaine fréquentiel. L'algorithme de calcul du signal analytique discret est donc (avec l'aide de la FFT et de la fonction de transfert discrète H) mis en œuvre comme décrit ci-dessous ; se référer notamment à [1] :
La fonction de transfert est spécifiée pour les longueurs de FFT paires comme : H[k] = 2 pour k = 1, 2, ..., FFTLength/2 - 1 (fréquences positives) et H[k] = 0 pour k = FFTLength/2 + 1, ..., FFTLength (fréquences négatives). Les coefficients symétriques k = 0 et k = FFTLength/2 sont spéciaux. Pour ceux-ci, H[k] = 1.
La fonction de transfert est spécifiée de la même manière que pour les longueurs de FFT inégales : H[k] = 2 pour k = 1, 2, ..., (FFTLength-1)/2 et H[k] = 0 pour k = (FFTLength-1)/2 + 1, ..., FFTLength ainsi qu'en plus H[0] = 1.
L'algorithme FPScript de calcul du signal analytique est donc défini comme suit (l'argument FFTLength doit être supérieur ou égal à la longueur des données) :
Arguments sig, FFTLength
Dim N = NumberOfRows(sig)
Dim fftInput = ComplexFloatingPoint64(sig.Y : (0 # (FFTLength - N)))
Dim fourierTrafo = FFTn(fftInput)
Dim H = 0 # FFTLength
H[0] = 1
If FFTLength Mod 2 == 0 Then
H[FFTLength/2] = 1
H[1, FFTLength/2 - 1] = 2
Else
H[1, (FFTLength - 1)/2] = 2
End
return Signal(IFFTn(H * fourierTrafo)[0, N-1], sig.X)
Influence de la longueur de la FFT : En utilisant un rajout de zéro (zero padding), c'est-à-dire en sélectionnant une longueur de FFT supérieure à la longueur des données, la résolution de la FFT requise pour l'algorithme est augmentée. Le résultat du calcul peut ainsi être amélioré. Vous en trouverez un exemple dans l'aide en ligne consacrée à la fonction Hilbert.
Références
[1] S. Lawrence Marple, Jr., "Computing the Discrete-Time "Analytic" Signal via FFT", IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222,1999.
[2] B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono, "On Instantaneous Amplitude and Phase of Signals", IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833,1997.
Voir aussi
Objet d'analyse Grandeur instantanée
