Este tutorial aborda el análisis espectral de Fourier en FlexPro para datos no estacionarios. Esto incluye tanto la Transformada de Fourier de tiempo corto (STFT) como la transformada de ondícula continua (CWT). Estos procedimientos son útiles para analizar las propiedades cambiantes de un conjunto de datos. También se pueden identificar regiones estacionarias para el análisis de Fourier convencional y el análisis espectral paramétrico.
Una señal de prueba con cuatro curvas senoidales secuenciales
Este tutorial utiliza un conjunto de datos no estacionarios con cuatro rangos, cada uno de los cuales contiene una curva senoidal con una frecuencia diferente.
Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Spectral Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Spectral Analysis.fpd. Abra la carpeta Tutorials y la subcarpeta Time-Frequency Analysis y haga doble clic para abrir el diagrama 2D Data.
Es la imagen de la señal que contiene 1024 valores en coma flotante.
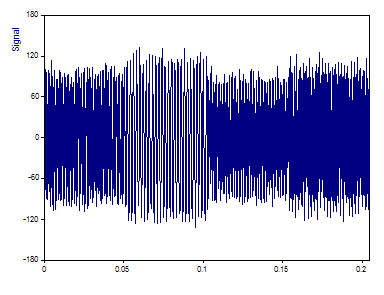
Los valores x (tiempo) varían de 0 a 0,2047 con un intervalo de muestreo de 0,0002. La frecuencia de Nyquist es, por tanto, de 2500 Hz (la mitad de la frecuencia de muestreo de 5000 Hz). Las cuatro curvas senoidales se generaron con las siguientes amplitudes, frecuencias y fases:
100.0*sin(2π*x*1000)+
120.0*sin(2π*x*500+π/2)+
90.0*sin(2π*x*2000+π)+
110.0*sin(2π*x*1500+3π/2)
Se ha añadido un 10 % de ruido blanco aleatorio, es decir, el nivel de ruido de fondo es de -20 dB.
La pérdida de información temporal en la transformada de Fourier.
Empiece observando el espectro de Fourier simple de este conjunto de datos.
Cierre el diagrama y seleccione el conjunto de datos Signal.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis de Fourier en Análisis espectral. Seleccione Espectro de Fourier. Pulse el botón Siguiente.
Seleccione Amplitud como Tipo de espectro. Seleccione Rectángulo -13 dB W=1 como Tipo de ventana. Asegúrese de que la Longitud de la FFT está ajustada a la longitud de datos o a 1024. Seleccione la opción Número máximo de picos e introduzca el valor 4. A continuación, establezca Límite crítico ruido blanco % en Ninguno. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
La visualización del espectro de Fourier en el asistente para análisis debería tener este aspecto:
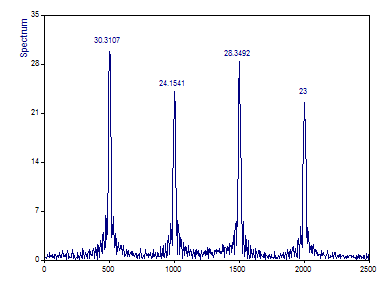
Aunque el espectro de Fourier identifica correctamente las frecuencias de los cuatro componentes secuenciales, no hay ninguna indicación de dónde empiezan o acaban estos armónicos en el dominio del tiempo. Se ha perdido toda la información sobre el dominio del tiempo, ya que cada componente asume una duración temporal infinita.
Dado que cada uno de los componentes solo es visible durante aproximadamente una cuarta parte de la longitud total del conjunto de datos, cada amplitud tiene aproximadamente solo una cuarta parte del valor real del armónico transitorio.
Una señal debe ser estacionaria en sentido amplio para ser adecuada para un espectro de Fourier. Esto significa que los espectros deben ser constantes tanto en frecuencia como en potencia a lo largo del período de muestreo. Tanto la CWT como la STFT son más adecuadas para analizar señales no estacionarias, ya que proporcionan un espectro de tiempo-frecuencia de los datos.
Espectro de la transformada rápida de Fourier
La Transformada de Fourier de tiempo corto (STFT) es similar al periodograma o a la FFT de segmentos solapados, salvo que a cada segmento se le asigna el valor central de tiempo que corresponde a su posición temporal en la serie de datos. Mientras la amplitud o la potencia no tengan que determinarse directamente a partir de los picos, normalmente se utiliza una ventana de ponderación para lograr la mejor localización temporal posible.
Los espectros de tiempo-frecuencia son intrínsecamente borrosos. Cuanto mejor sea la resolución del tiempo, peor será la resolución de la frecuencia y viceversa. La STFT es la mejor manera de hacerse una idea de este efecto.
Haga clic en el botón Atrás para ir al paso 1 del asistente para análisis. Seleccione la categoría Análisis tiempo-frecuencia y, a continuación, STFT. Haga clic en Siguiente para ir al paso 2. El procedimiento Transformada de Fourier de tiempo corto (STFT) ya está seleccionado automáticamente.
Seleccione dB, normalizado como Tipo de espectro. Ajuste el tipo de ventana a Cos2 Hanning -31 dB W=2. Los valores por defecto se seleccionan como punto de partida. Asegúrese de que la longitud de la FFT está ajustada a la Longitud del segmento, la Longitud del segmento tiene el valor 256, que corresponde a un cuarto de la longitud de datos. Ajuste el Solapamiento en % a 50.
Para asignar el tiempo al eje x, como suele hacerse con los espectros de tiempo-frecuencia, seleccione Frecuencia es Z. Establezca el Rango máximo de dB en 20 y deje el Número máximo de valores de frecuencia STFT en ilimitado.
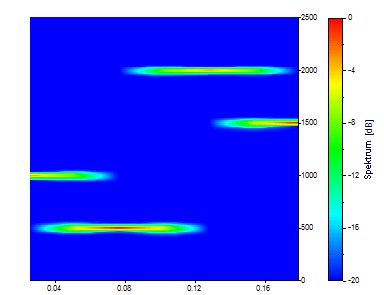
Estos ajustes producen siete instantáneas temporales, cada una de 0,05 segundos de duración. Hay 129 frecuencias. Si bien los componentes están muy definidos para las frecuencias 500, 1000, 1500 y 2000, no ocurre lo mismo en el eje temporal debido a la naturaleza secuencial de los armónicos. Dado que la hora asignada a una instantánea es también la hora del centro del segmento, en ambos extremos del intervalo de tiempo existe una amplia zona para la que no se dispone de información espectral.
Una forma sencilla de aumentar el número de puntos de tiempo es aumentar el valor de Solapamiento en %.
Cambie Solapamiento en % a 90.
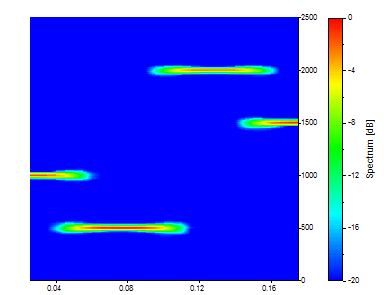
Ahora hay 31 instantáneas temporales diferentes que componen este espectro. Están disponibles las mismas 129 frecuencias. Aunque la resolución temporal experimenta una pequeña mejora, cada instantánea sigue representando de media más de una cuarta parte de los datos. Para mejorar la resolución temporal, hay que reducir la longitud del segmento.
Para reducir a la mitad la Longitud del segmento, introduzca el valor 128. Mantenga el Solapamiento en % en el valor 90.
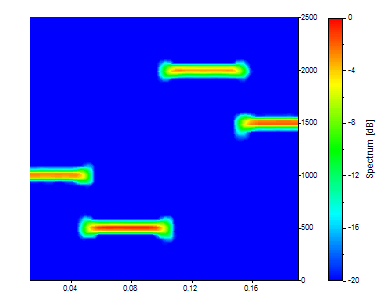
Ahora hay 75 segmentos temporales, cada uno de los cuales abarca una octava parte de los datos. Hay 65 frecuencias. El equilibrio entre el tiempo y la frecuencia debería ser evidente. Ahora hay mayor precisión en el dominio del tiempo, pero la resolución en frecuencia se ha deteriorado notablemente.
Cambie la Longitud del segmento a 64.
Mantenga el Solapamiento en % en el valor 90.
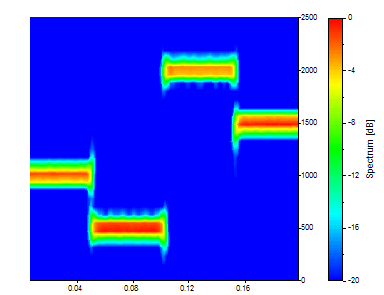
Ahora hay 161 segmentos temporales, cada uno de los cuales abarca una dieciseisava parte de los datos. Hay 33 frecuencias. La nitidez de la hora ha seguido mejorando, mientras que la resolución de la frecuencia se ha vuelto considerablemente más borrosa. Vaya un paso más allá y cambie la Longitud del segmento a 32. Mantenga el Solapamiento en % en el valor 90.
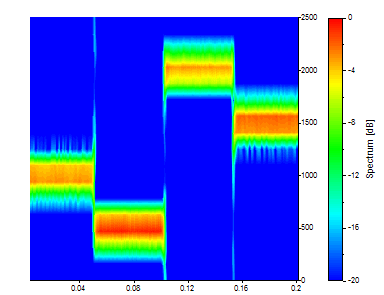
Ahora hay 331 valores de tiempo, pero solo 17 frecuencias. Las instantáneas temporales representan cada una treinta segundos de los datos. Por eso la limitación temporal es bastante nítida. En cambio, los picos del dominio de la frecuencia casi chocan.
La visualización se hace más clara en una visualización de superficie en 3D.
Haga clic en Vista estándar. Para mejorar la vista, cambie la longitud de la FFT a 128.
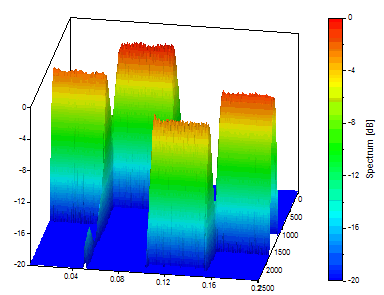
Esto muestra muy bien el equilibrio entre tiempo y frecuencia. Ahora vuelva a la configuración original que favorece la frecuencia.
Ajuste la Longitud del segmento a 256, la Longitud de la FFT a la Longitud del segmento y el Solapamiento en % a 90.
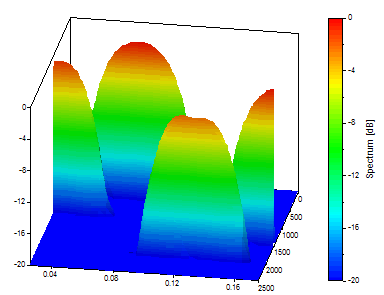
Esta presentación muestra la compensación tiempo-frecuencia con una buena resolución de frecuencia y un claro desenfoque temporal.
Optimizar los parámetros de la STFT puede ser todo un reto. La STFT es un análisis con una resolución fija. Aunque la STFT requiere un cuidadoso ajuste de los parámetros, puede utilizarse un espectro STFT para leer las amplitudes y potencias directamente como alturas de picos. Utilice una ventana de ponderación y ajuste la normalización a la amplitud o utilice una ventana rectangular junto con un solapamiento muy alto.
Obtendrá el siguiente gráfico si ajusta el Tipo de espectro a Amplitud, el tipo de ventana a Rectángulo -13 dB W=1 (sin ventana de ponderación), la longitud del segmento a 64, la Longitud de la FFT a 256 y el Solapamiento en % a 90.
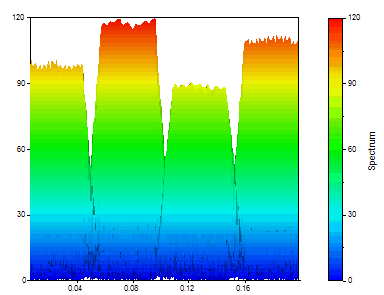
Transformada de ondícula continua
La STFT utiliza funciones senoidales desfasadas. La ausencia de restricciones temporales de las funciones sinoidales requiere la transformación de segmentos de ventana del conjunto de datos. Si las propias funciones elementales fueran de duración finita, se podría determinar un espectro a partir de la correlación entre las versiones desplazadas y estiradas/comprimidas de estas ondículas madre de duración finita y el conjunto de datos.
Este es el principio de la Transformada de ondícula continua (CWT).
A pesar del gran número de formas de ondículas, el uso de ondículas para el análisis espectral de tiempo-frecuencia suele ser más sencillo que optimizar la STFT. En la mayoría de los casos, las distintas ondículas madre y la configuración no tienen un efecto significativo en el resultado del espectro de tiempo-frecuencia. La selección de la ondícula madre y de los parámetros está vinculada al compromiso entre la resolución temporal y la frecuencial.
Seleccione Transformada de ondícula continua (CWT) y dB, normalizado como Tipo de espectro. Establezca el Tipo de ondícula en Morlet y el Ajuste (número de onda) en 8. Ajuste Rellenado con ceros a 1024 (rellena el conjunto de datos con 1024 valores hasta 2048 valores), el Número de frecuencias a 40 y deje la Frecuencia inicial en 0 y la Frecuencia final en 2500 (el rango de Nyquist completo). Asegúrese de que Frecuencia es Z está activado, que el Rango máximo de dB está ajustado a 20 y que Número máximo de valores de tiempo CWT tiene el valor 1024 (para registrar toda la longitud del conjunto de datos).
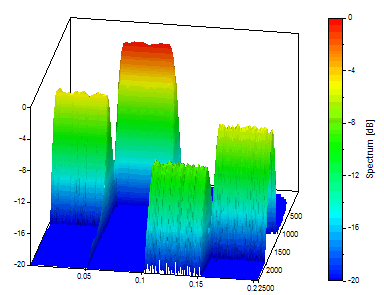
Este es un buen espectro de tiempo-frecuencia CWT. De hecho, se obtuvieron resultados respetables sin cambiar la ondícula madre ni el valor de su parámetro ajustable. Siempre se podría utilizar la ondícula Morlet con un número de onda de 8 y nunca se perderían las optimizaciones que resultarían de elegir la ondícula óptima y establecer su valor de ajuste para una resolución óptima de tiempo-frecuencia.
Para ver esto, ahora considerará los extremos que ofrece FlexPro.
Para revelar el equilibrio entre tiempo y frecuencia en el análisis de ondícula, se muestra de nuevo un diagrama de contorno. Haga clic en Vista en planta.
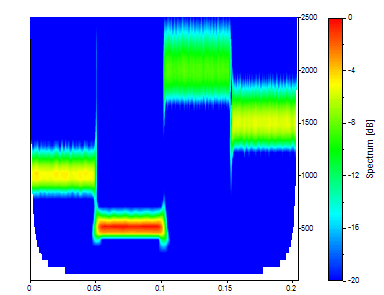
Cambie el Ajuste al número de onda 20.
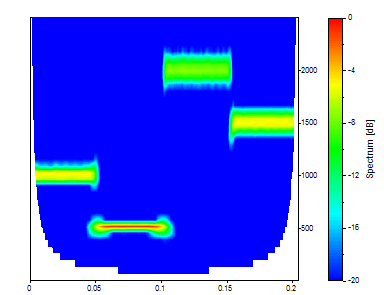
El Morlet con un parámetro ajustable (número de onda) de 20 genera una resolución de frecuencia más nítida, pero una peor localización temporal.
Cambie el Ajuste a 50.
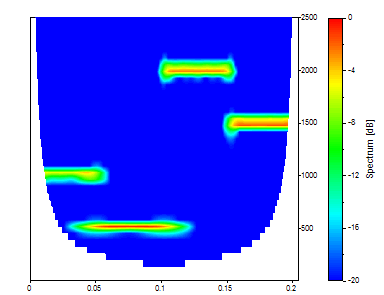
El Morlet con un número de onda de 50 produce una resolución de frecuencia muy alta, pero una localización temporal deficiente.
Establezca el tipo de ondícula en Derivada gaussiana y el valor de Ajuste en 2.
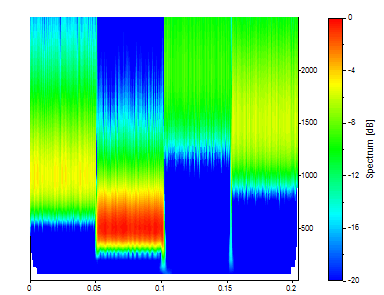
La ondícula derivada gaussianacon el parámetro ajustable 2 produce la localización temporal más nítida, pero una presentación de frecuencias muy borrosa.
"Análisis" multirresolución
La CWT es un método "multirresolución" tiempo-frecuencia. Si observa las figuras anteriores, se dará cuenta de que el pico con la frecuencia más baja tiene la mayor magnitud espectral CWT y es el menos "difuminado" en frecuencia de los cuatro componentes de la señal.
Esta propiedad es más un subproducto del algoritmo CWT que un objetivo en el desarrollo del algoritmo. El análisis "multirresolución" tiene ventajas e inconvenientes. Si los componentes de alta frecuencia se producen durante un breve período de tiempo, la mejor opción es sacrificar la resolución de frecuencia para resolver con precisión la aparición y desaparición del componente. Si los componentes de baja frecuencia son de larga duración, es mejor cambiar la resolución temporal por una mejor estimación de la frecuencia. Si estas afirmaciones son correctas, el análisis "multirresolución" de la CWT es una ganancia.
Si la persistencia es independiente de la frecuencia, o el objetivo principal es determinar las amplitudes y potencias directamente a partir de las magnitudes del espectro, el método de "multirresolución" no es ventajoso.
Redundancia de frecuencia de la CWT
A diferencia de la transformada de ondículas discreta (DWT), que suele utilizarse para el análisis de ondículas, la CWT puede analizarse a cualquier frecuencia. Estas frecuencias pueden dar lugar a cualquier grado de redundancia por solapamiento y pueden disponerse linealmente, logarítmicamente o de cualquier otra forma. Debido a que se debe guardar una FFT separada para cada frecuencia que se vaya a estimar, FlexPro limita el número total de frecuencias a 500. Gracias a esta redundancia de frecuencias, la CWT ofrece una resolución mucho mayor que la DWT.
Seleccione la ondícula Morlet con un número de onda de 12. Introduzca 100 como número de frecuencia, 400 como frecuencia inicial y 1200 como frecuencia final.
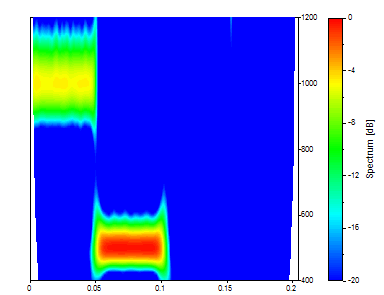
El análisis espectral CWT se centra ahora plenamente en la banda de frecuencias de 400 a 1200.
Rellenado con ceros en la FFT y efectos de borde
A diferencia del análisis de Fourier convencional, cuyo espectro se genera por transformación, la FFT utilizada en la CWT se emplea para la convolución rápida de ondículas escaladas y desplazadas con el conjunto de datos. Las funciones básicas de la CWT son ondículas escaladas y desplazadas, no funciones sinuidales y cosenoidales. El único propósito de añadir ceros a la CWT es evitar los efectos de aliasing durante la convolución rápida. Esto se evita completamente para todas las frecuencias si la longitud de la FFT es el doble que la longitud del conjunto de datos. A menudo tiene sentido añadir ceros hasta la siguiente potencia de 2 para suprimir los efectos de aliasing y, al mismo tiempo, lograr un cálculo rápido.
Si se utiliza una FFT de N exacta para la convolución rápida, el efecto de aliasing es claramente visible a bajas frecuencias. El efectos de aliasing disminuye al aumentar la frecuencia. Esto explica la ausencia de efectos de aliasing en el componente de frecuencia más alta. Si el contenido espectral a bajas frecuencias es despreciable o los datos de la sección considerada son periódicos, entonces no tiene sentido añadir ceros.
Si se utiliza la adición de ceros para evitar este efecto, se pierde el rendimiento asociado al efecto de aliasing. El resultado es un rendimiento reducido en los bordes del conjunto de datos. Esta zona de potencia reducida también se denomina "cone of influence" en la CWT. El "cone of influence" es especialmente claro cuando la separación de frecuencias es logarítmica.
Establezca el número de ondas Morlet en 100, el Rellenado con ceros en 0, el Número de frecuencias en 40, la Frecuencia inicial en 0 y la Frecuencia final en 2500.
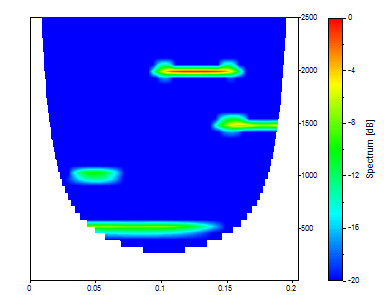
En este caso, un número de onda elevado proporciona un "cone of influence" mayor. El componente espectral con la frecuencia más baja se refleja aquí en el borde derecho de la escala temporal. Esto no se muestra en FlexPro, ya que la información en este "cone of influence" no se visualiza.
Establezca el número de onda Morlet en 12 y haga clic en Siguiente. Active las dos opciones del paso 3 y pulse el botón Finalizar.
Se crean cuatro objetos en la base de datos del proyecto FlexPro.
"Espectro" es el objeto de análisis. Realiza el análisis espectral y puede abrirse haciendo doble clic.
"Espectro" es la presentación del espectro de tiempo-frecuencia generado por el asistente para análisis. Utiliza el objeto "Espectro".
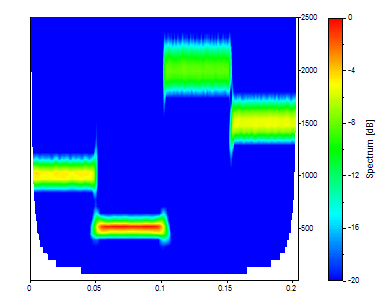
"Datos" es la presentación de los datos originales del dominio de tiempo.
"Tiempo-frecuencia" es un documento que contiene la presentación del espectro y los datos.
Bibliografía
Buenas introducciones al procesamiento digital de señales son:
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). Transmisión de señales. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Aquí se describen los algoritmos FFT utilizados en FlexPro:
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, pág. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust, v. AU-17, pág. 93, junio de 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, pág. 1249, mayo-junio de 1969
Encontrará información sobre las funciones de ventana en:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, feb. 1981.
Para quienes deseen comprender los entresijos del análisis de ondículas en la práctica, recomendamos consultar el siguiente documento:
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, v.79, no.1, pág. 61-78. enero de 1998
Este documento explica la CWT en el contexto del análisis de los valores temporales de El Niño. Los autores también han publicado el paquete FORTRAN (dominio público) WAVEPACK para el análisis de ondículas. Tanto el documento como el código WAVEPACK pueden consultarse en http://paos.colorado.edu/research/wavelets/.