Este tutorial trata sobre el análisis espectral de Fourier en FlexPro em el caso de que se deban analizar componentes con muy baja potencia de señales ampliamente estacionarias, y cuando se requieran estimaciones espectrales con baja varianza.
Una señal de prueba adecuada
Para este tutorial se utiliza una señal que contiene cuatro curvas senoidales con la misma potencia que se extienden por el rango de Nyquist y tres curvas senoidales de baja potencia situadas entre ellas. Los componentes de baja potencia están -40 dB, -50 dB y -60 dB por debajo de las curvas senoidales de referencia. Además, se añade ruido blanco para que el ruido de fondo sea de aproximadamente -75 dB. El objetivo de esta prueba es estimar la frecuencia y la potencia exactas de estos tres componentes de baja potencia. Otro aspecto será la determinación de la información de fase de estos componentes.
Las siete curvas senoidales tienen este aspecto:
1.0*sin(2π*x*1005+π/2)+ (0 dB)
1.0*sin(2π*x*2005+π/2)+ (0 dB)
1.0*sin(2π*x*3005+π/2)+ (0 dB)
1.0*sin(2π*x*4005+π/2)+ (0 dB)
0.01*sin(2π*x*1505+π/2)+ (-40 dB)
0.003162*sin(2π*x*2505+3π/2)+ (-50 dB)
0.001*sin(2π*x*3505+π) (-60 dB)
El valor X (tiempo) varía de 0 a 0,1 con un incremento de 0,0001. La frecuencia de Nyquist es, por tanto, 5000 (la mitad de la frecuencia de muestreo de 10000). Las cuatro curvas senoidales de referencia se extienden por el rango de Nyquist. La primera curva senoidal de baja potencia (-40 dB) tiene el 1 % de la amplitud de las curvas senoidales de referencia y el 0,01 % de la potencia de una de las curvas senoidales de referencia. La segunda curva senoidal de baja potencia (-50 dB) tiene el 0,001 % de la potencia de las curvas de referencia. La última curva de prueba (-60 dB) solo tiene el 0,1 % de la amplitud y el 0,0001 % de la potencia de las curvas de referencia. Se añadió ruido gaussiano (al 0,15 %) para crear un ruido de fondo de aproximadamente -75 dB. Por tanto, debería ser posible analizar incluso el componente de -60 dB mediante un análisis espectral adecuado.
Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Spectral Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Spectral Analysis.fpd. Abra la carpeta Tutorials y la subcarpeta Fourier Spectral Analysis y haga doble clic en Data para abrir el diagrama 2D.
Esta es la figura de la señal con 1001 valores en coma flotante.
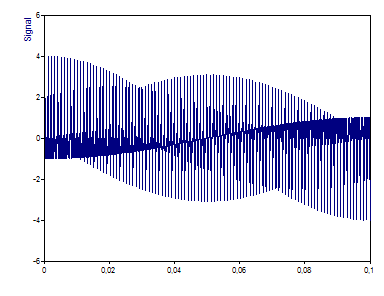
El espectro de Fourier no ponderado
Las funciones de ventana se utilizan casi siempre para el análisis espectral de Fourier con un alto rango dinámico. Para ver por qué es así, se observa primero un FFT simple, no ponderado.
Cierre el diagrama y seleccione el conjunto de datos Signal.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis de Fourier en Análisis espectrales. Allí se selecciona Espectro de Fourier. Pulse el botón Siguiente.
El paso 2 del asistente para análisis contiene un diálogo interactivo en el que se pueden optimizar y comparar varios procedimientos con el objetivo de lograr el mejor análisis posible. Comience observando el espectro de Fourier no ponderado.
Observe que la opción Espectro de Fourier está seleccionada en Procedimiento espectral. Aunque el Procedimiento espectral ya se seleccionó en el paso 1, puede modificarse en el paso 2.
Seleccione el valor dB, normalizado como el tipo de espectro.
Esto significa que el pico más alto del espectro se normaliza a 0 dB. Todos los demás picos tienen entonces un valor negativo. Un pico en -3 dB tendría la mitad de potencia que un pico a 0 dB y un pico a -6 dB tendría la mitad de amplitud.
Seleccione Rectángulo -13 dB W=1 como Tipo de ventana.
En el módulo de análisis espectral, todas las funciones de ventana fijas y no ajustables se enumeran por su nombre, la atenuación de los lóbulos laterales en dB y el ancho unilateral del lóbulo principal. Una ventana rectangular equivale a no aplicar ninguna ventana, ya que todos los elementos de datos se multiplican por uno.
Asegúrese de que la Longitud de la FFT está establecida en Longitud de datos o en 1001.
El campo de información Rellenado con ceros muestra que no se ha aplicado el rellenado con ceros (zero padding).
Seleccione Número máximo de picos en Opciones e introduzca el valor 7.
El asistente para análisis genera automáticamente información sobre los picos del espectro. Si la opción está ajustada a 7, se muestran los siete picos de mayor potencia. Tenga en cuenta que también es posible especificar un valor de umbral dB por debajo del pico más alto. Para este conjunto de datos podría establecer un valor umbral de -65 dB.
Ahora establezca Límite crítico ruido blanco % en Ninguno.
Más adelante experimentará con los límites críticos de la señal.
Si no hay ningún etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezcan el etiquetado de amplitud.
Puedes cambiar entre varios estados. Puede activar el etiquetado para el componente Y del espectro (aquí en dB, normalizado) o para el componente X (siempre frecuencias). También puede desactivar el etiquetado.
El gráfico de Fourier en el asistente para análisis debería tener este aspecto:
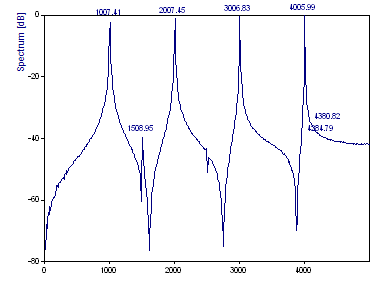
El cálculo FFT utiliza el algoritmo FFT más rápido posible, que transforma los datos con exactitud. En este caso, se utiliza el algoritmo FFT de factor primo porque es el procedimiento FFT más rápido que calcula el conjunto de datos con los 1001 valores. El espectro de Fourier generado capta los cuatro picos de referencia. Se asigna el pico de -40 dB. Solo hay un indicio del pico de -50 dB y ninguna señal del pico de -60 dB. Aunque las frecuencias de los picos del espectro se centran con una interpolación de spline cúbica, las frecuencias de referencia 1005, 2005, 3005 y 4005 no se reproducen con exactitud.
Observe que los cuatro picos de referencia tienen una forma claramente diferente. Los picos se hacen más pronunciados a medida que aumenta la frecuencia. Esto no es consecuencia de la frecuencia, sino del manchado espectral en las líneas de frecuencia vecinas del espectro. Cuanto más centrado esté un componente armónico dentro de las líneas de frecuencia, más nítida será la respuesta en frecuencia de la FFT.
Seleccione el gráfico superior y pulse el botón Activar cursor. Sitúe el cursor en el primer pico.
Tenga en cuenta que la frecuencia real del primer pico con el valor 1005 debe estar comprendida entre de las líneas de frecuencia FFT 999 y 1009. La frecuencia 4005 del cuarto pico puede acomodarse en gran medida en la línea de frecuencia FFT 4006. Solo si una frecuencia cae exactamente en una línea de frecuencia puede representarse un componente armónico mediante un único canal FFT.
Haga clic de nuevo en Activar cursor para desactivar el cursor. Cambie la Longitud de la FFT a 8192.
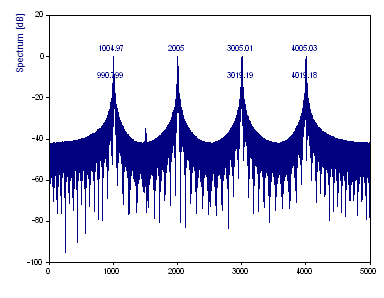
El espectro FFT se amplía mediante el rellenado con ceros. Ahora hay aproximadamente ocho veces más frecuencias dentro del espectro. Las frecuencias interpoladas de banda de las vibraciones de referencia se determinan ahora con precisión, pero los tres componentes de baja potencia se pierden en la línea de base. El manchado espectral aumenta a medida que el rellenado con ceros provoca una discontinuidad al final del conjunto de datos.
Introduzca 2000 en el campo Longitud de la FFT y fuerce una actualización saliendo del campo con la tecla Tab.
Esto genera un FFT con intervalos de espaciado exactos de 5 Hz. Las frecuencias de las siete curvas senoidales se encuentran ahora exactamente en el centro de una línea espectral FFT.
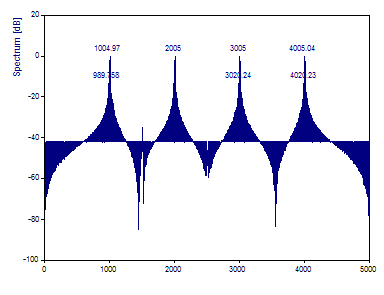
Los picos del espectro son ahora funciones de impulso, pero el manchado espectral causado por el rellenado con ceros es suficiente para ocultar los tres componentes de baja potencia. Sin una función de ventana, no es posible determinar los componentes de baja potencia.
Espectro de Fourier con función de ventana
Una función de ventana reduce la magnitud de valores de datos a 0 en cada extremo de un conjunto de datos. Mientras que esto aumenta la influencia de los datos en el centro de un conjunto de datos y reduce la influencia de los datos en el borde, elimina las discontinuidades en el borde de los datos. Si los datos se mostraran en un formato de visualización circular, la continuidad se observaría en el punto en el que se encuentran dos finales.
Una función de ventana también tiene efectos en el dominio de la frecuencia. La función de ventana tiene una respuesta en frecuencia que ensancha los picos de un espectro y, por tanto, reduce su resolución. También se introducen componentes armónicos de baja potencia. La ventaja es una reducción considerable de los efectos de fuga, lo que a su vez permite aplicar el rellenado con ceros en cualquier medida.
FlexPro realiza una normalización de la potencia cuando se utiliza una función de ventana. La potencia de un espectro de Fourier con función de ventana es idéntica a la potencia de su homólogo sin ponderar. Por otra parte, la altura de los picos del espectro disminuye ligeramente como consecuencia de la ventana a pesar de la normalización de la potencia. Si se utiliza una función de ventana, sigue siendo posible evaluar la potenica relativa utilizando la escala de dB normalizada. Pero ya no es posible leer las amplitudes o potencias absolutas directamente a partir de las alturas de los picos del espectro.
Cambie el Tipo de ventana a Cos4 Blackman-Harris -92 dB W=4 y establezca la Longitud de la FFT a 8192.
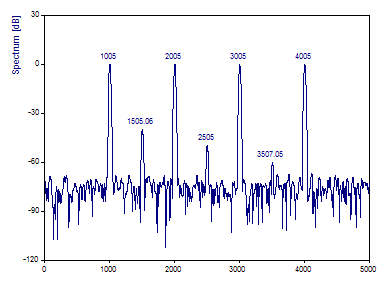
Haga clic en el botón Etiquetado para mostrar los valores absolutos de los espectros como etiquetas.
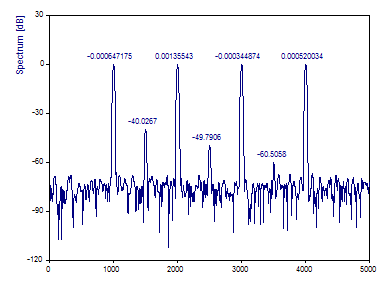
La ventana Blackman-Harris es muy popular para el análisis espectral de Fourier con un alto rango dinámico. Las siete curvas de referencia se trazan con exactitud tanto en términos de frecuencia como de potencia.
Tenga en cuenta que no se dispone de un pico exacto de 0 dB. La normalización a cero dB utiliza los valores espectrales reales. Sin embargo, los picos mostrados están interpolados en banda y el pico de mayor potencia está ligeramente por encima de 0 dB.
Función de ventana
Seleccionar una función de ventana adecuada es todo un arte. En FlexPro hay veinte ventanas fijas y nueve ventanas cuyas propiedades pueden modificarse mediante un parámetro ajustable.
El ancho del lóbulo principal (mainlobe width), que aparece en la lista de selección como parámetro W, tiene una relación directa con la resolución de frecuencia. Una ventana con un ancho espectral de 3 solo tiene un tercio de la resolución en frecuencia de un espectro de Fourier no ponderado. El valor del lóbulo lateral, que también aparece en la lista de selección, es el valor en dB por el que el lóbulo lateral más grande está por debajo del lóbulo principal. Cuanto mayor sea este valor, mayor será la probabilidad de resolver un pico de baja potencia que se encuentre cerca de un componente de alta potencia. Otro factor que influye en la selección de las ventanas es el Rolloff. Cuanto mayor sea el Rolloff, mayor será la probabilidad de resolver un componente de baja potencia alejado del primer pico del espectro. El valor del lóbulo lateral (Sidelobe) es una medida del manchado espectral que se produce en su conjunto y el valor del Rolloff indica cómo se distribuye en el espectro.
El primer compromiso es la resolución frente al rango dinámico, que viene determinado por el ancho espectral (main lobe width). El segundo compromiso es la resolución de los picos vecinos en comparación con los picos muy separados. Se caracteriza por el valor del lóbulo lateral y el Rolloff.
La ventana Chebyshevproduce el pico más pronunciado del espectro para un valor de lóbulo lateral (Sidelobe) determinado. Se trata de una función de ventana adecuada para la resolución de componentes poco espaciados con distinta potencia. La ventana Coseno Maximum Rolloff produce la atenuación más rápida basada en el coseno en el dominio de la frecuencia, lo que permite analizar picos a muy baja potencia y a cierta distancia del primer pico. La ventana de Kaiser-Bessel es una ventana muy ajustable y, por tanto, constituye un muy buen compromiso entre los dos extremos.
La ventana Flattopes una característica especial. Aunque tiene un ancho del lóbulo principal de 5, es decir, ofrece una resolución espectral relativamente baja, el lóbulo principal tiene casi la misma magnitud en todo el rango desde una línea de frecuencia hasta sus vecinas izquierda y derecha. Por tanto, el lóbulo principal tiene un pico amplio pero plano. Esta ventana es, por tanto, especialmente adecuada para medir la potencia o las amplitudes de componentes de señales de banda estrecha, es decir, picos individuales en el espectro. La altura de un pico es casi independiente de su posición entre dos líneas de frecuencia debido a la forma especial del lóbulo principal.
Niveles de significación
FlexPro proporciona límites críticos basados en picos para determinar si un pico es estadísticamente significativo o no. La referencia es el ruido blanco (distribuido normalmente). Un límite crítico del 95 % es el nivel en el que solo en una de cada veinte señales individuales de ruido aleatorio, el pico más grande presente alcanzaría esta altura debido al principio de azar. Un límite crítico del 99,9 % es, en consecuencia, el nivel en el que el pico más grande alcanzaría esta altura para una sola de las mil señales individuales de ruido aleatorio.
Los límites críticos se basan en complejas pruebas de Monte Carlo, realizadas con los algoritmos y ajustes implementados. Se utilizan diferentes modelos para calcular el límite crítico para cada una de las funciones de ventana utilizadas en FlexPro. Para las ventanas ajustabls se utilizan modelos de superficie en 3D. Dado que este enfoque tiene en cuenta la caída de la altura del pico cuando se utilizan funciones de ventana, los límites críticos son correctos para todas las funciones de ventana, incluidas las que tienen parámetros ajustables.
Cambie el Límite crítico ruido blanco % a 99,9 %.
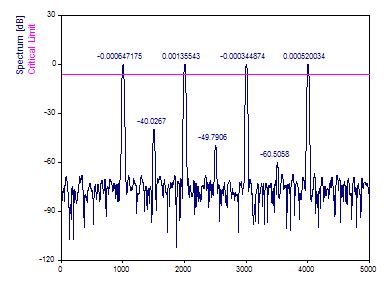
En este conjunto de datos, el mayor pico es significativo con un nivel de confianza superior al 99,9 %. Esta prueba solo compara el componente que tiene la mayor potencia con el ruido gaussiano. No se pueden extraer conclusiones sobre los demás picos.
Referencias
Este diagrama se conserva como referencia para comparaciones.
Para ello, pulse el botón Establecer referencia.
La referencia sustituye a la asignación del conjunto de datos. Tenga en cuenta que los límites críticos y los picos no se incluyen en las referencias.
Análisis espectral con baja varianza
A continuación, se presentan los procedimientos espectrales de FlexPro para los casos en los que se requiere una estimación espectral con baja varianza. Se asume que la precisión de la medición de la potencia tiene la máxima prioridad.
Reducción de la varianza de las medidas espectrales
La varianza de un FFT no disminuye si aumenta la longitud de los datos. En cambio, la varianza es una constante cuya raíz cuadrada (desviación típica) es aproximadamente igual a la potencia media de la señal. Para reducir la varianza de una estimación espectral basada en la FFT se utilizan técnicas de promediado y funciones de ventana ortogonales.
Periodograma (espectro de Fourier segmentado y solapado)
Existen dos procedimientos de Fourier en FlexPro para generar estimaciones del espectro con baja varianza. El primero de estos métodos es el "periodograma". Para una serie de datos estacionaria, cada sección debe tener las mismas propiedades espectrales. Por tanto, es posible sumar una serie de FFT para obtener una estimación espectral con una varianza reducida. Los FFT se calculan utilizando una ventana deslizante (un segmento de menor tamaño) que se desplaza por la serie de datos con un grado de solapamiento determinado. El FFT de menor tamaño da lugar a una resolución menor. Se sacrifica la resolución en favor de menores fluctuaciones en el resultado de la estimación espectral.
Seleccione la opción Periodograma para el procedimiento espectral. Siga utilizando el ajuste dB, normalizado como tipo de espectro. Seleccione la ventana Chebyshev y establezca el ancho de Fourier unilateral con Ajuste de la ventana en 4,0. Si es necesario, establezca la Longitud del segmento en el valor estándar longitud de datos/4, la Longitud de la FFT en 4096 y el Solapamiento en % en 90. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
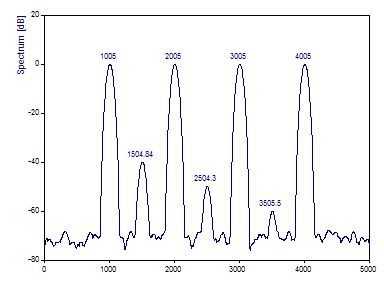
Haga clic en Etiquetado para visualizar las densidades de potencia espectral en dB.
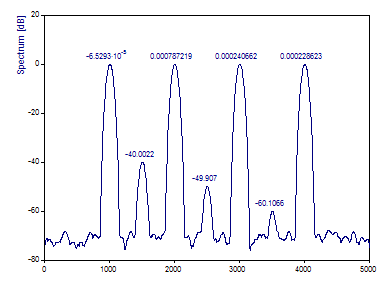
Con una longitud de segmento de 250 valores (1/4 de la longitud del conjunto de datos) y un solapamiento del 90 %, hay 31 segmentos discretos que, combinados, proporcionan un espectro con baja varianza. Como la longitud del segmento es solo una cuarta parte de la longitud total del conjunto de datos, la resolución en el dominio de frecuencias se reduce proporcionalmente. Por eso los picos del periodograma son más amplios. Pero hay 31 espectros de Fourier individuales que, sumados, producen el periodograma completo. Por este motivo, la potencia de los tres picos de baja potencia se registra con mayor precisión.
La ventana Chebyshev se ha utilizado aquí porque hay un ruido de fondo blanco constante distribuido en todas las frecuencias. Una ventana con un Rolloff elevado (rápido decaimiento de los lóbulos laterales) no tiene ventajas en este caso. Si hay ruido rojo (ruido que disminuye a frecuencias más altas), una ventana con un Rolloff alto, como Beta o Coseno Maximum Rolloff, sería una mejor opción.
La optimización del tamaño del segmento y del solapamiento no siempre es una tarea sencilla. En general, un gran número de segmentos no mejora significativamente la varianza. Normalmente, no se produce una reducción significativa de la varianza más allá de un solapamiento del 50 al 70 %, independientemente de que se utilicen o no funciones de ventana.
Amplitudes y funciones de ventana
Es un buen momento para observar los efectos de una función de ventana sobre la amplitud.
Cambie el Tipo de ventana a Rectángulo -13 dB W=1 (sin ventanas), la Normalización a Ninguna y cambie el Tipo de espectro a Amplitud.
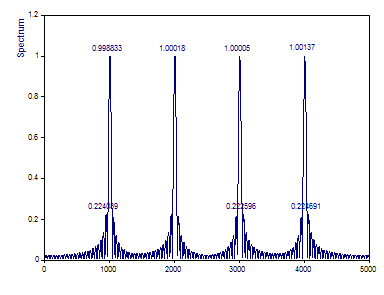
Tenga en cuenta que las amplitudes de las cuatro curvas senoidales de referencia, cada una de las cuales tiene una amplitud de 1, se reproducen con gran precisión debido al elevado solapamiento.
Cambie el Tipo de ventana a Cos2 Hamming -43 dB W=2.
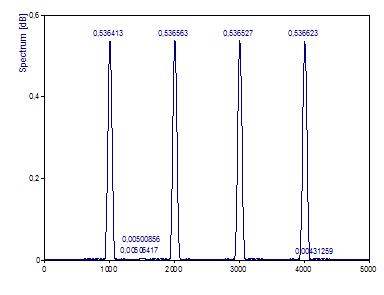
La ventana de Hamming es una ventana de coseno con una altura mínima del lóbulo lateral y un ancho unilateral del lóbulo principal de 2 líneas espectrales. Se puede ver que las amplitudes de los picos han disminuido aproximadamente un 50 %. Si el espectro consta de picos separados, esta reducción solo depende de la función de ventana seleccionada y, por tanto, puede compensarse fácilmente.
Cambie la Normalización a Amplitud.
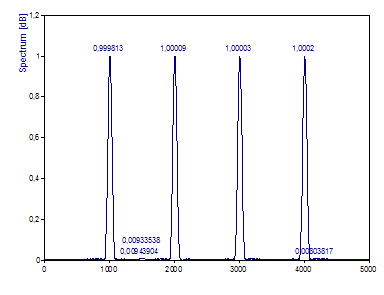
Las amplitudes de los picos corresponden ahora exactamente a las de las vibraciones de referencia de la señal. La normalización de la amplitud utiliza como factor de normalización la ganancia de la función de ventana seleccionada, es decir, la suma de los cuadrados de los valores de la función de ventana dividida por su número. Sin embargo, hay que tener en cuenta que este tipo de normalización no garantiza que la energía total del espectro sea igual a la de la señal de tiempo. Para los casos en que sea necesario, puede utilizar el tipo de normalización Potencia.
Optimización del periodograma
Cambie el Tipo de ventana a Cos3 Minimum Sidelobe -71 dB W=3.
El valor de atenuación de -71 dB de esta ventana debería dar como resultado un rango dinámico suficiente para detectar los tres picos de baja potencia.
Cambie el Tipo de espectro a dB, normalizado.
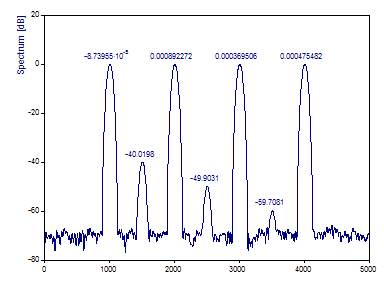
Puede ver que los tres componentes de banda estrecha con baja potencia se resuelven realmente cuando se utiliza esta función de ventana. Los picos también son más nítidos en esta ventana de ancho 3 que en la función de ventana Chebyshev de ancho 4, utilizada anteriormente. Aunque no se aplica a este ejemplo, hay casos en los que los componentes espectrales muy espaciados requieren una ventana cuyo valor de lóbulo lateral esté justo por debajo del ruido de fondo de los datos. Tenga en cuenta que las ventanas ajustables son continuas y, por lo tanto, es posible establecer cualquier ancho fraccional de Fourier deseado.
Cambie el Tipo de ventana a Chebyshev y establezca el Ajuste de la ventana del ancho de Fourier unilateral en 2,9.
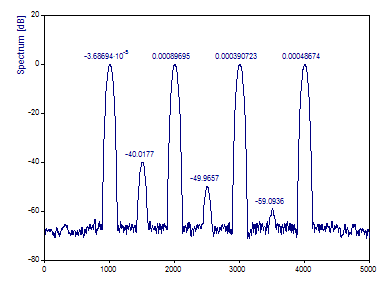
La figura muestra una ventana casi óptima para minimizar el ancho de los picos. Los picos tienen el ancho mínimo para poder detectar componentes de baja potencia frente al ruido de fondo. Sin embargo, esta no es necesariamente la configuración óptima para el periodograma. Si se sacrifica un poco de la varianza mejorada, es posible obtener un espectro más nítido.
Seleccione 500 en el cuadro de lista de Longitud de segmento y mantenga el valor 90 para el Solapamiento en %.
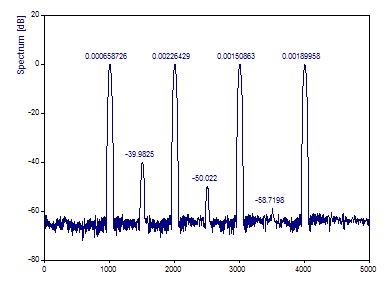
Si se utilizan estos ajustes, se emplean 11 espectros de Fourier de longitud media para generar el periodograma. Tenga en cuenta que los picos son ahora mucho más nítidos. La mayor varianza en la zona ruidosa del espectro es tan evidente como la representación muy imprecisa de los componentes de baja potencia.
Análisis espectral multitaper
El segundo método en FlexPro para generar espectros de baja varianza es el procedimiento multitaper. En un procedimiento multitaper, se aplica a los datos un conjunto de funciones de ventana ortogonales y los espectros se promedian de una determinada manera para obtener un espectro compuesto. A diferencia del procedimiento de solpamaiento de segmentos, que solo utiliza una parte del conjunto de datos para cada espectro individual, el procedimiento multitaper utiliza todo el conjunto de datos con cada función de ventana.
Un procedimiento multitaper es algo similar a promediar los espectros de un gran número de funciones de ventana. En este caso, sin duda habría una una redundancia, ya que las distintas funciones de ventana están fuertemente correlacionadas entre sí (todas tienen formas de pico similares). Sin embargo, las funciones de ventana ortogonales utilizadas en el espectro multitaper no están correlacionadas, a diferencia de las funciones de ventana convencionales. Solo la primera función de ventana tiene la forma conocida.
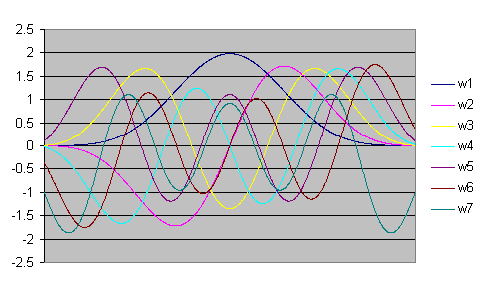
Los espectros de las distintas funciones de ventana no generan un pico central común para un componente armónico. Solo la primera función de ventana produce un pico central en la frecuencia armónica del componente. Las demás funciones de ventana generan picos cuya frecuencia se desvía ligeramente hacia arriba o hacia abajo. Cada uno de los espectros contribuye con su parte al espectro global.
Las ventajas del análisis multitaper son que no se sacrifica resolución ni se pierde información en los bordes del conjunto de datos. Si bien es cierto que hay una pérdida de información en los bordes de la primera función de ventana, los datos correspondientes están contenidos y resaltados en las ventanas siguientes. La forma de los picos espectrales asignados a los distintos componentes facilita la determinación de la potencia relativa. El inconveniente es que la envolvente espectral asociada a cada componente no proporciona una resolución de frecuencia nítida.
El procedimiento mutlitaper siempre realiza una normalización de potencia para el espectro resultante. Por lo tanto, las selecciones Ninguno y Potencia en la lista Normalización conducen al mismo resultado. Sin embargo, al igual que con el periodograma, el tipo de normalización Amplitud puede utilizarse para compensar la atenuación de amplitud de los picos en el espectro. Los factores de normalización se determinaron empíricamente en función del número de ventanas y de su ancho.
Seleccione Espectro multitaper como Procedimiento espectral y seleccione el Tipo de espectro dB, normalizado. Establezca el ancho de Fourier unilateral (ajuste de la ventana) en 3,0. En Número de ventanas DPSS introduzca el valor máximo o 5. Establezca la Longitud de la FFT en 4096. Haga clic en el Etiquetado hasta que las frecuencias aparezcan sobre los picos.
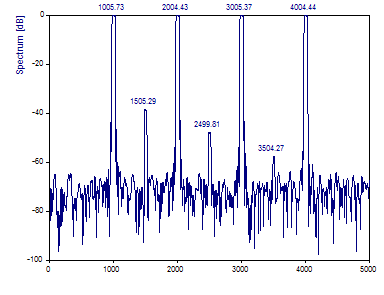
Tenga en cuenta la forma aplanada de los picos. La forma de los picos facilita el reconocimiento de la potencia espectral relativa, pero dificulta la localización de la frecuencia central de la envolvente del pico. FlexPro utiliza las posiciones de pico en el espectro del valor F para determinar las frecuencias de pico. Los valores F son una medida de significación y no tienen relación directa con la varianza.
Haga clic en el botón de Etiquetado para visualizar la densidad espectral en dB.
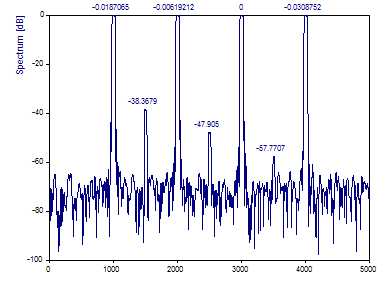
Como puede ver, promediar los espectros de las funciones de ventana ortogonales no lleva a un ruido de fondo más alisado, a diferencia del periodograma.
Como la envolvente multitaper no tiene picos claramente definidos, no se puede determinar con exactitud el máximo del espectro. Esta es una posible razón por la que los tres picos de baja potencia se desvían en +2 dB en el espectro normalizado.
Una nota importante para el análisis espectral multitaper se refiere al número de funciones de ventana que deben utilizarse. Para un análisis de Fourier unilateral con un ancho de 3,0, FlexPro admite hasta 5 funciones de ventana. Se pueden utilizar hasta 7 funciones de ventana DPSS para un ancho de 4,0. El rango dinámico de las funciones de ventana DPSS individuales disminuye a medida que avanza la secuencia. La primera función de ventana DPSS, w1 en la figura, es una función de ventana excelente y ofrece el mejor rango dinámico de la secuencia (es la ventana Slepianajustable del procedimiento de análisis de Fourier y periodograma). Cada ventana posterior de la secuencia DPSS ofrece un rango dinámico reducido. Si se requiere un amplio rango dinámico, a menudo es mejor excluir la última ventana o las dos últimas ventanas de la secuencia. Por ejemplo, para un ancho de Fourier de 3, un número total de funciones de ventana de 3 o 4 es la mejor opción. Para un espectro con un ancho de Fourier de 4, 5 ventanas proporcionarían el mejor resultado.
Cambie el Número de ventanas DPSS a 3.
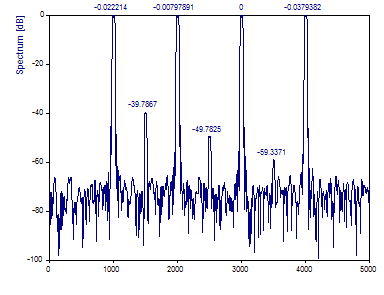
Puede observar que los picos son cada vez más precisos.
Atenuación de la amplitud en el espectro multitaper
Cambie el Número de ventanas DPSS a 5 o máximo, la Normalización a Potencia y cambie el Tipo de espectro a Amplitud.
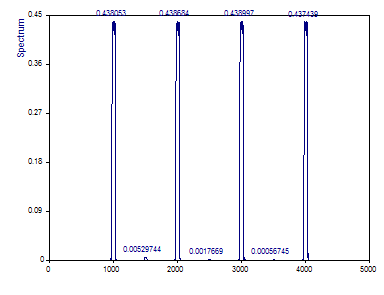
Para un periodograma con una función de ventana de Fourier de ancho 3, la atenuación de la amplitud es de aproximadamente el 24 % (se muestra el 76 % de la amplitud real). Para un espectro multitaper con una ancho de Fourier de 3, la atenuación es considerablemente mayor: un 56 % (solo se muestra el 44 % de la amplitud).
Cambie el Número de ventanas DPSS a 3.
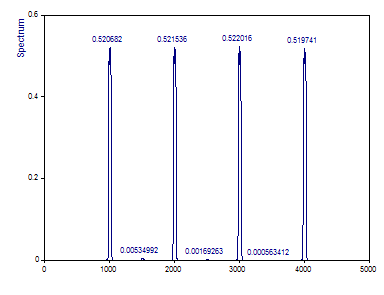
La atenuación no solo depende del ancho de Fourier del análisis multitaper, sino que también influye decisivamente el número de funciones de ventana utilizadas. En el caso de que solo se utilicen las tres primeras funciones de ventana de Slepian, la atenuación de la amplitud es aproximadamente del 48 %, frente al 56 % de atenuación con el número máximo de 5 funciones de ventana.
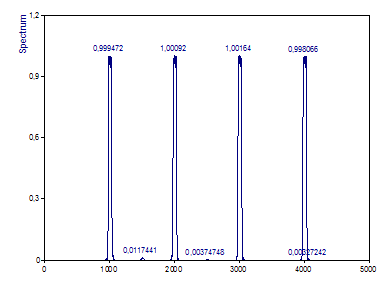
Seleccionando el tipo de normalización Amplitud se compensa perfectamente la atenuación.
El mejor método para un análisis de Fourier con alto rango dinámico y baja varianza
(1) Asegúrese de que los datos son estacionarios en sentido amplio (WSS = Wide-Sense Stationary) a lo largo de toda la longitud de los conjuntos de datos. Utilice el análisis STFTo CWT para garantizar que el contenido espectral del conjunto de datos no depende del tiempo. Una función de ventana reducirá significativamente la información en ambos finales del conjunto de datos. Esto solo debe hacerse si se puede ignorar con seguridad la influencia de los datos en los dos bordes del conjunto de datos.
(2) Para reducir el manchado espectral y lograr un análisis de Fourier con un alto rango dinámico, suelen ser necesarias las funciones de ventana. Tenga en cuenta, por tanto, que las amplitudes y potencias del espectro están atenuadas y, por ello, no pueden leerse directamente de los picos. Para evaluar la potencia y las amplitudes con precisión, utilice la normalización de amplitud.
(3) Si la longitud de los datos es muy grande, el análisis comienza con una alta resolución en el dominio de la frecuencia. Se puede sacrificar parte de ello para reducir la varianza utilizando el método del periodograma.
(4) Si la longitud de los datos es limitada y el objetivo del análisis es estimar tanto la frecuencia como la potencia, puede ser necesario utilizar el espectro de Fourier único. Aunque los picos del espectro tienen la máxima resolución posible, la varianza es mayor porque hay más picos causados por el ruido. El análisis espectral de Fourier es también la mejor forma de distinguir una señal determinada del ruido, ya que ofrece límites críticos para todas las funciones de ventana, mientras que con el periodograma solo pueden visualizarse en el caso no ponderado.
(5) Cuando la longitud de los datos es limitada y el objetivo principal del análisis es estimar la potencia, especialmente cuando toda la información de los datos es importante, sobre todo la de los bordes del conjunto de datos, el espectro multitaper es la mejor opción.
(6) Los tres métodos de análisis son aplicables a diversos problemas de análisis espectral. FlexPro facilita la selección del método adecuado al ofrecer los tres algoritmos en una única opción de análisis. Los distintos procedimientos pueden compararse utilizando la función de referencia. A veces, el mejor resultado del análisis se consigue utilizando los tres métodos.
Paso 3 - Opciones de salida
Para visualizar los objetos generados automáticamente por el asistente para análisis, genere un espectro de Fourier.
Seleccione el Espectro de Fourier como Procedimiento espectral. Seleccione dB, normalizado como Tipo de espectro. Seleccione Kaiser-Bessel como Tipo de ventana e introduzca 3,0 como Ajuste de la ventana. Establezca la Longitud de la FFT en 8192. Seleccione la opción Número máximo de picos e introduzca un valor de 7. Ahora establezca el Límite crítico de ruido blanco % en 99. Haga clic en el botón Etiquetado hasta que aparezcan el etiquetado de frecuencia en el gráfico. Haga clic en Siguiente. En el paso 3, marque las tres opciones y haga clic en Finalizar.
Se crearon ocho objetos en la base de datos del proyecto de FlexPro.
"Espectro" es el objeto de análisis. Realiza el análisis espectral. Puede abrir el objeto haciendo doble clic sobre él.
"Límite crítico" es la fórmula para generar los límites críticos utilizados en la visualización.
"Picos" es la fórmula para generar la información de los picos utilizada en la pantalla.
"Análisis armónico" es la fórmula que genera el informe de análisis armónico.
El diagrama "Espectro" es la representación del espectro de Fourier generado por el asistente para análisis. Utilice los objetos "Espectro", "Límite crítico" y "Picos".
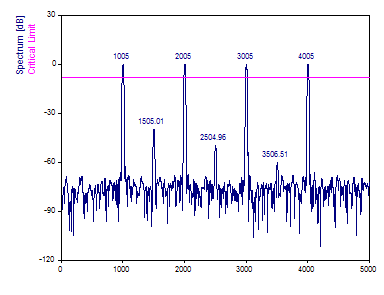
"Datos" es un diagrama de los datos originales del domino del tiempo.
"Análisis armónico" es una tabla con la información espectral de los siete componentes espectrales, definidos por el número máximo de picos de 7. Esta tabla muestra la frecuencia, la amplitud, la fase y la potencia TISA. En "% de potencia", la suma de todos los componentes proporciona el 100 %; los valores de la columna "Relativo %" asignan el 100 % al componente de mayor potencia.
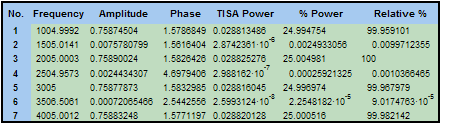
"Fourier" es un documento que contiene los espectros y diagramas de los datos.
Análisis espectral de datos muestreados de forma no equidistante
La siguiente sección describe las posibilidades del análisis espectral de Fourier de datos muestreados de forma no equidistante en FlexPro. La atención se centra en un procedimiento de Fourier diseñado para datos de muestreo desigual.
Puede saltarse el resto de este tutorial si siempre trabaja con valores muestreados uniformemente.
Abra la carpeta Tutorials en la base de datos de ejemplo y la subcarpeta Fourier Uneven y haga doble clic en Data para abrir el diagrama 2D.
Aquí puede ver la representación de la señal con 1000 valores en coma flotante. Los valores X están en orden ascendente en el rango de 0 a 10, pero no tienen un intervalo de muestreo constante. Este es el "peor escenario" para el algoritmo de Fourier aplicado a datos muestreados de forma no equidistante.
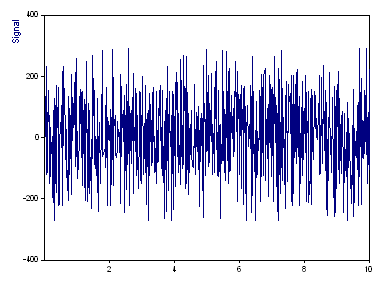
Este conjunto de datos contiene tres picos, uno a frecuencia 30 (amplitud 100, fase 3π/2), otro a frecuencia 70 (amplitud 100, fase π) y un tercer pico a frecuencia 120 (amplitud 100, fase π/2). La frecuencia media de Nyquist resultante del valor recíproco de la frecuencia media de muestreo es 50,05. Por tanto, hay dos picos por encima de este límite.
Una diferencia importante entre los datos muestreados irregularmente y los datos muestreados uniformemente es el hecho de que la información por encima del límite medio de Nyquist ya no se refleja ("aliased") automáticamente a frecuencias más bajas. Por tanto, es posible extraer información que se encuentra por encima de la frecuencia de Nyquist, ya que algunos de los valores de los datos están más próximos entre sí y, por tanto, tienen una frecuencia de Nyquist "local" mucho mayor.
Por consiguiente, hay puntos más alejados cuya frecuencia local de Nyquist es inferior a la media. Por lo tanto, la información dentro del rango medio de Nyquist es incompleta.
Periograma de Lomb-Scargle
El periodograma de Lomb-Scargle es un algoritmo que genera un espectro de Fourier específico para el caso en que los datos están desigualmente distribuidos.
Cierre el diagrama y seleccione el conjunto de datos Signal.
Haga clic en Insertar[Análisis] > Asistente para análisis. Seleccione Análisis para datos muestreados de forma no equidistante en Análisis espectral y, a continuación, Espectro de Fourier, no equidistante. Haga clic en Siguiente.
En el paso 2 del asistente para análisis, se comienza visualizando el espectro de Fourier no ponderado con una frecuencia máxima que corresponde a la frecuencia media de Nyquist.
Seleccione dB, normalizado como Tipo de espectro. Seleccione Rectángulo -13 dB W=1 (sin ventana) como Tipo de ventana. Establezca el número de frecuencias en 1024 y el múltiplo de Nyquist en 1,0. Active el Número máximo de picos e introduzca 3. Límite crítico de ruido blanco % se establece en 99.
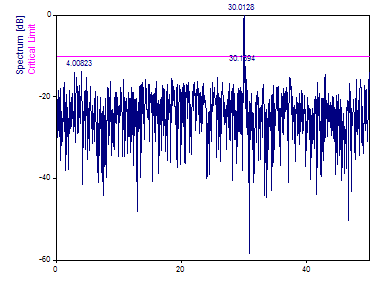
Solo se encontró un pico a frecuencia 30, ya que los picos a frecuencia 70 y 120 están por encima de la frecuencia media de Nyquist.
El pico más grande está por encima del límite crítico del 99 %, lo que significa que hay menos de un uno por ciento de probabilidad de que este componente espectral más grande haya sido causado por ruido. En otras palabras, con 100 conjuntos de datos de ruido blanco con la misma varianza, no se esperaría que ninguno tuviera un pico de este valor absoluto.
Tenga en cuenta también que este algoritmo no genera una línea espectral para la frecuencia 0.
Ampliar el espectro más allá de la frecuencia media de Nyquist
Cambie el Múltiplo de Nyquist a 2,0. Para mantener la densidad espectral, aumente el Número de frecuencias a 2048.
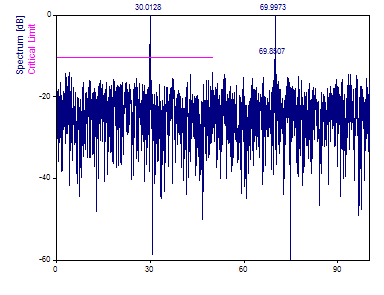
Puede ver que los componentes de frecuencia 30 y 70 son visibles en el espectro.
Cambie el Múltiplo de Nyquist a 4,0. Para mantener la densidad espectral, aumente el Número de frecuencias a 4096.
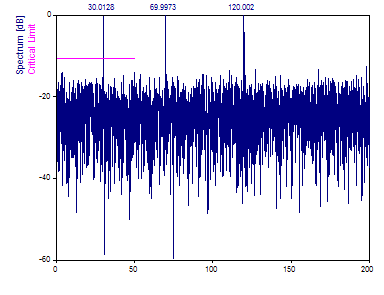
Si amplía el espectro hasta cuatro veces el límite medio de Nyquist, se detectarán todos los componentes, incluido el pico a frecuencia 120.
Tenga en cuenta que este algoritmo utiliza una interpolación interna que no está exenta de errores. Las curvas senoidales de los datos se crean sin ruido y, sin embargo, se muestra un ruido de fondo de aproximadamente -25 dB. Esto limita las posibilidades de aplicación de este procedimiento para un análisis de Fourier con un alto rango dinámico.
Función de ventana
FlexPro amplía el algoritmo para ofrecer ventanas. Se ofrecen todas las ventanas que pueden aplicarse a valores de tiempo distribuidos de forma desigual. Las ventanas Chebyshev y Slepian (DPSS) no están disponibles, aunque se dispone de una ventana Chebyshev aproximada para determinar el pico más pronunciado posible para un lóbulo lateral mayor determinado.
Cambie el Tipo de ventana a Cos3 Minimum Sidelobe -71 dB W=3.
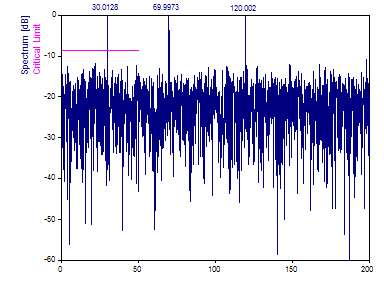
Debido al error de interpolación, la función de ventana aporta pocas mejoras.
Límites críticos
El periodograma de Lomb-Scargle suele contener un límite de confianza basado en la distribución exponencial. Esto no se utiliza en FlexPro. En su lugar, se dispone de límites críticos. Al igual que en el análisis de Fourier para datos muestreados de forma equidistante, aquí también se utilizan modelos especiales para calcular los límites críticos de cada una de las funciones de ventana ofrecidas. Se basan en elaboradas complejas pruebas de Monte Carlo. Dado que la distribución de los valores de la abscisa puede influir en los límites críticos, los límites críticos mostrados deben considerarse una aproximación.
Atenuación de amplitud
Cambie el Tipo de ventana a Rectángulo -13 dB W=1, la Normalización a Potencia y establezca el campo Múltiplo de Nyquist en 3. Seleccione Amplitud como Tipo de espectro.
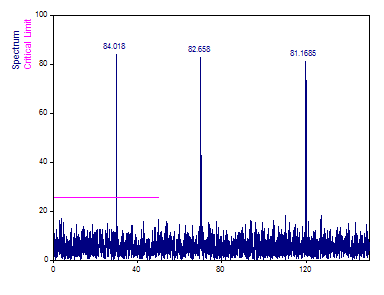
A diferencia del análisis de Fourier para datos muestreados de forma equidistante, donde desactivar la ventana permite mostrar valores casi iguales a los de amplitud real, el algoritmo de Lomb-Scargle también da lugar en este caso a una atenuación si se desea conservar la energía de la señal en el espectro. El uso de funciones de ventana conduce a una mayor atenuación de la amplitud y la potencia.
La elección de la amplitud de normalización compensa la atenuación.
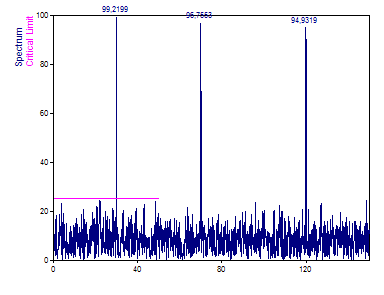
Haga clic en Siguiente. En el paso 3, marque las tres opciones y haga clic en Finalizar.
A su vez, se crearon ocho objetos en la base de datos del proyecto de FlexPro. La única diferencia es que no se ha calculado la fase de los componentes espectrales, ya que esto no es posible con este algoritmo.
Bibliografía
Buenas introducciones al procesamiento digital de señales son:
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.
•H.D. Lüke (1985). Transmisión de señales. Springer-Verlag Berlin, Heidelberg, New York. ISBN 3-540-15526-0.
Los algoritmos FFT utilizados en FlexPro se describen aquí:
•C. Temperton, "Implementation of a Self-Sorting In-Place Prime Factor FFT Algorithm", Journal of Computational Physics, v. 58, p. 283, 1985
•R. C. Singleton, "An Algorithm for Computing the Mixed Radix Fast Fourier Transform", IEEE Trans. Audio Electroacoust., v. AU-17, p. 93, junio 1969
•L. R. Rabiner, R. W. Schafer, C. M. Rader, "The Chirp z-Transform Algorithm and Its Application", BSTJ, 48, pág. 1249, mayo-junio de 1969
Encontrará información sobre las funciones de ventana en:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, feb. 1981.
Aquí encontrará información sobre los espectros multitaper:
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, pág. 199, 1995.