Calcula la transformada de Hilbert. Suele utilizarse para calcular la amplitud instantánea o la frecuencia instantánea y para la demodulación de señales.
Sintaxis
Hilbert(Signal [ , FFTLength = 0 ])
La sintaxis de la función Hilbert consta de los siguientes elementos:
Parte |
Descripción |
|---|---|
Signal |
El conjunto de datos real a partir de los cuales debe calcularse la señal analítica. El conjunto de datos debe estar muestreado de forma equidistante, ya que el algoritmo utiliza la transformada discreta de Fourier (para datos equidistantes). Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos excepto Tiempo de calendario y Intervalo de tiempo. No se permiten valores inválidos en este argumento. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
FFTLength |
La longitud de la transformada de Fourier necesaria para calcular la transformada de Hilbert. La longitud de la FFT debe ser mayor o igual que la longitud de los datos. Si la longitud de la FFT especificada es mayor que la longitud de los datos, se añaden ceros para la transformada de Fourier interna. Un valor de -1 establece la longitud de la FFT a la siguiente potencia de 2 mayor. El valor predeterminado 0 ajusta la longitud de la FFT a la longitud de los datos. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que -1. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 0 si no se especifica el argumento. |
Notas
El resultado tiene la misma estructura y unidad que el argumento Signal.
En el caso de las estructuras de datos compuestas, solo se calcula el componente Y. Los componentes X y Z, si existen, se transfieren sin cambios al resultado. Para matrices de datos y series de señales, el cálculo se realiza columna por columna.
La transformada de Hilbert se define mediante una transformación integral lineal para una señal (real o de valores complejos) x(t) de la siguiente manera:
Con esta definición, la transformada de Hilbert también puede escribirse de forma equivalente como una convolución:
Aplicando la transformada de Fourier a la última ecuación, la función de transferencia H de la transformada de Hilbert se calcula del siguiente modo:
En otras palabras: La transformada de Hilbert puede interpretarse como un desplazamiento de fase de -π/2 (es decir, -90 grados) para frecuencias positivas y de π/2 (es decir, 90 grados) para frecuencias negativas. Por ejemplo, la transformada de Hilbert de la función coseno da como resultado la función seno.
Como referencia, véase [1] y [4].
Aplicación: Amplitud instantánea, fase instantánea, frecuencia instantánea, envolvente y demodulación de señales
La transformada de Hilbert se utiliza a menudo para calcular cantidades instantáneas de la señal original: laamplitud instantánea (instantaneous amplitude), fase instantánea (instantaneous phase) y frecuencia instantánea (instantaneous frequency). La amplitud instantánea también proporciona la envolvente superior de la señal que se va a analizar.
Estas variables instantáneas también pueden utilizarse para demodular señales (demodulación de amplitud, demodulación de fase y demodulación de frecuencia).
Sin embargo, los cálculos se refieren a la señal analítica derivada de la transformada de Hilbert y no directamente a la transformada de Hilbert.
Puede consultar más detalles, definiciones y ejemplos en la ayuda en línea de la función AnalyticSignal o del objeto de análisis Magnitud instantánea.
Antecedentes teóricos: Algoritmo para el cálculo de la transformada de Hilbert
La regla de cálculo continua en el tiempo indicada anteriormente define la función de transferencia en el dominio de la frecuencia. El algoritmo para calcular la transformada discreta de Hilbert se realiza, por tanto, con ayuda de la FFT y la función de transferencia discreta H, de forma análoga al algoritmo de la función AnalyticSignal (véase también [1]):
La única diferencia radica en la definición de la función de transferencia.
Esto se expresa para longitudes de la FFT pares como: H[k] = -i para k = 1, 2..., FFTLength/2 - 1 (corresponde a las frecuencias positivas) y H[k] = i para k = FFTLength/2 + 1..., FFTLength (corresponde a las frecuencias negativas). i denota aquí la unidad imaginaria. Los coeficientes simétricos k = 0 y k = FFTLength/2 tienen una posición especial. Para ellos, H[k] = 0.
Para longitudes de la FFT impares, la función de transferencia se expresa análogamente como: H[k] = -i para k = 1, 2..., (FFTLength-1)/2 y H[k] = i para k = (FFTLength-1)/2 + 1..., FFTLength y también H[0] = 0.
El algoritmo FPScript para calcular la transformada discreta de Hilbert corresponde, por tanto, al algoritmo FPScript de la función AnalyticSignal, con la excepción de la definición de la función de transferencia. El código análogo se encuentra en la ayuda en línea de la función AnalyticSignal.
Influencia de la longitud de la FFT: La resolución de la FFT necesario para el algoritmo aumenta mediante el relleno de ceros, es decir, seleccionando una longitud de la FFT mayor que la longitud de los datos. Esto puede mejorar el resultado del cálculo. El siguiente ejemplo lo ilustra.
La función de transferencia de esta transformación corresponde a la transformación de la definición de la función AnalyticSignal. Por tanto, la transformada de Hilbert puede definirse de forma equivalente como la parte imaginaria de la señal analítica asociada a la señal x(t).
Disponibilidad
Opción Análisis espectral
Ejemplos
Imag(AnalyticSignal(realSig))
Devuelve la transformada de Hilbert de una señal real. El código es equivalente a Hilbert(realSig).
realSig + 1i * Hilbert(realSig)
Transforma una señal real en una señal analítica cuya parte imaginaria corresponde a la transformada de Hilbert. El código es equivalente a AnalyticSignal(realSig).
Dim t = Series(0, 10, 0.005)
Hilbert(Signal(Cos(t), t))
Calcula la transformada de Hilbert de la función coseno. El resultado es la función seno.
Dim t = Series(-25, 25, 0.005)
Dim sig = Signal(Sinc(t), t)
Dim hilbTrafo = Hilbert(sig, NumberOfRows(sig))
List("Hilbert Trafo calculated", hilbTrafo, "Hilbert Trafo exact", Signal((1-Cos(t))/t, t))
Calcula la transformada de Hilbert de la función Sinc. También se obtiene el resultado exacto, que viene dado por la función 1/t - Cos(t)/t. La comparación en un diagrama 2D proporciona:
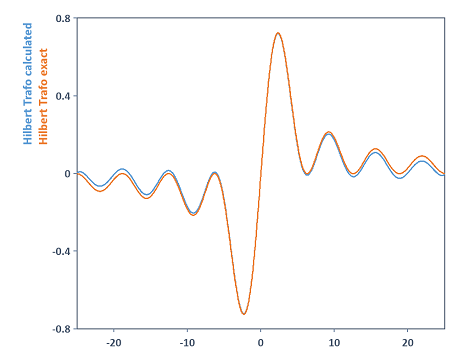
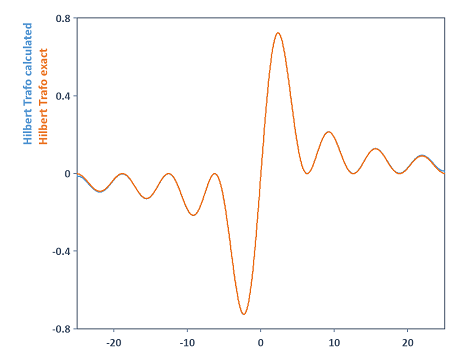
En este ejemplo, si se aumenta la longitud de la FFT al calcular la variable hilbTrafo al valor 131072, por ejemplo, se obtiene un resultado de cálculo más preciso para la transformada de Hilbert. Ahora ambas curvas son casi idénticas:
Véase también
Objeto de análisis Magnitud instantánea
Bibliografía
[1] S. Lawrence Marple, Jr.: Computing the Discrete-Time "Analytic" Signal via FFT. En: IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222, 1999.
[2] B. Boashash: Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals. En: Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono: On Instantaneous Amplitude and Phase of Signals. En: IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833, 1997.
[4] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck: Discrete-Time Signal Processing, 2nd Ed.. Upper Saddle River, NJ: Prentice Hall, 1999.