Calcula la función de Bessel de primera especie con el orden especificado.
Sintaxis
Jn(n, Number)
La sintaxis de la función Jn consta de los siguientes elementos:
Parte |
Descripción |
|---|---|
n |
El orden. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 0. |
Number |
El argumento para la función. Todas las estructuras de datos están permitidas. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. |
Notas
El tipo de datos del resultado es siempre En coma flotante de 64 bits.
La estructura del resultado corresponde a la del argumento Number, si es necesario, el cálculo se realiza elemento por elemento.
El resultado tiene la unidad 1, siempre y cuando Number tenga una unidad; en caso contrario, no tiene ninguna unidad.
En el caso de las estructuras de datos compuestas, solo se calcula el componente Y.
La función real de Bessel se calcula para un argumento real. El resultado tiene entonces el tipo de datos número en coma flotante de 64 bits. El siguiente gráfico muestra el curso de la función para los órdenes 0 a 4 en el intervalo [-40, 40]:
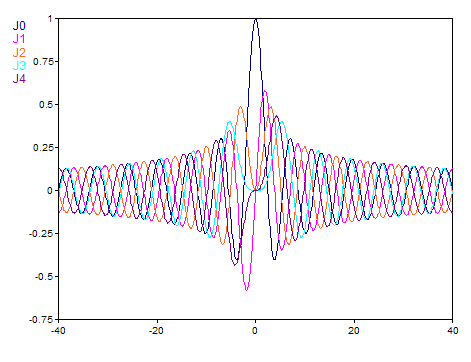
Si Number es compleja, se calcula la función compleja de Bessel. El resultado tiene entonces el tipo de datos número complejo en coma flotante de 64 bits. El siguiente gráfico muestra el curso del valor absoluto de la función para orden 2:
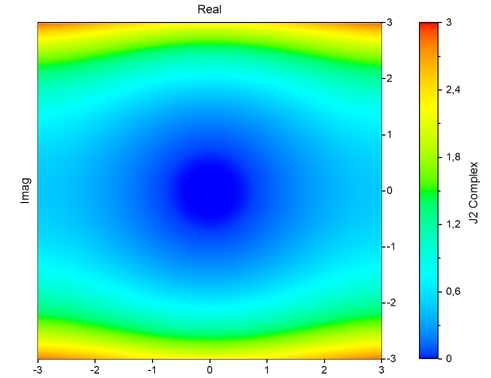
Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista.
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
Jn(2, 0) |
Devuelve 0. |
Dim x |
Calcula una lista de tres señales con la evolución de las funciones de órdenes 0, 1 y 2 en el intervalo [-40, 40]. |
Véase también
Bibliografía
[1] Donald E. Amos: AMOS - A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order. En: www.netlib.org. https://netlib.org/amos/, 1986.