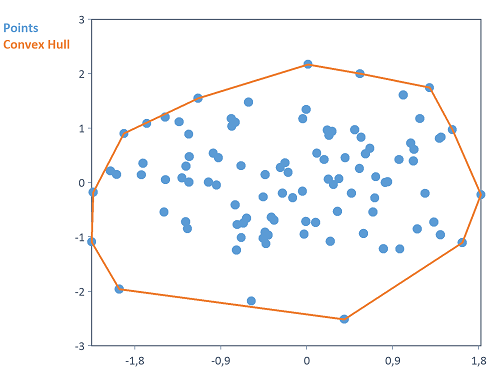
Calcula la envolvente convexa de un conjunto de puntos bidimensional.
Sintaxis
ConvexHull(Points [ , Algorithm = CONVEXHULL_GRAHAM_SCAN ])
o
ConvexHull(Y, X [ , Algorithm = CONVEXHULL_GRAHAM_SCAN ])
La sintaxis de la función ConvexHull consta de los siguientes elementos:
Parte |
Descripción |
||||||
|---|---|---|---|---|---|---|---|
Points |
El conjunto de puntos Y y X para los que debe calcularse la envolvente convexa. Las estructuras de datos permitidas son Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||
Y |
El conjunto de puntos Y utilizado para calcular la envolvente convexa. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||
X |
El conjunto de puntos X utilizados para calcular la envolvente convexa. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||
Algorithm |
Determina el algoritmo para calcular la envolvente convexa. El argumento Algorithm puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado CONVEXHULL_GRAHAM_SCAN si no se especifica el argumento. |
Notas
El resultado siempre tiene la estructura de datos Señal.
Los valores se convierten en números en coma flotante de 64 bits antes del cálculo.
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
Dim y = Noise(1# 100, NOISE_NORMAL, 0)
Dim x = Noise(1# 100, NOISE_NORMAL, 0)
Dim points = Signal(y, x)
List("Points", points, "Convex Hull", ConvexHull(points))
Calcula la envolvente convexa de puntos distribuidos aleatoriamente en el plano bidimensional.