Puede utilizar este objeto de análisis para realizar una aproximación circular, es decir, un ajuste de curva circular a los datos subyacentes. Utilice la aproximación circular para el análisis de las mediciones de redondez y la evalución de las vibraciones del eje (véase [1], [2] [4]). Están disponibles los procedimientos de aproximación circular LSCI, MCCI, MICI, MZCI y un procedimiento elemental de aproximación circular (análogo a la norma ISO 7919-1 de [3]).
También puede eliminar los valores atípicos circulares de los datos y aplicar un filtro de Gauss para aplicar el alisado antes de realizar la aproximación circular. Los datos subyacentes también se denominan a continuación perfil.
Descripción y resultados de salida
Los procedimientos de aproximación circular LSCI, MCCI, MICI y MZCI calculan uno o varios círculos de referencia, que se determinan de forma diferente en función del procedimiento seleccionado:
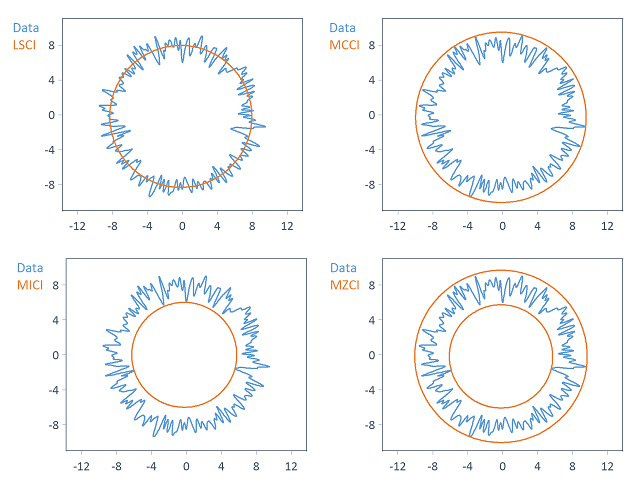
Nota Dependiendo del procedimiento de aproximación circular seleccionado, las coordenadas del centro del círculo de los círculos de referencia pueden diferir en mayor o menor medida.
El círculo interior, el círculo central y el círculo exterior se derivan y calculan a partir del círculo de referencia (o círculos) de referencia (cada uno con el mismo centro del círculo que el círculo de referencia). El objeto de análisis puede devolver como resultados los círculos, los parámetros estadísticos (por ejemplo, los radios de los círculos y las coordenadas de los centros de los círculos) y los datos prefiltrados. Puede especificar el Número de valores de los círculos como parámetro.
En todos los casos, la redondez está disponible como parámetro estadístico (también conocido como desviación de redondez). Siempre se calcula como la diferencia entre el radio del círculo exterior y el radio del círculo interior (y, por tanto, se deriva del círculo de referencia respectivo). La desviación de redondez es una medida para la redondez del perfil medido. Para el procedimiento LSCI y el procedimiento de aproximación circular elemental (determinación del centro del círculo mediante el cálculo del valor medio de la trayectoria circular), se calculan y emiten otros valores característicos estadísticos como se describe a continuación.
En la siguiente imagen muestra los círculos generados y los parámetros estadísticos para el ejemplo del procedimiento de aproximación circular LSCI:
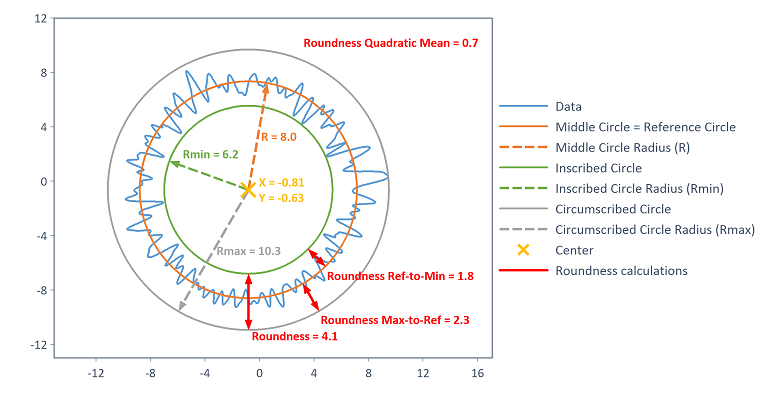
LSCI - Círculo de referencia de mínimos cuadrados (Least Squares Circle)
El cálculo del círculo de referencia de mínimos cuadrados LSCIse basa en la función LeastSquaresCircle. El círculo LSCI se calcula como el círculo en el que se minimiza la suma de los cuadrados de las desviaciones con respecto a los datos. En la bibliografía también se denomina como círculo de Gauss. El círculo interior se obtiene como el mayor círculo interno en relación con el centro del círculo LSCI. El círculo exterior se obtiene como el círculo más pequeño en relación con el centro del círculo LSCI. El círculo central se corresponde con el círculo de referencia, es decir, el círculo LSCI.
Existen los dos algoritmos siguientes para calcular el círculo LSCI:
Algoritmo |
Descripción |
|---|---|
Kasa |
El algoritmo Kasa es sencillo, rápido y robusto. Ofrece buenos resultados si los puntos de datos se han muestreado a lo largo de un círculo completo o de una gran parte de él (al menos un semicírculo). |
Pratt |
El algoritmo Pratt es ligeramente más lento que el método de Kasa, pero igual de preciso y rápido. En comparación con el método Kasa, se obtienen mejores resultados si los puntos de datos solo están disponibles dentro de un pequeño arco circular. |
Como parámetros estadísticos, el procedimiento LSCI proporciona, además de la desviación de redondez, la desviación de redondez de pico a referencia (diferencia entre el radio del círculo exterior y el radio del círculo de referencia), la desviación de redondez de referencia a valle (diferencia entre el radio del círculo de referencia y el radio del círculo interior) y el valor medio cuadrático de las desviaciones de los puntos de datos respecto al círculo de referencia (según [1]).
MCCI - Círculo de referencia mínimo circunscrito (Minimum Circumscribed Circle)
El cálculo del círculo de referencia MCCIse basa en la función MinimumCircumscribedCircle. En este procedimiento, el círculo de referencia se calcula como el círculo con el diámetro más pequeño posible que puede situarse en el perfil desde el exterior. También se conoce como círculo envolvente. Por lo tanto, el círculo exterior se corresponde con el círculo de referencia en este procedimiento. El círculo interior se obtiene como el mayor círculo interior en relación con el centro del círculo de referencia. El círculo central también se define aquí como el círculo promediado aritméticamente entre el círculo de referencia (es decir, el círculo exterior) y el círculo interior.
Para calcular el círculo MCCI, el algoritmo subyacente requiere del cálculo del casco convexo. La envolvente convexa puede calcularse utilizando uno de los dos procedimientos que se indican a continuación:
Algoritmo |
Descripción |
|---|---|
Jarvis-March |
El tiempo de ejecución del algoritmo es O(n*h), siendo h el número de puntos del casco convexo y n el número de valores de los datos de entrada. En el peor de los casos, el algoritmo tiene un tiempo de ejecución cuadrático. Sin embargo, en muchas aplicaciones el número de puntos del casco convexo es pequeño, por lo que el algoritmo es más rápido que el algoritmo de Graham-Scan en estos casos. |
Graham-Scan |
El tiempo de ejecución del algoritmo es siempre O(n*log(n)). En general, el algoritmo es por tanto preferible al algoritmo Jarvis-March, ya que se excluye un tiempo de ejecución cuadrático. |
MICI - Círculo de referencia inscrito máximo (Maximum Inscribed Circle)
El cálculo del círculo de referencia MICIse basa en la función MaximumInscribedCircle. Con este procedimiento, el círculo de referencia se calcula como el círculo con el mayor diámetro posible que puede colocarse en el perfil desde el interior. También se conoce como círculo interior máximo. En este procedimiento, el círculo interior se corresponde, por tanto, con el propio círculo de referencia. El círculo exterior se obtiene como el círculo exterior más pequeño en relación con el centro del círculo de referencia. El círculo central se define aquí como el círculo promediado aritméticamente entre el círculo exterior y el círculo de referencia (es decir, el círculo interior).
MZCI - Círculos de referencia de la zona mínima
En el procedimiento MZCI, se determinan dos círculos de referencia. El cálculo se basa en la función MinimumZoneCircle. Se determinan dos círculos concéntricos que incluyen el perfil de redondez y tienen la menor distancia radial posible entre sí. Por tanto, los círculos de referencia están formados por el círculo exterior y el círculo interior. El círculo central se define aquí como el círculo promediado aritméticamente entre los dos círculos de referencia, es decir, el círculo exterior y el círculo interior.
Los parámetros adicionales Iteraciones e Incremento se utilizan para calcular el círculo MZCI. Para explicar los parámetros, resulta útil comprender el algoritmo MZCI: Los círculos concéntricos de referencia de la zona mínima se estiman en el primer paso de iteración utilizando los círculos interior y exterior calculados mediante el círculo de mínimos cuadrados (LSCI). A continuación, el resultado se mejora de forma iterativa. Se selecciona un nuevo punto alrededor del centro de los círculos concéntricos interior y exterior actuales utilizando una distribución normal bidimensional (la desviación típica se corresponde con el incremento). Se comprueba si los círculos concéntricos interior y exterior recalculados hasta el nuevo punto tienen una diferencia de radio menor que antes. Si es así, el punto se convierte en el nuevo punto central. A continuación, el procedimiento se repite iterativamente N veces en función del valor del parámetro Iteraciones y, por tanto, se mejoran sucesivamente los círculos de referencia de la zona mínima.
Los parámetros Iteraciones e Incremento disponen de las siguientes opciones de selección:
Iteraciones |
Descripción |
|---|---|
Automático |
El número de iteraciones se determina automáticamente (en función de los datos de entrada). |
Fijo |
El número de iteraciones puede especificarse explícitamente. Cuanto mayor sea el valor, más preciso será el resultado. |
Incremento |
Descripción |
|---|---|
Automático |
El incremento se determina automáticamente (en función de los datos de entrada). |
Fijo |
El incremento puede especificarse explícitamente. |
Determinar el centro del círculo calculando el valor medio de la trayectoria circular
Este procedimiento de aproximación circular es un procedimiento muy sencillo en el que el centro del círculo se determina calculando el valor medio de los componentes X e Y. Por tanto, el centro del círculo está establecido a priori. Por lo tanto, con este procedimiento no se determina un círculo de referencia. El círculo exterior se obtiene como el círculo exterior más pequeño en relación con el centro del círculo calculado y el círculo interior es el círculo interior más grande en relación con el centro del círculo calculado. El radio del círculo central se corresponde con el valor medio de las distancias de los puntos de datos al centro del círculo. Esto define el círculo central. Cabe señalar que el círculo central así calculado puede interpretarse como un valor estimado (inicial) para el círculo LSCI (y proporciona resultados similares). El uso de este procedimiento solo tiene sentido si los datos subyacentes se muestrean periódicamente (perfil cerrado).
Si se selecciona(n) círculo(s) de referencia como resultado, en su lugar se emiten todos los círculos (es decir, el círculo interior, central y exterior), ya que para este procedimiento no se dispone explícitamente de ningún círculo de referencia.
Nota Este procedimiento de aproximación circular elemental sigue el procedimiento de la norma ISO 7919-1, donde el centro del círculo también se calcula promediando los componentes X e Y (véase [3]). No obstante, cabe señalar que en la norma ISO-7919-1 no se define ningún círculo interior, central o exterior y, en consecuencia, la desviación de redondez, tal como se especifica arriba, no se calculó. De forma análoga a los procedimientos anteriores, los círculos interior, central y exterior, así como la desviación de la redondez, se presentan aquí como resultados por razones de simetría y comparación.
Además, se obtienen otros parámetros estadísticos que figuran en la norma ISO 7919-1 como medida para evaluar la trayectoria del eje. Estos son:
Parámetro |
Descripción |
|---|---|
Sxpp |
Valor pico a pico del componente X. |
Sypp |
Valor pico a pico del componente Y. |
SppMax_A |
Valor resultante de las amplitudes de vibración pico a pico medidas en dos direcciones ortogonales (véase el procedimiento A de la [sección B.3.2.1, 3]). |
SppMax_B |
Máximo de los dos valores pico a pico medidos en dos direcciones ortogonales (véase el procedimiento B de la [sección B.3.2.2, 3]). |
SMax |
Valor máximo de la amplitud de vibración (véase el procedimiento C de la [sección B.3.2.3, 3]). |
Prefiltrado mediante la eliminación de valores atípicos circulares
Los valores atípicos circulares pueden eliminarse de los datos antes de realizar la aproximación circular. Elimina todos los puntos de datos cuya distancia al Centro del círculo especificado sea mayor que el Radio mínimo ajustable y menor que el Radio máximo ajustable:
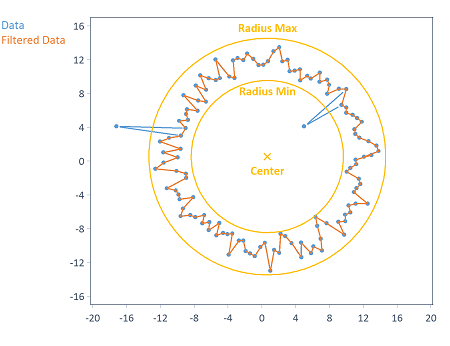
Las coordenadas X e Y del centro del círculo pueden calcularse automáticamente (como valor medio de los respectivos componentes X e Y de los datos de entrada) o especificarse explícitamente.
Prefiltrado con un filtro de Gauss
Antes de realizar la aproximación circular, el perfil de redondez puede prefiltrarse con un filtro de Gauss (véase [2]). Para ello se utiliza la función de GaussianFilter. Por razones matemáticas, los datos subyacentes deben muestrearse periódicamente para su filtrado (es decir, perfil cerrado).
Para el alisado del perfil se suele utilizar el filtro de Gauss (configuración del Tipo de filtro: Paso bajo). Al igual que en [2], el filtro de Gauss también puede utilizarse para el filtro paso alto. Un filtro paso banda de Gauss puede implementarse mediante la ejecución en serie de un filtro paso bajo y un filtro paso alto.
La Frecuencia de corte ajustable para el filtrado se especifica en la unidad UPR (U ndulations Per Revolution). Por ejemplo, 150 UPR corresponde a la vibración armónica número 150 de la frecuencia fundamental. Por lo tanto, también debe especificarse la frecuencia fundamental (normalizada). Corresponde al valor recíproco del número de puntos de datos por revolución. Las siguientes opciones están disponibles para especificar el Número de puntos de datos por revolución:
Configuración |
Descripción |
|---|---|
Calcular automáticamente |
El número de puntos de datos por revolución se calcula automáticamente mediante FlexPro utilizando la función Frequency. |
Longitud del conjunto de datos |
El número de puntos de datos por revolución se corresponde con el número de valores de los datos de entrada. |
Fijo |
El número de puntos de datos por revolución puede especificarse individualmente. |
El siguiente gráfico muestra un perfil suavizado con un filtro de Gauss (es decir, filtro paso bajo) con una frecuencia de corte de 50 UPR:
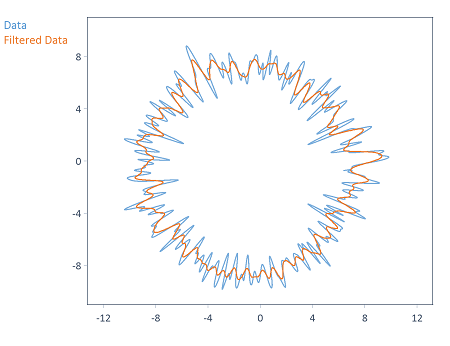
Datos como coordenadas polares
Los datos de entrada pueden estar disponibles tanto en coordenadas cartesianas como en coordenadas polares (radio y ángulo). Puede especificarlo en la pestaña Datos del objeto de análisis. El componente Y se corresponde con el radio y el componente X con el ángulo.
La Unidad angular dispone de los siguientes ajustes:
Configuración |
Descripción |
|---|---|
Automático |
La unidad del componente angular (componente X) se especifica en los datos de entrada y se toma de ellos. |
Grados |
La unidad del componente angular (componente X) debe interpretarse en grados. |
Radianes |
La unidad del componente angular (componente X) debe interpretarse en radianes. |
Si se dispone de una representación en coordenadas polares, los datos se transforman en coordenadas cartesianas antes del cálculo.
Sin embargo, los resultados siempre se muestran en coordenadas cartesianas, pero puede visualizarlos en un diagrama polar con transformación polar, como en el siguiente ejemplo:
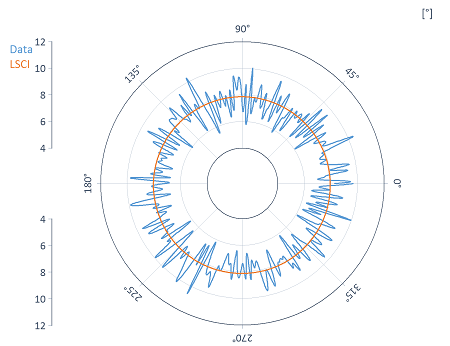
Bibliografía
[1] DIN Instituto Alemán de Normalización e.V.Parte 1: Vocabulary and parameters of roundness (DIN EN ISO 12181-1:2011), Geometrical product specifications (GPS)- Roundness, 2011.
[2] DIN Instituto Alemán de Normalización e.V.Parte 2: Specification operators (DIN EN ISO 12181-2:2011), Geometrical product specifications (GPS)- Roundness, 2011.
[3] DIN Instituto Alemán de Normalización e.V. Measurements on rotating shafts and evaluation criteria, Part 1: General guidelines (DIN ISO 7919-1:1996), 1996.
[4] Asociación de Ingenieros Alemanes. Form measurement - Principles for the measurement of geometrical deviations (VDI/VDE 2631), 1999.]
Funciones FPScript utilizadas
Véase también
* Este objeto de análisis no está disponible en FlexPro View y FlexPro Basic.