Este tutorial aborda los análisis espectrales en FlexPro relacionados con el modelado paramétrico autorregresivo y el análisis de valores propios. Estos métodos avanzados son especialmente adecuados para la estimación de frecuencias de conjuntos de datos pequeños.
Estimadores de frecuencia
Los estimadores espectrales AR y ARMA son procedimientos de modelización que utilizan un modelo autorregresivo (AR) o un modelo Autoregressive Moving Average (ARMA) para estimar los espectros de series temporales. El análisis utiliza los modos propios del ruido para construir un espectro de frecuencias ortogonal que contenga solo los componentes espectrales de banda estrecha de la señal. Los tres algoritmos son estimadores espectrales, es decir, proporcionan una estimación muy precisa de las frecuencias de los armónicos existentes. Sin embargo, la estimación de su potencia no suele ser exacta.
Extraer segmentos estacionarios
Dado que estos métodos exigen un gran esfuerzo de cálculo, son más útiles para conjuntos de datos pequeños en los que el análisis de Fourier requiere una resolución insuficiente. Como los datos de la señal también deben ser estacionarios, suele resultar últil extraer un pequeño rango del conjunto de datos en el que la señal sea aproximadamente estacionaria, es decir, que tenga un contenido espectral independiente del tiempo. En este tutorial, se utiliza una señal de prueba con una longitud de datos pequeña, que también podría ser un fragmento de un conjunto de datos mucho mayor.
Una señal de prueba adecuada
Para este tutorial se utiliza una señal de datos corta de longitud 64, con tres curvas senoidales que están demasiado juntas como para resolverse utilizando el análisis de Fourier.
100.0*sin(2π*x*420+π/2)
50.0*sin(2π*x*500+π)
100.0*sin(2π*x*580+3π/2)
La frecuencia de muestreo es de 5000 Hz, por lo que la frecuencia de Nyquist, la frecuencia máxima que se puede analizar, es de 2500 Hz. Todas las oscilaciones por encima de esta frecuencia se reflejan en frecuencias más bajas ("aliasing"). Los valores temporales varían de 0 a 0,0126 con un intervalo de muestreo de 0,0002. Se ha añadido un 10 % de ruido gaussiano aleatorio. El resultado es un ruido de fondo de aproximadamente -30 dB en relación con el pico más alto.
La amplitud de la onda senoidal central es la mitad de la de las otras dos ondas senoidales y tiene una cuarta parte de la potencia de las otras dos oscilaciones. Obsérvese que no se trata de un conjunto de datos de alto rango dinámico, sino de uno en el que los tres picos tienen una potencia significativa. El pico central está solo -6 dB por debajo de los otros dos picos. Por tanto, las optimizaciones en la gama de frecuencias tienen poco efecto en la resolución del pico medio.
Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Spectral Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Spectral Analysis.fpd. Abra la carpeta Tutorials y la subcarpeta Frequency Estimators y haga doble clic para abrir el diagrama 2D Data.
Esta es la representación de la señal, que tiene 64 valores en coma flotante.
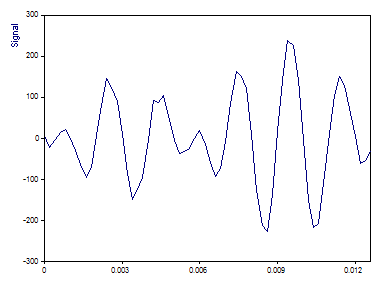
Espectro de Fourier
Utilizaremos una ventana de ponderación de Hamming que tenga la mejor atenuación posible del primer lóbulo lateral para la anchura unilateral del lóbulo principal de 2.
Cierre el diagrama y seleccione el conjunto de datos Signal.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis de Fourier en Análisis espectrales. Seleccione Espectro de Fourier. Pulse el botón Siguiente.
Observe que se selecciona el espectro de Fourier como procedimiento espectral. Aunque el procedimiento espectral ya se seleccionó en el paso 1, puede modificarse en el paso 2.
Seleccione el valor dB, normalizado como el tipo de espectro.
Esto significa que el pico más alto del espectro se normaliza a 0 dB. Todos los demás picos tienen un valor negativo. Un pico a -3 dB tendría la mitad de energía que un pico a 0 dB y un pico a -6 dB tendría la mitad de amplitud.
Seleccione Hamming -43 dB W=2 como Tipo de ventana.
En el módulo de análisis espectral, todas las ventanas de ponderación fijas no ajustables se listan por su nombre, la atenuación del lóbulo lateral en dB y el ancho del rango de Fourier unilateral. Una ventana rectangular equivale a no aplicar ninguna ventana, ya que todos los elementos de datos se multiplican por uno.
Asegúrese de que la longitud de la FFT está ajustada a la longitud de datos o a 64.
El campo de información Rellenado con ceros muestra que no se añaden ceros (zero padding).
Seleccione la opción Número máximo de picos e introduzca el valor 3.
El asistente para análisis genera automáticamente información sobre los picos del espectro. Si la opción está ajustada a 3, se muestran los tres picos de mayor potencia. Tenga en cuenta que también es posible especificar un valor dB umbral por debajo del pico más alto. Para este conjunto de datos podría establecer un valor umbral de -65 dB.
Ahora establezca Límite crítico ruido blanco % en Ninguno.
Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de frecuencia.
Puede elegir entre varias configuraciones. Puede activar el etiquetado para el componente Y del espectro (aquí en dB, normalizado) o para el componente X (siempre frecuencias). También puede desactivar el etiquetado.
El gráfico de Fourier en el asistente para análisis debería tener este aspecto:
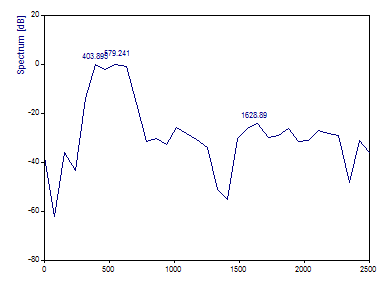
Establezca la Longitud de la FFT a 8192.
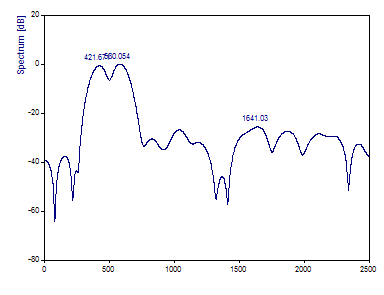
Añadiendo ceros, se reconocen mejor los picos de mayor potencia (a 420 y 580), pero la longitud de datos es demasiado corta para obtener una resolución de la curva senoidal de menor amplitud y frecuencia 500.8192 No se puede hacer nada para conseguir la resolución necesaria para el análisis de Fourier de este conjunto de datos. Debe muestrearse durante más tiempo. Ahora verá lo que ocurre cuando el mismo conjunto de datos se muestrea el doble de tiempo.
Haga clic en Cancelar. Seleccione el conjunto de datos Signal2.
Vuelva a hacer clic en el asistente para análisis. Seleccione la categoría Análisis de Fourier en Análisis espectrales. Seleccione Espectro de Fourier. Pulse el botón Siguiente. Ajuste Tipo de espectro a dB, normalizado, Tipo de ventana a Hamming -43 dB W=2, Longitud de la FFT a 8192, Número máximo de picos a 3, y Límite crítico ruido blanco % a Ninguno. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de frecuencia.
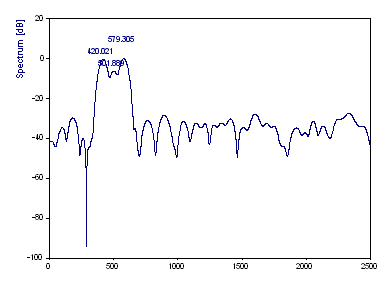
El componente de 420 Hz se detecta a 420,02, el de 500 Hz a 501,89 y el de 580 Hz a 579,30. El tercer pico tiene la potencia más alta y, por tanto, es de 0 dB. El primer pico es de -0,21 dB, el pico medio es de -6,20 dB.
Con esta longitud del conjunto de datos, la resolución es suficiente para determinar los tres componentes. Tenga en cuenta que la precisión de la estimación, tanto de la frecuencia como de la potencia, es muy buena, aunque está al límite de la resolución. El objetivo de este ejercicio era demostrar que es beneficioso estudiar detenidamente la viabilidad de utilizar el análisis de Fourier antes de considerar procedimientos alternativos.
Pero, ¿y si no es posible obtener más información mediante un muestreo más largo? Si los datos representan una instantánea más o menos estacionaria de una señal que cambia rápidamente, no es posible aumentar la resolución de frecuencia mediante un muestreo más largo. En tales casos, se requieren procedimientos de análisis AR, ARMA y de valores propios.
Estimación espectral AR
Los métodos de estimación espectral que se presentan a continuación son métodos potentes cuando la longitud de datos es demasiado corta para un análisis de Fourier suficiente.
Haga clic en Cancelar. Seleccione el conjunto de datos Signal utilizado originalmente. Tiene 64 valores.
Vuelva a hacer clic en el asistente para análisis. Seleccione la categoría Estimadores espectrales en Análisis espectral. Allí, seleccione Estimador espectral AR. Pulse el botón Siguiente.
Seleccione el algoritmo Matriz de datos FB SVD.
Los procedimientos de autocorrelación, Burg, ecuaciones normales FB y matriz de datos FB no ofrecen una separación integrada de la señal y el ruido. Se ofrecen en FlexPro con fines comparativos y porque estos procedimientos se han utilizado tradicionalmente para los análisis AR. Estos procedimientos pueden generar picos de interferencia, picos divididos y otras anomalías que pueden falsear el resultado del análisis. Por lo tanto, solo se recomiendan los dos algoritmos ecuaciones normales FB SVD y matriz de datos FB SVD.
El procedimiento Ecuaciones normales FB SVD puede utilizarse para acortar el tiempo de cálculo. Es considerablemente más rápido que el procedimiento Matriz de datos FB SVD para conjuntos de datos más largos.
Establezca el tipo de espectro en dB, el Orden en 40 y el subespacio de señal en 6.
El orden de 40 significa que se establece un modelo AR con 40 coeficientes. El subespacio de señal de 6 especifica que solo 6 modos propios deben tratarse como pertenecientes a la señal. Los otros 34 modos propios se consideran ruido y se suprimen en el cálculo SVD de los coeficientes AR. Esta separación integrada de señal y ruido elimina la influencia del ruido en el espectro.
Tenga en cuenta que debe aumentar el subespacio de señal en 2 por cada componente espectral adicional. Para asignar tres componentes espectrales, por ejemplo, el subespacio de señal debe establecerse en el doble, es decir, 6. Tenga en cuenta también que, en estos procedimientos, no es necesario especificar un número máximo de picos para etiquetar los picos en el espectro. Para los algoritmos sin SVD, este número resulta del número de raíces del polinomio AR y, para los algoritmos con SVD, del tamaño del subespacio de señal.
Seleccione la opción Tasa de muestreo adaptiva.
La opción Tasa de muestreo adaptiva genera un espectro con incremento adaptativo que se extiende por todo el rango de Nyquist. Así, los valores de frecuencia están próximos entre sí en la zona de los picos agudos y más separados en los puntos en los que la amplitud espectral está sujeta a cambios menores.
Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de frecuencia.
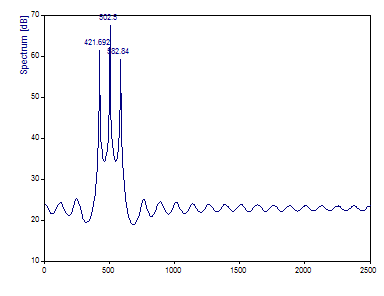
Aunque los armónicos intermedios no pueden determinarse con el análisis de Fourier, un análisis espectral AR bien ajustado puede resolver claramente los tres componentes espectrales. Los picos muy agudos son típicos de los armónicos en un espectro AR.
El componente de 420 Hz se estima en 421,69, la de 500 Hz en 502,5 y la de 580 Hz en 582,84. Aunque la comparación con los espectros de Fourier de los mismos datos (con 64 puntos) es impresionante, el análisis de Fourier proporcionaría una estimación más precisa de la frecuencia con una longitud de datos de 128. Obsérvese también que las cantidades de los picos AR son opuestas al perfil de potencia o amplitud. El componente medio tiene el valor más alto del espectro. Por lo tanto, el método AR debe considerarse principalmente solo como un estimador de frecuencia. Para estimar las amplitudes y potencias de los componentes, debe utilizarse el procedimiento del análisis armónico en dos etapas.
Seleccione el algoritmo Matriz de datos FB.
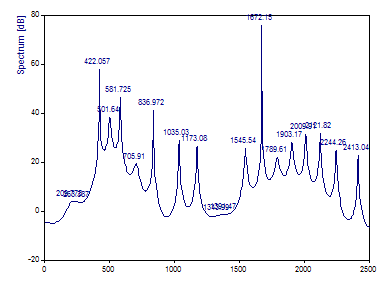
Esto demuestra lo que el análisis espectral AR convencional ha dado históricamente como resultado y por qué ha obtenido poco reconocimiento. A menos que se utilice una separación integrada de señal y ruido, un modelo AR suele producir la mitad de picos de los especificados en el orden del modelo, y no es raro que algunos de ellos estén distorsionados. Incluso se muestra un pico de ruido con un valor superior al de uno de los picos relevantes.
Seleccione el método de autocorrelación.
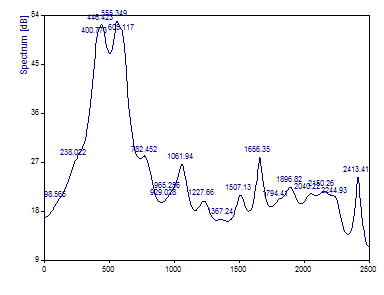
Dado que los filtros AR de este procedimiento son siempre estables (las raíces complejas del polinomio AR siempre se encuentran en o sobre el círculo unitario), los picos perturbadores del otro algoritmo AR habitual sin descomposición en valores singulares aparecen con menos frecuencia. Pero este método tiene una resolución de frecuencia significativamente peor. Como puede ver, este método AR no es adecuado para determinar el componente medio.
Espectros de análisis de valores propios
Los métodos de análisis de valores propios suelen considerarse los mejores estimadores espectrales. Los algoritmos MUSIC (Multiple Signal Classification) y EV (vector propio) se utilizan ampliamente para la estimación de componentes de banda estrecha en una señal.
Seleccione el procedimiento espectral Valores propios (MUSIC, EV) y el algoritmo MUSIC. Asegúrese de que el tipo de espectro está ajustado a dB, el orden está ajustado a 40 y el subespacio de señal tiene el valor 6. Mantenga la opción Tasa de muestreo adaptiva.

El componente de 420 Hz se estima en 422,32, la de 500 Hz en 501,56 y la de 580 Hz en 583,77. Aunque la comparación con los espectros de Fourier de los mismos datos (con 64 puntos) es impresionante, el análisis de Fourier proporcionaría también aquí una estimación más precisa de la frecuencia con una longitud de datos de 128.
Además, estas estimaciones no son tan precisas como el procedimiento AR. Aquí el componente medio tiene un valor menor. Aunque el perfil en este caso es correcto, el análisis de valores propios solo debe considerarse como un estimador de frecuencia. Para estimar las amplitudes y potencias de los componentes, debe utilizarse el procedimiento del análisis armónico en dos etapas.
Seleccione el algoritmo EV (EigenVector).
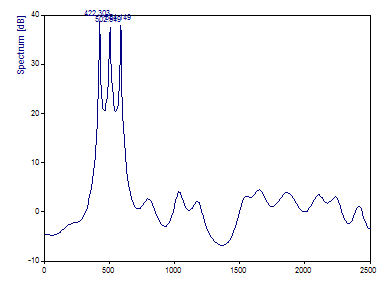
El componente de 420 Hz se estima en 422,30, el de 500 Hz en 502,55 y el de 580 Hz en 584,14. Para estos datos, el procedimiento MUSIC fue ligeramente mejor en la estimación de las frecuencias.
En estos procedimientos, los modos propios del ruido se utilizan para generar los espectros de señal. Por lo tanto, siempre debe haber un número elevado de modos propios del ruido para poder cartografiar adecuadamente el ruido de la señal. La única diferencia entre los algoritmos MUSIC y EV es la ponderación de los modos propios del ruido.
Análisis armónico
Ahora realizará un análisis armónico en dos etapas para determinar las amplitudes y potencias de los espectros.
Pulse el botón Atrás. Seleccione Análisis armónico y, a continuación, Estimación armónica. Haga clic en Siguiente.
Seleccione el algoritmo AR matriz de datos FB SVD, ajuste el Número de componentes a Como número máximo, el NMúmero máximo a 3 y el Tipo de espectro a Componentes armónicos. Establezca el Orden en 32.
En este procedimiento de dos etapas debe seleccionarse un orden bajo. Pueden producirse anomalías si el orden del modelo es superior a la mitad de la longitud del conjunto de datos. Para evitar estos efectos, que no pueden pasarse por alto fácilmente en este algoritmo automatizado de dos etapas, FlexPro limita automáticamente los órdenes del modelo en el espectro armónico a la mitad de la longitud del conjunto de datos.
Haga clic en Etiquetado hasta que aparezca el etiquetado de las amplitudes.
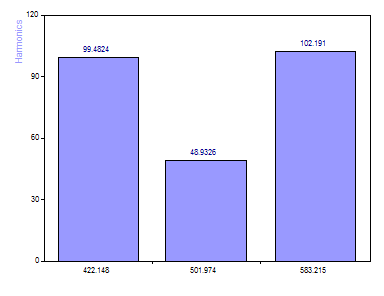
Se puede ver que las amplitudes [100, 50, 100] se han determinado con una precisión de unos pocos puntos porcentuales.
Haga clic en Siguiente. Seleccione todos los objetos del paso 3. Haga clic en Salir.
Haga doble clic en el objeto HarmonicAnalyse en la lista de objetos FlexPro.

Las fases utilizadas en la señal original son π/2, π, 3π/2. Es típico que los errores más pequeños se produzcan en las frecuencias y los más grandes, en las fases. Aquí la fase 1,57 es 1,49, la fase 3,14 es 2,94 y la fase 4,71 es 4,58. Son valores muy buenos si se tiene en cuenta que se ha añadido un 10 % de ruido a la señal de prueba.
Bibliografía
Encontrará una excelente presentación de los algoritmos espectrales AR en:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, pág. 172-284.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, pág. 153-270.
Encontrará una aplicación del algoritmo Burg en:
•W. H. Press, et. al, "Numerical Recipes in C", Cambridge University Press, 1992, pág. 564-575.
Encontrará una buena descripción de los algoritmos espectrales de análisis de valores propios en:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, pág. 361-378.
•Steven M. Kay, "Modern Spectral Estimation", Prentice Hall, 1988, pág. 429-434.
Véase también
Objeto de análisis Estimador espectral