Tutorial Ajuste de curva no lineal

Con el ajuste de curva no lineal es posible aproximar una función de modelo, en función de una variable independiente y de varios parámetros, a un conjunto de datos dado. La principal aplicación es la determinación de los parámetros del modelo, de forma que el modelo seleccionado se adapte mejor a los datos. Para ello es necesario conocer con precisión el modelo seleccionado y sus parámetros. Sin embargo, el ajuste de curva no lineal también puede utilizarse para interpolar o alisar un conjunto de datos determinado. En este caso, no importa qué modelo se utilice para el análisis. Tampoco es necesario comprobar los parámetros calculados del modelo. Una herramienta que compare los modelos disponibles entre sí (evaluación de modelo) resulta útil para este campo de aplicación.

Un ejemplo

Una pieza de plata se irradia con neutrones térmicos para producir los dos isótopos de plata de vida corta 47Ag108 y 47Ag110, que posteriormente vuelven a desintegrarse por emisiones beta. En el experimento, las partículas beta emitidas se cuentan a intervalos de 15 segundos durante un período de 4 minutos. El resultado es una curva exponencial decreciente, que se describe mediante la función de modelo Función exponencial decreciente (variante 2). El parámetro p0 se corresponde con la radiación de fondo, y p1 y p3 se corresponden con las amplitudes de los dos estados excitados con los tiempos de vida útil p2 y p4. Dado que el modelo es no lineal en los parámetros p2 y p4, se requiere un método de ajuste de curva no lineal.

Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Curve Fitting.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Curve Fitting.fpd. Abra la carpeta Example Silver y haga doble clic para abrir el diagrama 2D Ag-Diagram.

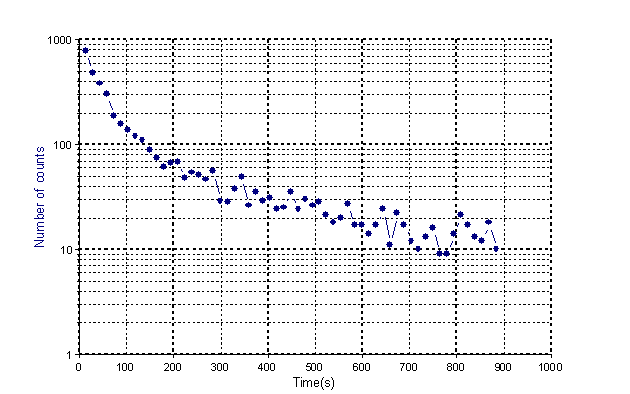
Este es un diagrama para la señal Ag con 59 valores en coma flotante. (Fuente: Bevington, p.142ff)

Evaluación de modelo

Cierre el diagrama y seleccione el conjunto de datos Ag, la señal que se va a analizar del experimento descrito anteriormente.

Haga clic en Insertar[Análisis] > Asistente para análisis.

Seleccione la categoría Ajuste de curva y, a continuación, Ajuste de curva no lineal. A continuación, pulse el botón Siguiente. Haga clic en Evaluación de modelo para determinar el modelo que mejor se aproxima al conjunto de datos seleccionado.

Se abre un cuadro de diálogo en el que puede seleccionar el algoritmo, el número máximo de llamadas a la función y las categorías de modelos. La asignación de las distintas funciones de modelo a las categorías se encuentra en Modelos. Seleccione Full-Newton como Algoritmo. Establezca el N.º máximo de llamadas a la función en 300 y seleccione todas las categorías. Cuanto mayor sea el valor de N.º máximo de llamadas a la función que seleccione, más modelos ofrecerán un resultado. Sin embargo, esto también aumenta el tiempo de cálculo del algoritmo. Haga clic en Siguiente.

Ahora se realiza un ajuste de curva no lineal para todos los modelos seleccionados y los modelos se clasifican y enumeran según la suma absoluta de cuadrados de los residuos SSE. Puede seleccionar en la lista el modelo que desea seguir utilizando. También se indica el coeficiente de determinación R2 calculado. R2 = 1,0 significa que la curva pasa por todos los puntos de datos. Con un valor X conocido, se puede determinar exactamente el valor Y correspondiente. R2 = 0,0 significa que el modelo de regresión no describe los datos mejor que una línea horizontal que pasa por el valor medio de los datos. Los valores X conocidos no ayudan a calcular el valor Y correspondiente.

Seleccione el modelo con la menor suma absoluta de cuadrados de los residuos, el Modelo NIST Hahn1, para lograr la mejor aproximación posible. Ahora cierre el cuadro de diálogo Evaluación de modelo pulsando Finalizar. Haga clic dos veces en Siguiente. Active la opción Diagramas y tablas que muestran el resultado. A continuación, haga clic en Finalizar.

Abra el diagrama de Señal recién creado para ver el resultado del alisado de señal. El siguiente diagrama muestra el resultado en escalado logarítmico.

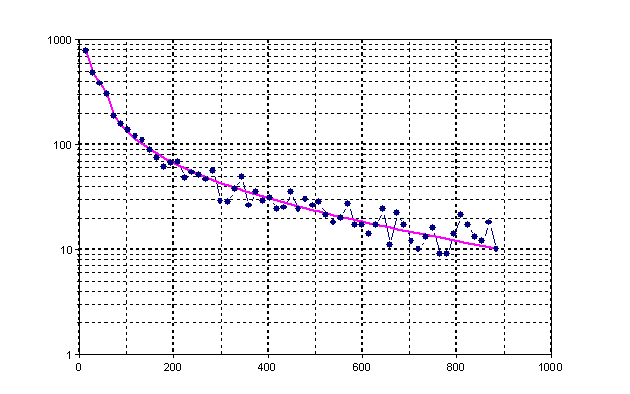
Aproximación lineal

Antes de determinar los parámetros del modelo mediante el ajuste de curva no lineal, la señal que se va a analizar se descompone y transforma de forma que pueda utilizarse una aproximación lineal para determinar los parámetros del modelo. Este método puede utilizarse para calcular los parámetros iniciales. En muchos casos, la elección de los parámetros iniciales es un criterio decisivo para el éxito del cálculo de los parámetros del modelo mediante el ajuste de curva no lineal. En este caso, el resultado de la linealización se utiliza para comprobar el resultado del ajuste de curva no lineal.

La función de modelo Función exponencial decreciente (variante 2) que se va a analizar tiene la forma:

Primero, se determina la radiación de fondo (parámetro p0). Basta con echar un vistazo a la curva de la señal para hacer una estimación aproximada. La curva exponencial se aproxima al offset que se va a determinar. Para una estimación aproximada de la radiación de fondo se promedian los tres últimos valores de la señal. El resultado es un valor 13,3. Para determinar los demás parámetros, se resta el offset de cada punto de la señal de entrada. La señal calculada se divide en dos subrangos A (x < 120) y B (x > 200). Los parámetros p3 y p4 se aproximan ahora mediante una transformación logarítmica y una aproximación lineal.

El componente de larga duración puede determinarse a partir de este resultado. Esta parte se resta ahora del ragno A para poder determinar el componente de vida corta. También se utiliza aquí una transformación logarítmica y una aproximación lineal.

Los parámetros determinados son los siguientes:

Abra la fórmula de Linearization en la carpeta Example Silver para ver la función FPScript para este cálculo.

Estimar parámetros

Tras esta estimación aproximada de los parámetros, se puede empezar con la determinación exacta de los parámetros del modelo.

Para ello, seleccione la señal Ag.

Seleccione Insertar[Análisis] > Asistente para análisis.

Seleccione la categoría Ajuste de curva y, a continuación, Ajuste de curva no lineal. A continuación, haga clic en Siguiente. Seleccione el modelo Función exp. decreciente (variante 2). También puede mostrar una Banda de predicción (95 %, 99 % o 99,9 %) y una Banda de confianza (95 %, 99 % o 99,9 %). La banda de confianza es útil para datos repetitivos, es decir, para cada valor X hay varios valores Y o hay un valor Y que representa el valor medio de varios puntos de medición. Un intervalo de confianza del 95 % es el intervalo Y para un valor X dado que contiene el verdadero valor Y con una probabilidad del 95 %. La banda de predicción hace una declaración sobre la dispersión de los datos que se van a analizar. Si se recogieran más puntos de datos, el 95 % de los puntos entrarían dentro del rango de la banda de predicción.

Una vez seleccionado el modelo, verá inmediatamente el resultado del ajuste de curva no lineal en la ventana de previsualización del asistente. El primer diagrama muestra la señal de entrada y la señal estimada. Los residuos se muestran en otro diagrama. En las dos tablas encontrará los parámetros estimados y una serie de valores estadísticos para analizar los resultados. Los parámetros del modelo calculados tienen los valores:

en este caso, p1 y p2 son los parámetros del componente de vida corta; p3 y p4 son los parámetros del componente de vida larga.

A continuación, haga clic en Siguiente. En esta página del asistente, el cálculo puede verse influido por varias opciones de configuración. Se puede seleccionar un algoritmo. También se pueden utilizar varios modos de ponderación y de escalado.

La opción de configuración más importante de esta página es la lista de Valores iniciales. Aquí pueden definirse los valores iniciales de los parámetros del modelo. También puede especificar si un parámetro tiene un valor fijo o no. También se puede especificar un límite inferior y superior para el algoritmo Full Newton.

La elección de los parámetros iniciales es decisiva para el resultado del cálculo. Si el punto de partida seleccionado está lejos del mínimo global, es posible que el algoritmo no devuelva ningún resultado o que devuelva un mínimo local diferente. Para aumentar la probabilidad de que el resultado mostrado sea un mínimo global, el cálculo debe realizarse con diferentes valores iniciales. La opción Estimar los valores iniciales está disponible para modelos con cuatro o menos parámetros. Para cada parámetro, se calculan 10 valores distribuidos aleatoriamente, que se encuentran dentro del rango definido por los límites inferior y superior. Ahora se calcula la suma absoluta de cuadrados de los residuos de cada combinación. La combinación con la menor suma de cuadrados proporciona los valores iniciales. Los valores iniciales de los parámetros también pueden calcularse mediante una fórmula FPScript. Los criterios de parade del algoritmo pueden verse influidos por las opciones de ajuste Nº máximo de llamadas de la funcion, Tolerancia X, Tolerancia Y, Tolerancia F y Tolerancia G. El cálculo de la primera iteración depende del límite de paso establecido.

En la última página del asistente, puede especificar qué diagramas, tablas y documentos deben crearse junto al objeto de análisis durante la evaluación. Seleccione la opción Diagramas y tablas que muestran el resultado para generar los diagramas y tablas que aparecen en la ventana de vista previa. Si desea visualizar la matriz de covarianza, la matriz de correlación, el error éstandar de los parámetros y el intervalo de confianza de los parámetros en forma tabular, seleccione también la opción Análisis tabulares adicionales. Pulse el botón Finalizar para salir del asistente.

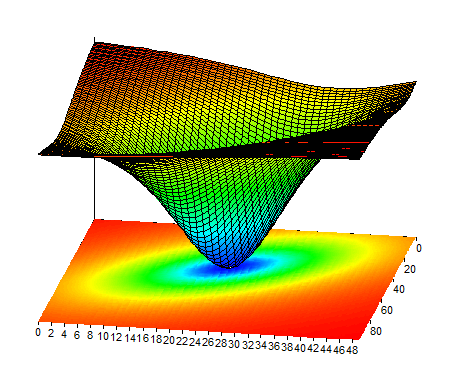
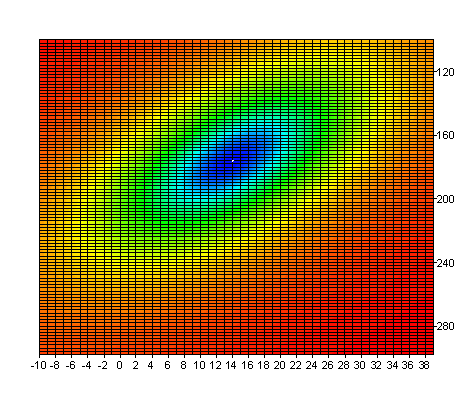
Para ilustrar que el resultado es un mínimo local, se calcula la suma absoluta de los cuadrados de los residuos del modelo en la fórmula Surface. Los parámetros p0 y p1 son variables, los parámetros p2, p3 y p4 son fijos. El resultado se muestra en el diagrama de superficie Surface. Se puede reconocer fácilmente que el mínimo está en p0 = 14 y p1 = 176.

Utilizar script de inicio

Este ejemplo muestra cómo puede utilizarse un script de inicio para calcular los valores iniciales de los parámetros del modelo.

Para ello, abra la fórmula de Linearization descrita anteriormente, seleccione el contenido de la fórmula (CTRL+A) y guárdelo en el portapapeles (CTRL+C). Seleccione la señal Ag.

Abra el asistente de ajuste de curva no lineal y vaya a la tercera página del asistente. Haga clic en el botón. Inserte el código script del portapapeles en el campo de entrada (CTRL+V). Haga clic en Ejecutar para comprobar el script. El resultado es una serie de datos con 5 valores en coma flotante de 64 bits. Haga clic en Aceptar para aceptar los valores calculados como valores iniciales. Si el número de valores calculados no se corresponde con el número de parámetros del modelo, no se aceptan los valores calculados. En lugar de insertar directamente el código script, también puede hacer referencia a una fórmula ya creada introduciendo el nombre de la fórmula en el campo de entrada. En este caso, sin embargo, el código solo es válido mientras exista el objeto de la fórmula.

Modelo personalizado

Además de los modelos predefinidos, es posible definir funciones de modelo propias y guardarlas en función del usuario. El siguiente ejemplo muestra cómo se crea un modelo personalizado. Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Curve Fitting.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025 >Examples>Tutorials>Curve Fitting.fpd. Abra la carpeta Custom Model y haga doble clic para abrir la fórmula Data. La fórmula calcula una señal mediante la función polinómica y =p0 + p1x + p2x² + p3x³. Se trata de una señal con 1000 valores en coma flotante de 64 bits.

Como esta función de modelo es lineal, los parámetros pueden calcularse utilizando la función FPScript Approximation (fórmula de Linear Approximation).

Para determinar los parámetros mediante el ajuste de curva no lineal, seleccione la fórmula Datos y elija Insertar[Análisis] > Asistente para análisis. Seleccione la categoría Ajuste de curva y, a continuación, Ajuste de curva no lineal. A continuación, haga clic en Siguiente. Introduzca el nombre Poly3 para un modelo personalizado en el cuadro de lista Modelo. Aparecen dos campos de entrada en los que se puede introducir la fórmula de la función de modelo o la fórmula de las derivadas parciales de la función de modelo. Escriba p[0] + p[1] * x + p[2] * x^2 + p[3] * x^3 en el campo de entrada de la función. p[0] a p[3] denotan los respectivos parámetros del modelo. Seleccione el valor 4 en el cuadro de lista Número de parámetros. Haga clic en Guardar modelo para guardar el modelo con el nombre especificado. Si en la ventana de vista previa aparece un mensaje de error en lugar del resultado deseado, deberá aumentar el Nº máximo de llamadas a la funcion en la página siguiente del asistente. A continuación, haga clic en Siguiente. Seleccione 300 llamadas a la función.

Pulse el botón Atrás. Para asegurarse de que las derivadas parciales se calculan analíticamente en lugar de numéricamente, debe introducir las fórmulas para las derivadas parciales en el campo de entrada Derivadas: [ 1, x, x^2, x^3 ]. Las derivadas parciales deben transferirse como una lista. El resultado de los parámetros estimados del modelo es ahora más preciso. Además, el número de iteraciones necesarias para el algoritmo Full-Newton se reduce considerablemente gracias al cálculo analítico de las derivadas parciales. Haga clic en Guardar modelo para volver a guardar el modelo.

También puede asignar nombres a los parámetros. Estos nombres se mostrarán en la lista Valores iniciales de la página siguiente del asistente. Para ello, debe modificar la fórmula que describe la función modelo personalizada del siguiente modo:

Dim p0 = p[0]
Dim p1 = p[1]
Dim p2 = p[2]
Dim p3 = p[3]
p0 + p1 * x + p2 * x^2 + p3 * x^3

La variable p[0] se asigna a la variable p0, la variable p[1] a la variable p1, y así sucesivamente. Debe asegurarse de que las asignaciones estén una debajo de la otra. Haga clic en Siguiente para ver la lista Valores de inicio con los parámetros renombrados.

Haga clic en Finalizar para salir del asistente.

Bibliografía

•P.R. Bevington, D.K. Robinson. Data Reduction and Error Analysis for the Physical Sciences, 3rd Ed., McGraw-Hill, New York, 2003.

•G. A. F. Seber, C. J. Wild. Nonlinear Regression. Wiley, Nueva York, 2003.

•Harvey Motulsky, Arthur Christopoulos. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, 2004.

Véase también

Asistente para análisis

Objeto de análisis Ajuste de curva no lineal

Opciones de salida estadística del ajuste de curva no lineal

Modelos no lineales