Este tutorial trata sobre los métodos espectrales ofrecidos por FlexPro para la modelización armónica y para medir la distorsión armónica.
Análisis de Fourier
Si aún no ha visto el tutorial Análisis de Fourier y el tutorial Estimador espectral, debería hacerlo ahora. El primer paso del análisis armónico es una estimación espectral totalmente automatizada, que suele realizarse mediante el análisis de Fourier, el estimador espectral AR o el análisis de valores propios.
Una señal de prueba armónica con distorsión y ruido
Para este tutorial se utiliza una señal con 1024 valores. La señal tiene una onda fundamental y una serie de armónicos en los múltiplos de la frecuencia del primer armónico:
100.0*sin(2π*x*250+π/4)
10.0*sin(2π*x*500+π/2)
1.0*sin(2π*x*750+π)
0.1*sin(2π*x*1000+3π/2)
0.01*sin(2π*x*1250+7π/4)
La frecuencia de muestreo es de 5000 Hz, por lo que la frecuencia de Nyquist, la frecuencia máxima que se puede analizar, es de 2500 Hz. Los valores de tiempo varían de 0 a 0,2046 con un intervalo de muestreo de 0,0002. Se agrega un 0,01 % de ruido blanco. El resultado es un ruido de fondo a un nivel de -100 dB en relación con el pico más alto.
Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Spectral Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Spectral Analysis.fpd. Abra la carpeta Tutorials y la subcarpeta Harmonic Analysis y haga doble clic en Data para abrir el diagrama 2D.
Aquí puede ver la ilustración de la señal, que tiene 1024 valores en coma flotante.
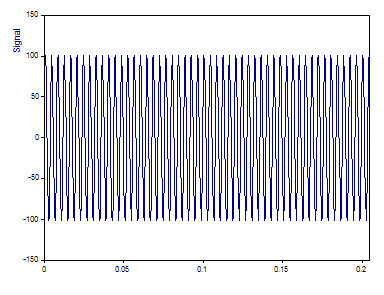
Solo la onda fundamental es reconocible en el dominio del tiempo. Los armónicos causan una distorsión armónica significativa.
Observe primero el espectro de Fourier de la señal, aunque es posible determinar el número de componentes armónicos sin él.
Espectros de Fourier
Cierre la ilustración y seleccione el conjunto de datos Señal.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis de Fourier en Análisis espectrales. Allí se selecciona Espectro de Fourier. Pulse el botón Siguiente.
Seleccione dB, normalizado como Tipo de espectro. Seleccione Chebyshev como Tipo de ventana e introduzca 4 como parámetro ajustable. Asegúrese de que la Longitud de la FFT está establecida en 16384. Seleccione la opción Número máximo de picos e introduzca el valor 5. A continuación, establezca Límite crítico ruido blanco % en Ninguno. Si no hay ningún etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezcan los valores en decibelios.
La visualización del espectro de Fourier en el asistente para análisis debería tener este aspecto:
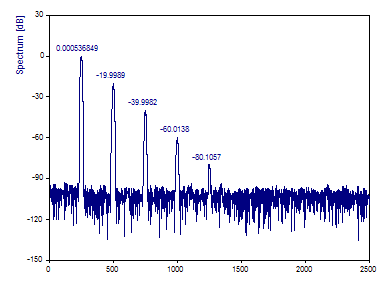
Los armónicos están suficientemente caracterizados por el espectro de Fourier.
Haga clic en Etiquetado hasta que se muestren las frecuencias.
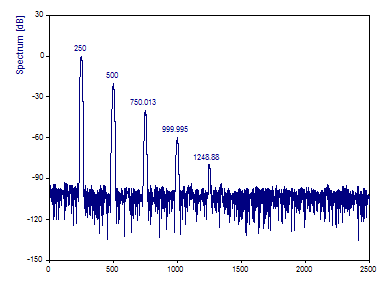
Por tanto, las frecuencias de la onda fundamental y de los armónicos se estiman con suficiente precisión mediante este espectro de Fourier optimizado.
Métodos de Fourier para la identificación de frecuencias
Los ajustes utilizados para el espectro de Fourier representan los ajustes que se utilizan automáticamente en el análisis armónico. El análisis armónico utiliza el análisis de Fourier para la identificación de frecuencias. En todos los casos, se utiliza la función de ventana Chebyshev y su ancho unilateral del lóbulo principal se ajusta automáticamente. Para datos de longitud 256 o inferior, el ancho se fija en 2. Para longitudes de datos superiores a 1024, el ancho de ventana es 4. Entre estos valores, los ajustes de la ventana varían logarítmicamente con (-6+1,4427ln(n)). Por ejemplo, se utiliza un ancho del dominio de la frecuencia de 3 para una longitud del conjunto de datos de 512. El rellenado con ceros (zero padding) se utiliza para obtener una longitud de la FFT de 16384 si la longitud del conjunto de datos es inferior a 16384.
El uso del análisis de Fourier para la identificación de frecuencias tiene dos inconvenientes. La estimación espectral exacta puede ser peor que el procedimiento AR o el análisis de valores propios, incluso si se utilizan funciones de ventana, rellenado con ceros e interpolación de bandas. Esto se aplica sobre todo si el conjunto de datos solo tiene mil puntos o menos. El análisis de Fourier para la identificación de frecuencias no es recomendable si el conjunto de datos es muy pequeño, es decir, si solo tiene unos cientos de valores.
Igual de importante es el hecho de que el análisis de Fourier a menudo provoca algunos lóbulos laterales pronunciados en la subida y bajada de un pico grande. La ventana de Chebyshev se ha utilizado para minimizar este efecto. Aun así puede producirse, especialmente cuando se aplica el rellenado con ceros para mejorar la estimación de la frecuencia. Aunque el análisis armónico también puede incluir algunos componentes que solo modelan el ruido pero que, por tanto, mejoran la precisión de la modelización para los componentes de la señal, debe garantizarse que dichos picos parásitos en los hombros de los picos principales no se incluyan en el modelo.
Este es el espectro de Fourier, exactamente igual que el anterior, salvo que se ha utilizado la ventana Blackman-Harris de -92 dB. Se reconocen 10 picos.
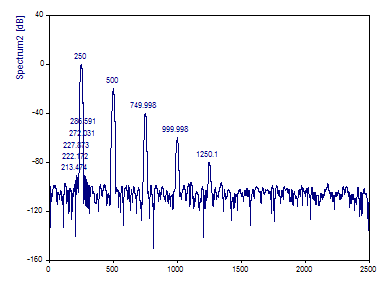
Puede ver que los cinco picos adicionales se producen todos en el rango del pico del primer armónico. En tal caso, no es posible agregar armónicos adicionales para simular el ruido. Aquí es importante que solo se incluyan cinco armónicos en el modelo.
Estimación armónica
El objetivo del análisis armónico es modelar una señal con curvas senoidales de banda estrecha o curvas senoidales amortiguadas. El resultado del análisis es un número determinado de armónicos, que se definen por amplitud, frecuencia, fase y, en el caso de curvas senoidales amortiguadas, factor de amortiguamiento.
Haga clic en Atrás. Seleccione la categoría Análisis armónico en Análisis espectral. Seleccione Estimación armónica. Pulse el botón Siguiente. Seleccione Fourier como Algoritmo y Senoidal como Modelo. Ajuste el número de componentes a Como número máximo e introduzca 10. El tipo de resultado es Componentes armónicos. Haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
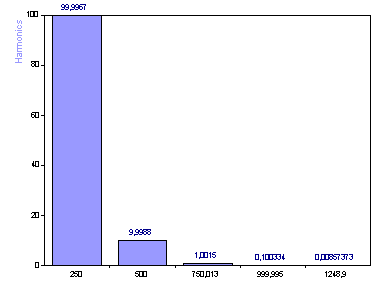
Aunque es posible leer los valores de amplitud a partir del etiquetado, no es una buena representación. La escala logarítmica es necesaria para mostrar claramente el amplio rango dinámico de las amplitudes.
Haga clic en el botón Siguiente para ir al paso 3 del asistente. Active la casilla superior y seleccione el diagrama 2D con el nombre Armónicos. Seleccione el eje Y logarítmico. Haga clic en Atrás para volver al paso 2 del asistente.
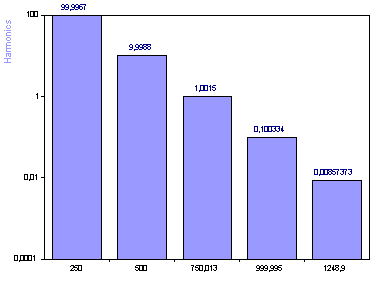
La modelización armónica consta de dos pasos. El primer paso, el análisis de Fourier, solo se utiliza para estimar las frecuencias en las que se producen los componentes espectrales. La información de amplitud o potencia del espectro de Fourier no se utiliza en el análisis armónico. En este caso, se utilizó el análisis de Fourier para determinar las 10 frecuencias de los componentes espectrales más significativos. El espectro armónico mostrado aquí se basa en una aproximación lineal de curvas senoidales en el dominio del tiempo. Las cuatro primeras amplitudes se determinaron con gran precisión. El quinto armónico tiene un error superior al 10 %. Los armónicos restantes modelan el ruido presente en la señal. Dado que el ruido blanco se distribuye uniformemente en todas las frecuencias, pero esto no se modela en consecuencia aquí, el número de armónicos debe reducirse al número de componentes espectrales reales.
Aunque los cinco picos de la señal se apreciaban claramente al examinar visualmente el espectro de Fourier, esto no resulta tan claro en el análisis armónico basado en las frecuencias espectrales determinadas a partir del espectro de Fourier. No hay una distinción clara entre señal y ruido.
Seleccione el Algoritmo AR matriz de datos FB SVD. Establece el orden del modelo en 40.
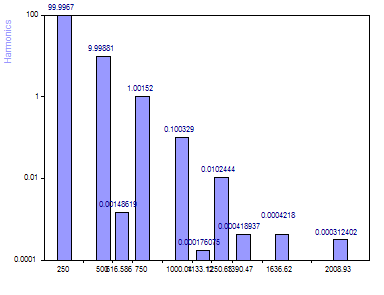
Cuando se utiliza el algoritmo AR SVD para la identificación de frecuencias, hay cinco componentes únicos por encima del nivel de ruido de fondo. Además, las amplitudes están mejor determinadas por las funciones senoidales lineales, ya que las frecuencias están mejor estimadas. Los armónicos adicionales también se distribuyen de forma más uniforme en todas las frecuencias, como cabría esperar de un ruido aleatorio.
Seleccione el algoritmo Análisis de valores propios MUSIC.
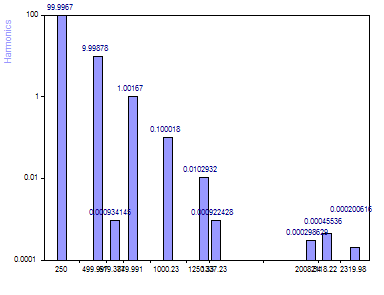
Cuando se utiliza el algoritmo MUSIC de análisis de valores propios para la identificación de frecuencias, también hay cinco componentes únicos por encima del nivel de ruido de fondo. La precisión de la determinación de la amplitud es similar a la del método AR.
El método AR SVD utiliza los modos propios de la señal para la estimación espectral. El análisis de valores propios siempre utiliza los modos propios del ruido para la estimación espectral. Uno de los dos puede conducir a un resultado más preciso. Por lo tanto, a menudo deben investigarse ambos casos. Tenga en cuenta que ambos procedimientos reconocen bien las cinco frecuencias de la señal. Los cinco armónicos para la modelización del ruido se solapan ligeramente.
Parámetros de los componentes armónicos
El ruido blanco no debe estar correlacionado. Esto significa que no se pueden hacer afirmaciones sobre la tendencia o la duración de la señal de ruido. La amplitud del ruido en una frecuencia discreta no debe afectar en modo alguno a la amplitud de la frecuencia siguiente. Si el ruido no está completamente correlacionado, los armónicos adicionales utilizados para el ajuste del ruido no sirven de nada.
Para modelar solo los cinco primeros componentes de la señal, establezca el Número máximo en 5.
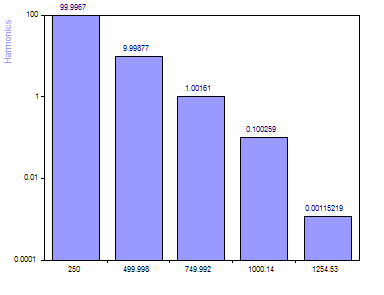
Puede ver que el armónico de menor potencia (amplitud 0,01) ya no se estima con exactitud. De hecho, su amplitud ha disminuido casi una décima con respecto al valor real. Mientras que con diez armónicos especificados se disponía de cinco disponibles para modelar la señal de ruido, ahora solo quedan los cinco componentes de la señal de ruido. El ruido tiene un efecto perjudicial en el armónico de menor potencia.
Vuelva a establecer el número máximo en 10. Haga clic en Siguiente. En el paso 3, seleccione las dos primeras opciones y haga clic en Finalizar. Haga doble clic en Análisis armónico .
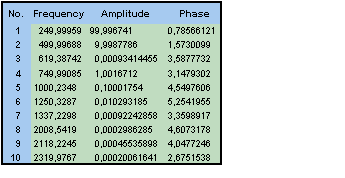
Las frecuencias, amplitudes y fases de los cinco componentes de la señal se estimaron con bastante precisión. Una característica típica de la modelización armónica es que las frecuencias tienen el menor error y las fases el mayor. Los errores de amplitud se sitúan en un punto intermedio. Cuanto mayor sea la potencia de un componente, con mayor precisión podrán determinarse los parámetros que definen los armónicos.
Distorsión armónica
El factor de distorsión (THD = total harmonic distortion) es la relación entre la raíz de la suma de todas las potencias o amplitudes al cuadrado de los armónicos y la amplitud de la onda fundamental.
Los FFT suelen utilizarse para medir el factor de distorsión. Debido al desbordamiento de los valores espectrales vecinos durante la ponderación de ventana o debido al manchado espectral que se produce cuando no se utiliza ninguna ventana de ponderación, calcular el factor de distorsión exacto utilizando la FFT es muy difícil. Esto se aplica sobre todo si se va a ignorar el ruido y solo se van a incluir los armónicos de la señal.
La modelización armónica de FlexPro permite obtener una estimación precisa del factor de distorsión (THD). El valor verdadero de esta señal de prueba es sqrt(10²+1²+0,1²+0,01²) / 100. Es decir, el 10,05 %.
Los ajustes utilizados para la modelización armónica también pueden utilizarse para un espectro de factor de distorsión.
Seleccione el registro de datos Signal.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis armónico en Análisis espectral. Seleccione Estimación armónica. Pulse el botón Siguiente.
Seleccione el Algoritmo MUSIC de análisis de valores propios y el Modelo Senoidal. Establezca Como número máximo de componentes en 5. Seleccione Espectro de factor de distorsión en % como Tipo de espectro. Haga clic en Etiquetado hasta que aparezcan las distorsiones en %.
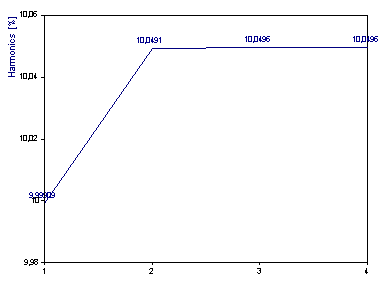
El número de componentes se muestra en el eje x. En el 2.º componente la distorsión armónica se muestra en función de la relación entre el primer armónico y la onda fundamental. El componente 3 muestra la distorsión acumulada resultante del primer y segundo armónico. El valor en la posición 4 es, por tanto, el factor de distorsión (THD) sin ruido. El valor 10,0497 está muy cerca del valor correcto 10,0504. Si ajusta el número de componentes a 10, verá que los cinco armónicos adicionales para modelar el ruido no contribuyen significativamente al factor de distorsión.
Haga clic en Salir para cerrar el asistente para análisis.
Véase también
Objeto de análisis Análisis armónico
Algoritmos de análisis de valores propios