La transformada de ondícula continua (CWT = Continuous Wavelet Transform) se utiliza para dividir una señal en ondículas. Las ondículas son oscilaciones que se producen en un corto período de tiempo. Mientras que la transformada de Fourier descompone una señal en oscilaciones senoidales y cosenoidales sin restricciones de tiempo y, por tanto, pierde toda información sobre la localización temporal, las funciones elementales de la CWT son versiones escaladas y desplazadas de la ondícula madre localizada en el tiempo. La CWT se utiliza para crear una representación de tiempo-frecuencia de la señal que tiene una alta resolución de tiempo-frecuencia.
La CWT es una herramienta excelente para cartografiar las características cambiantes de las señales no estacionarias. También es adecuada para comprobar la estacionariedad. Si una señal resulta ser no estacionaria, la CWT puede utilizarse para detectar secciones estacionarias de la señal.
Los cálculos básicos en los procedimientos CWT de FlexPro siguen los algoritmos de Torrence y Compo. La nomenclatura de las ecuaciones siguientes corresponde también a la publicación de Torrence y Compo que figura abajo.
Transformación continua de ondículas
La CWT se basa en las siguientes definiciones:
La CWT es una convolución de la serie de datos con una versión escalada y desplazada de la ondícula madre, la función Ψ. Esta convolución puede calcularse directamente, como se muestra en la primera ecuación, o mediante una convolución rápida basada en la FFT, como se muestra en la segunda ecuación.
Obsérvese que la CWT es una función continua, a excepción de la serie de datos discretos x y su transformada discreta de Fourier. En estas ecuaciones, * simboliza una conjugación compleja, N es la longitud de la serie de datos, s es el factor de escala de la ondícula, δt es el intervalo de muestreo, n es el índice de tiempo localizado y ω es la frecuencia angular. Cada una de las ecuaciones incluye una normalización para que la ondícula tenga la misma energía en cada escalado.
Con la CWT, se calcula la correlación entre la ondícula y los segmentos sucesivos de la serie de datos para cada factor de escala seleccionado. Mientras no se requiera reconstrucción, no hay restricciones en cuanto al número de factores de escala y sus incrementos. Un espectro CWT puede utilizar un escalado lineal o logarítmico a cualquier densidad deseada. Si es necesario, se puede calcular un espectro de alta resolución para un dominio de la frecuencia reducido. Las convoluciones pueden calcularse hasta N veces para cada escalado y deben calcularse para todas las N si se utiliza una FFT. La CWT consta de N valores espectrales para cada valor de escala utilizado y cada uno de ellos requiere una FFT inversa. El esfuerzo de cálculo y los requisitos de memoria son, por tanto, considerables. La ventaja de esta alta redundancia en la CWT es un espectro de tiempo-frecuencia preciso.
Funciones elementales de ondícula (ondículas madre)
A diferencia de la descomposición de Fourier, que utiliza funciones exponenciales complejas como funciones elementales, la descomposición de ondículas utiliza ondículas madre localizadas en el tiempo. La función de ondículas madre es continua tanto en tiempo como en frecuencia y sirve como función de salida para la construcción de las funciones elementales escaladas y desplazadas. La ondícula madre puede ser compleja o real y, en ambos casos, dispone de un parámetro de ajuste con el que se pueden fijar las propiedades de la oscilación. El análisis de ondículas es más difícil que el análisis de Fourier porque primero hay que definir la ondícula madre, a partir de la cual se construyen las funciones elementales. FlexPro ofrece tres ondículas madre diferentes, cada una en una versión compleja y otra real.
Ondícula de Morlet
La ondícula más utilizada es la ondícula de Morlet, una oscilación senoidal compleja con ponderación gaussiana, que se define como sigue en el dominio del tiempo y la frecuencia:
En estas ecuaciones, η es un parámetro de tiempo adimensional, m es el número de onda y H es la función de Heaviside.
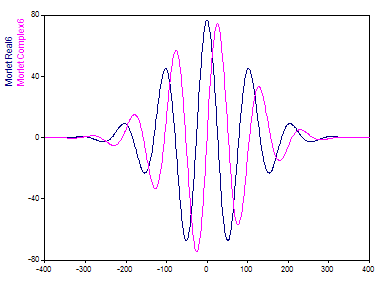
La siguiente representación en el dominio del tiempo muestra la parte real y la parte imaginaria de una ondícula de Morlet con un parámetro de ajuste (número de onda) de 6:
El parámetro de ajuste de la ondícula de Morlet, el número de onda, puede variar de 6 a 100 en FlexPro. Un número de onda de 20 conduce a la siguiente representación en el dominio del tiempo:
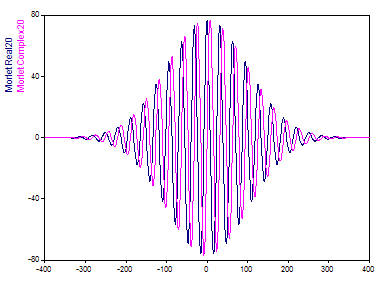
El número de oscilaciones en la ondícula de Morlet corresponde aproximadamente al número de onda.
Ondícula de Paul
FlexPro también ofrece la ondícula de Paul:
La ondícula de Paul decae más rápidamente. El parámetro de ajuste de la ondícula de Paul es un orden que puede especificarse para FlexPro en el rango de 4 a 40. Con un orden de 4, solo hay una oscilación en la ondícula:
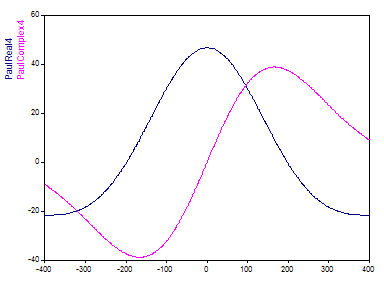
Incluso con el orden más alto disponible de 40, la ondícula de Paul solo muestra un número de oscilaciones que corresponde al número de onda más bajo de la ondícula de Morlet:
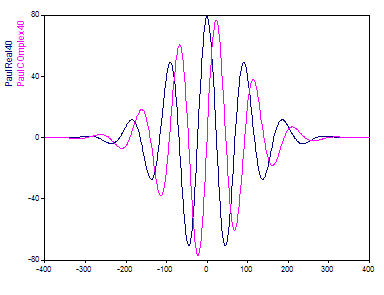
La ondícula de Paul ofrece una mejor localización temporal que la de Morlet, ya que decae más rápidamente en el dominio del tiempo. A diferencia de la ondícula de Morlet, su representación en el dominio de la frecuencia no es un pico simétrico, sino uno desplazado hacia la derecha hacia las frecuencias más altas. Se asemeja a un pico gamma y la asimetría disminuye a medida que aumenta el orden. Sin embargo, incluso con el orden más alto disponible de 40, muestra una clara desviación del pico principal en el dominio de la frecuencia. Por tanto, la ondícula de Paul ofrece una resolución de frecuencia más baja.
Ondícula derivada gaussiana
La tercera ondícula admitida por FlexPro es la ondícula derivada gaussiana. La parte real se define del siguiente modo:
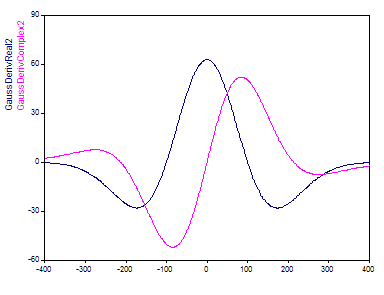
La ondícula compleja se crea añadiendo una función de Heaviside en el dominio de la frecuencia. Esta ondícula decae con la raíz cuadrada de la función gamma. Su localización temporal se sitúa entre la de la ondículas de Morlet y la de Paul. El parámetro de ajuste es el orden de la derivada y puede variar de 2 a 80 en FlexPro. La derivada más pequeña de 2 se conoce como la ondícula "Marr" o "Mexican Hat". La ondícula contiene una sola oscilación:
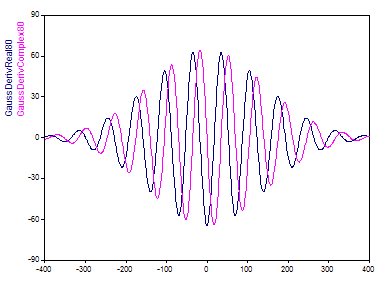
Con el mayor parámetro de ajuste de 80, la ondícula derivada gaussiana contiene aproximadamente tantas oscilaciones como la ondícula de Morlet con un número de onda de 12:
Visualización en el dominio de la frecuencia
Las transformaciones en el dominio de la frecuencia de las ondículas madre (de Morlet con número de onda 6, de Paul con orden 40 y derivada gaussiana con orden 20) dan como resultado la siguiente representación:
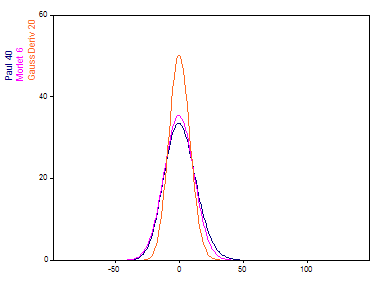
Si se ajusta el parámetro de ajuste de las tres ondículas de modo que contengan aproximadamente seis oscilaciones, la ondícula derivada gaussiana muestra la representación de frecuencias más compacta. La ondícula de Paul muestra el pico más ancho y la de Morlet se sitúa entre ambas.
La transformada de Fourier de una ondícula de Morlet produce un pico simétrico, la representación espectral de la ondícula derivada gaussiana es un pico gamma exacto y la asimetría a la derecha es significativamente menor que la de la ondícula de Paul, y casi desaparece para un orden de derivada superior a 20. (Los valores más altos de la derivada de la ondícula derivada gaussiana muestran picos espectrales casi gaussianos.)
Resolución temporal comparada con la resolución de frecuencia
Las tres ondículas madre muestran una muy buena localización temporal de la oscilación debido a su rápido decaimiento. Para un número determinado de oscilaciones, la ondícula de Paul localiza con mayor eficacia en el dominio del tiempo. La ondícula de Morlet es ligeramente menos eficaz y la ondícula derivada gaussiana muestra la localización temporal más baja de las tres. Sin embargo, al comparar las resoluciones de frecuencia, la ondícula derivada gaussiana obtiene los mejores resultados y la ondícula de Paul, los peores. También aquí la ondícula de Morlet se sitúa en medio.
Aunque la ondícula de Morlet no es tan compacta como la derivada gaussiana para un número determinado de oscilaciones, se puede establecer un número de oscilaciones mucho mayor. Esto permite lograr una mayor resolución de frecuencia con la ondícula de Morlet.
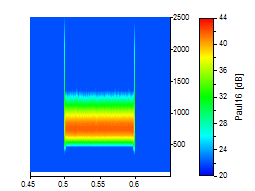
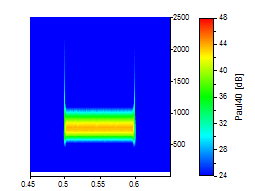
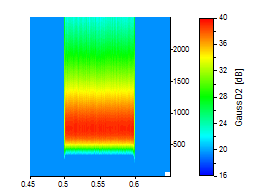
La mejor forma de ilustrarlo es gráficamente. Los siguientes análisis de ondículas utilizan un conjunto de datos ruidosos en los que se produce una oscilación senoidal simple en el dominio del tiempo de 0,5 a 0,6:
La cima del pico se amplió para que quedara claro el compromiso en la resolución de tiempo-frecuencia. Todos los gráficos utilizan la misma escala para los ejes de tiempo y frecuencia. Se utilizó una ondícula de Morlet con los números de onda 6, 20 y 50 para las tres primeras imágenes:
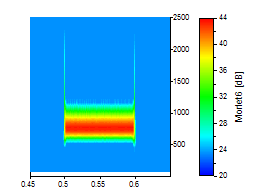
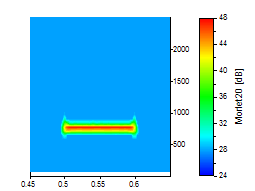
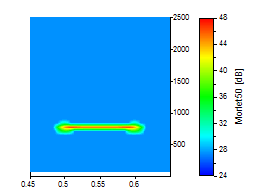
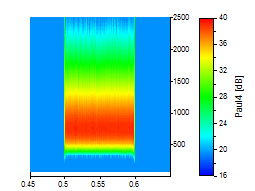
Se utilizó una ondícula de Paul con órdenes de 4, 16 y 40 para las tres imágenes siguientes:
Se seleccionó una ondícula derivada gaussiana de órdenes 2, 20 y 80 para las tres últimas imágenes:
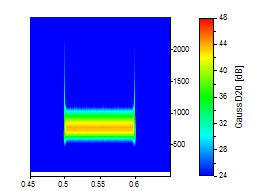
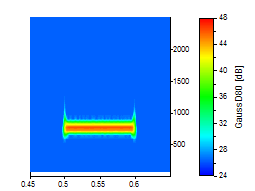
Si no se requiere una resolución temporal óptima, la ondícula de Morlet suele ser una buena opción, ya que proporciona una buena resolución tanto para la frecuencia como para el tiempo.
La resolución de frecuencia de la ondícula de Paul de orden 40 corresponde aproximadamente a la ondícula de Morlet con su número de onda más bajo, 6. En los ejemplos de la ondícula de Paul, también se puede reconocer la asimetría en la frecuencia. Sin embargo, si lo que le interesa es una resolución temporal óptima, la ondícula de Paul es una buena elección.
En su resolución de frecuencia más alta (orden 80), la ondícula derivada gaussiana se acerca a la ondícula de Morlet con un número de onda de 12. A diferencia de la ondícula de Paul, los órdenes superiores son casi simétricos y la resolución de frecuencia puede superar a la de la ondícula de Morlet en números de onda bajos.
Análisis "multirresolución"
Con la transformada rápida de Fourier, la longitud fija del segmento controla la relación entre la resolución temporal y de frecuencia. El resultado es una resolución temporal y de frecuencia constante e independiente de la frecuencia que se desee visualizar. En cambio, la CWT es un análisis de resolución variable. Este análisis "multirresolución" se desarrolló para el caso frecuente de que los componentes de la señal con una frecuencia alta solo existan durante breves períodos de tiempo, mientras que los componentes de baja frecuencia son más persistentes.
Los componentes de alta frecuencia y corta duración requieren una buena localización temporal. Para lograrlo, se reduce la resolución de frecuencia. Por otra parte, los componentes de larga duración y baja frecuencia toleran una resolución temporal menor, pero requieren una resolución de frecuencia mayor. Los componentes espectrales de baja frecuencia suelen constituir la mayor parte de la señal y se cuantifican mejor cuando la resolución de frecuencia es lo más alta posible.
El análisis multirresolución evita el difícil problema de la longitud óptima de los segmentos. El ancho de los segmentos temporales varía automáticamente con la frecuencia. Sin embargo, esto es obviamente una desventaja si una señal tiene componentes efímeros de baja frecuencia. La transformación rápida de Fourier suele ser la mejor opción para este tipo de señales. Esta variación en la resolución de frecuencia también hace imposible leer las potencias o amplitudes espectrales directamente a partir del espectro de ondículas. También en este caso, la STFT tiene ventajas sobre la CWT.
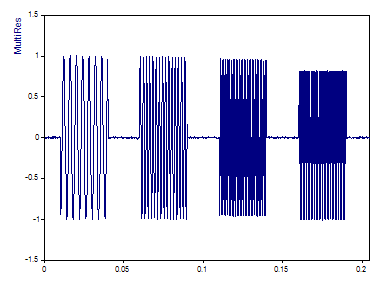
El siguiente conjunto de datos contiene una secuencia de oscilaciones senoidales de la misma potencia con un ruido del 1 %. En el intervalo de tiempo de 0,01 a 0,04 hay una frecuencia de 250 Hz, de 0,06 a 0,09 una frecuencia de 500 Hz, de 0,11 a 0,14 una frecuencia de 1 KHz y en el intervalo de 0,16 a 0,19 una frecuencia de 2 KHz.
En el espectro siguiente se utilizó una ondícula de Morlet con un número de onda de 12:
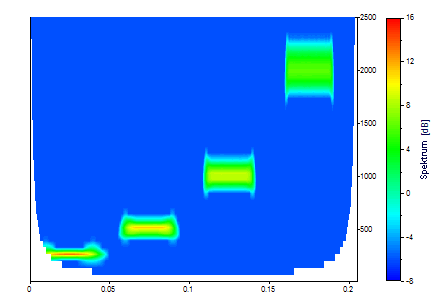
La resolución variable es claramente reconocible. El componente de 250 Hz está muy bien resuelto en frecuencia, pero es muy poco nítido en tiempo. Por el contrario, el componente de 2000 Hz se representa nítidamente en el tiempo, pero tiene una frecuencia borrosa.
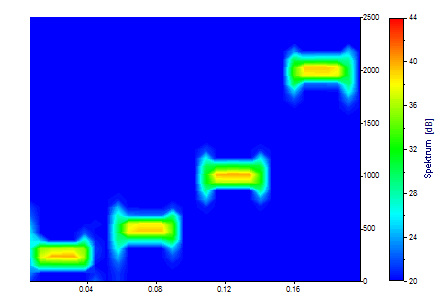
Como comparación, he aquí una STFT optimizada. La resolución fija de la STFT es claramente visible:
Añadir ceros y el "Cone of Influence"
Al calcular el espectro CWT, primero se calcula una FFT de la serie de datos. A continuación, se calcula la respuesta de frecuencia de la ondícula para cada escalado (frecuencia deseada) del espectro y se multiplica por el espectro del conjunto de datos. El producto se transforma de nuevo.
Las transformadas de Fourier requieren datos periódicos. Para garantizar que la convolución rápida mediante FFT no presente efectos de aliasing causados por la no periodicidad de la serie de datos o de la función de respuesta (ondícula hija), deben añadirse ceros en un número correspondiente al menos a la mitad del número de valores distintos de cero de la respuesta de frecuencia de la ondícula hija.
Este número depende del escalado y, por tanto, de la frecuencia. Si se añaden ceros para duplicar el tamaño del conjunto de datos, se garantiza que no se produzcan efectos de aliasing en ninguna parte del espectro. A menudo es posible ampliar a la siguiente potencia de 2 y lograr así efectos de aliasing insignificantes, optimizando al mismo tiempo el rendimiento de la FFT.
Si se añaden suficientes ceros, se eliminan los efectos de aliasing, pero se producen otros efectos. Es muy probable que, al añadir los ceros, se cree una discontinuidad al final del flujo de datos. Además, la potencia en los bordes del espectro se reduce insertando ceros en la convolución.
Esta zona con efectos de borde se conoce como "Cone of Influence" (COI). En este rango, en FlexPro no se muestra información espectral. La información espectral del Cone of Influence es probablemente inexacta, independientemente de si se han añadido ceros o no. Si no se han añadido ceros, pueden producirse efectos de aliasing. Si se han añadido ceros, las prestaciones pueden verse reducidas.
El Cone of Influence se calcula como se describe en el artículo de Torrence y Compo.
Ondículas ortogonales y la DWT
La mayoría de los análisis de ondículas utilizan un par de filtros para aislar sucesivamente los componentes de baja y alta frecuencia de una señal. Esto se conoce como transformada discreta de ondículas (DWT = Discrete Ondícula Transform). Las ondículas DWT no son funciones continuas del tiempo y sus transformaciones no son funciones continuas de la frecuencia. En su lugar, son conjuntos de coeficientes de filtro en el dominio del tiempo que generan una base ortogonal que facilita el filtrado y la reconstrucción de los datos. Una DWT no tiene redundancia. El número de bloques de potencias de ondícula para cada escalado es una función del ancho de ondícula no solapado. En una DWT típica, la frecuencia se divide en potencias enteras de dos y el número de bloques por unidad de tiempo también aumenta en potencias de dos con esta frecuencia. Aunque la DFT es rápida y su representación de tiempo-frecuencia requiere poca memoria, no es adecuada para el análisis espectral en el dominio del tiempo y la frecuencia.
FlexPro utiliza exclusivamente la CWT para el análisis espectral en el dominio del tiempo y la frecuencia. El algoritmo CWT ofrece una mayor precisión, pero va acompañado de un elevado esfuerzo de cálculo y altos requisitos de memoria.
Bibliografía
Si quiere saber más sobre los entresijos de la aplicación de la CWT a datos reales, el siguiente artículo es un recurso compacto y fácil de entender:
•Christopher Torrence and Gilbert Compo, "A Practical Guide to Ondícula Analysis", Bulletin of the American Meteorological Society, v. 79, n.º 1, pág. 61-78. Enero de 1998
Esta referencia describe la CWT en el contexto del análisis de las series temporales de El Niño. Los autores también han publicado un programa FORTRAN para el análisis de ondículas llamado WAVEPACK. Está disponible en Internet, en la siguiente dirección: http://paos.colorado.edu/research/wavelets/