Las ventanas de ponderación se utilizan para reducir el manchado espectral en los espectros de Fourier.
Ventanas de ponderación de ancho fijo
Las siguientes ventanas de ponderación de ancho fijo están disponibles en FlexPro. Las ventanas se caracterizan en el dominio de la frecuencia. El valor en dB indica la atenuación del primer lóbulo lateral (Sidelobe) en comparación con el lóbulo principal (Mainlobe). El manchado espectral se reduce al aumentar la atenuación. El término "Rolloff" se refiere al decaimiento de los lóbulos laterales. A medida que aumenta el rolloff, disminuye la dispersión espectral del manchado espectral. El valor W (Width) indica el ancho unilateral del lóbulo principal como múltiplo del ancho del lóbulo principal de la ventana rectangular. La resolución espectral disminuye a medida que aumenta el ancho.
Ventana |
Se calcula con |
|---|---|
Rectángulo -13 dB W=1 (sin ventana de ponderación) |
1.0 |
Welch -21 dB W=1,4 |
1.0-(((n-1)-2*i)/(n-1)*((n-1)-2*i)/(n-1)), i=0..n-1 |
Sine -23 dB W=1,5 |
sin(π*i/(n-1)), i=0..n-1 |
BiSquare -28 dB W=1,8 (Connes) |
1.0-(absolute(i-0.5*n+0.5))²/(0.5*n-0.5)²)², i=0..n-1 |
Bartlett -27 dB W=2 |
2*i/(n-1), i=0..(n-1)/2 2-2*i/(n-1), i=(n-1)/2+1..n-1 |
0.5-0.5*cos(2*π*i/(n-1)), i=0..n-1 |
|
TukeyHann -37 dB W=2 |
0.25*Dirichlet(2*(i/(n-1))-1.0-0.5)+(1.0-2.0*0.25)*Dirichlet(2*(i/(n-1))-1.0)+0.25*Dirichlet(2*(i/(n-1))-1.0+0.5), i=0..n-1 con Dirichlet(q)=sin((2*π+0.5)*q)/(2*π*sin(0.5*q)) |
Bartlett modificado -39 dB W=2,3 |
(sin(π*(2*(i/(n-1))-1)))²/(2*π*sin((i/(n-1))-0.5))², i=0..n-1 |
0.53836-0.46164*cos(2*π*i/(n-1)), i=0..n-1 |
|
Cos3 Maximum Rolloff -47 dB W=3 |
0.375-0.5*cos(2*π*i/(n-1))+0.125*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman -58 dB W=3 |
0.42-0.5*cos(2*π*i/(n-1))+0.08*cos(4*π*i/(n-1)), i=0..n-1 |
0.44959-0.49364*cos(2*π*i/(n-1))+0.05677*cos(4*π*i/(n-1)), i=0..n-1 |
|
Cos3 Nutall -64 dB W=3 |
0.40897-0.5*cos(2*π*i/(n-1))+0.09103*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman Exact -68 dB W=3 |
0.42659071367153912296-0.49656061908856405847*cos(2*π*i/(n-1))+0.076848667239896818573*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman-Harris -68 dB W=3 |
0.42323-0.49755*cos(2*π*i/(n-1))+0.07922*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Minimum Sidelobe -71 dB W=3 |
0.4243801-0.4973406*cos(2*π*i/(n-1))+0.0782793*cos(4*π*i/(n-1)), i=0..n-1 |
Cos4 Maximum Rolloff -61 dB W=4 |
0.3125-0.46875*cos(2*π*i/(n-1))+0.1875*cos(4*π*i/(n-1))-0.03125*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -74 dB W=4 |
0.40217-0.49703*cos(2*π*i/(n-1))+0.09892*cos(4*π*i/(n-1))-0.00188*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -83 dB W=4 |
0.338946-0.481973*cos(2*π*i/(n-1))+0.161054*cos(4*π*i/(n-1))-0.018027*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -92 dB W=4 |
0.35875-0.48829*cos(2*π*i/(n-1))+0.14128*cos(4*π*i/(n-1))-0.01168*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -93 dB W=4 |
0.355768-0.487396*cos(2*π*i/(n-1))+0.144232*cos(4*π*i/(n-1))-0.012604*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -96 dB W=4 |
0.3635819-0.4891775*cos(2*π*i/(n-1))+0.1365995*cos(4*π*i/(n-1))-0.0106411*cos(6*π*i/(n-1)), i=0..n-1 |
1-1.93*cos(2*π*i/(n-1))+1.29*cos(4*π*i/(n-1))-0.388*cos(6*π*i/(n-1))+0.0322*cos(8*π*i/(n-1)), i=0..n-1 |
Ventanas de ponderación de ancho variable
Las siguientes ventanas de ponderación con ancho ajustable están disponibles en FlexPro:
Ventana |
Se calcula con |
|---|---|
Beta |
4*(1-i/(n-1))*i/(n-1))^(-3.218913776512187+2.760793796409310*a), i=0..n-1 a=ancho del lóbulo principal |
Coseno Maximum Rolloff |
absolute(0.5*(1-cos(2*π*i/(n-1)))))^(a-1), i=0..n-1 Es la ventana de coseno con máximo decaimiento de los lóbulos laterales. |
Kaiser-Bessel |
I0(sqrt((a²-1.0)/0.10132118361)*sqrt(i*(2*((n-1)/2)-i))/((n-1)/2))/I0(sqrt((a²-1.0)/0.10132118361)), i=0..n-1 a=ancho del lóbulo principal, I0 es la función de Bessel modificada |
van der Maas |
0.5*I1(2*(0.5*π*sqrt(4*a*a-1))*sqrt((i/(n-1))*(1-(i/(n-1)))))/(sqrt((i/(n-1))*(1-(i/(n-1))))*I1(0.5*π*sqrt(4*a*a-1))), i=0..n-1 a=ancho del lóbulo principal, I1 es la función de Bessel modificada |
Esta ventana produce un manchado espectral mínimo debido a los lóbulos laterales, pero no tiene "Rolloff". Se construye en el dominio de la frecuencia y se transforma inversamente para su uso en el dominio del tiempo. FlexPro implementa la ventana de Chebyshev en el rango de -30 dB a -150 dB.
Véase también el programa 5.2 de "IEEE Programs for Digital Signal Processing" |
|
Chebyshev (aproximado) |
Se trata de una aproximación de la ventana de Chebyshev utilizada en FlexPro con un rango de validez de -50 a -130 dB. Se utiliza principalmente en el objeto de análisis Análisis de Fourier para datos muestreados no equidistantes. |
Slepian (DPSS) |
Es la primera ventana de la serie Slepian DPSS. El parámetro a corresponde aproximadamente al ancho del lóbulo principal.
Véase también Jonathan Lees und Jeffrey Park, "Multiple Taper Spectral Analysis". |
Gaussiano |
exp(-4*ln(2)*((i-((n-1)/2))/((n-1)*((2.453274901281656+a*0.3202556336455866)/(1.0+a*(2.348619671799226))))²), i=0..n-1 a=ancho del lóbulo principal |
Cosine Taper |
if(i>(int)(a*n+0.5) and i<(int)((1.0-a)*n-0.5)), 1.0, 0.5-0.5*cos((π/a/(n-1))*(if(i>0.5*n, n-i-1, i)))), i=0..n-1 La ventana varía de Hann en a=0,5 hasta un rectángulo de a contra 0. |
Los siguientes gráficos muestran una serie de ventanas de las más populares:
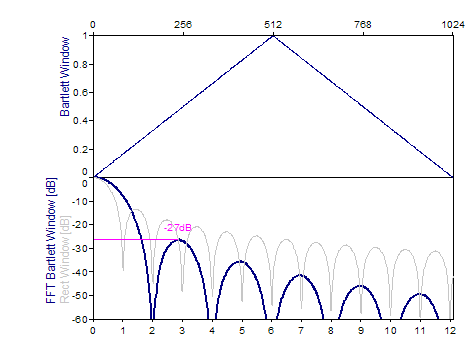
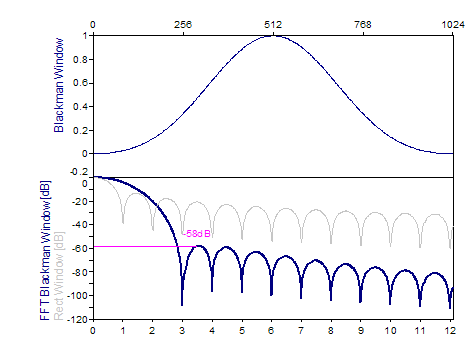
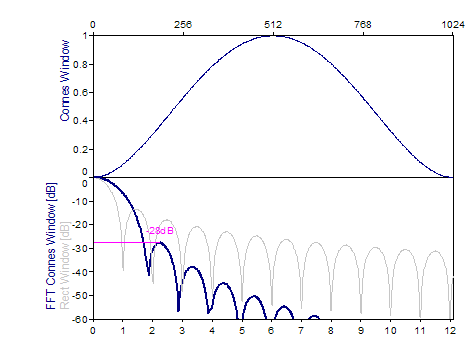
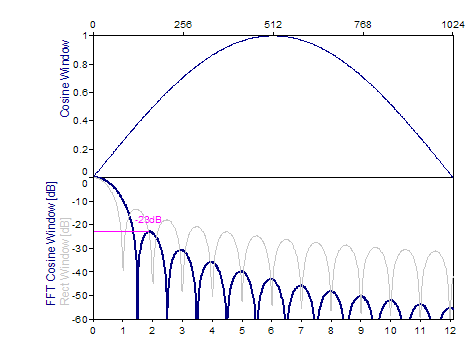
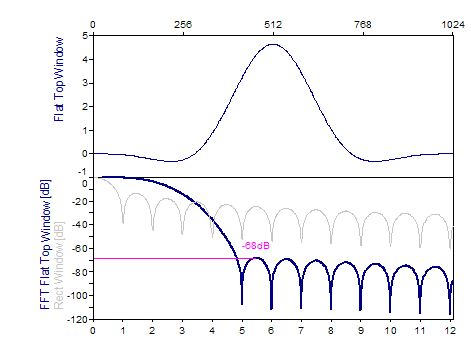
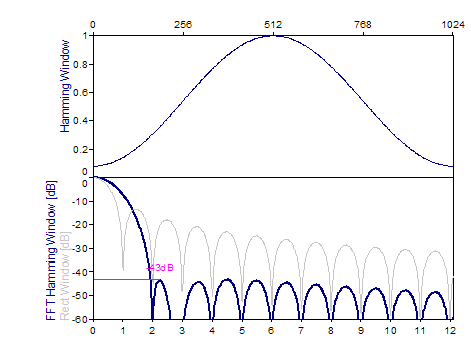
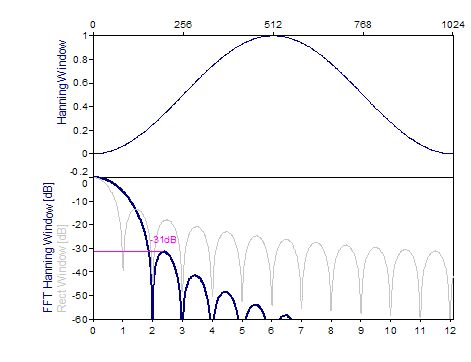
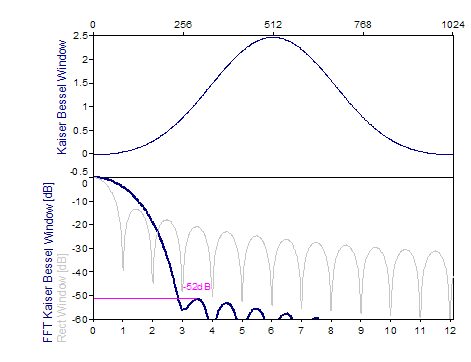
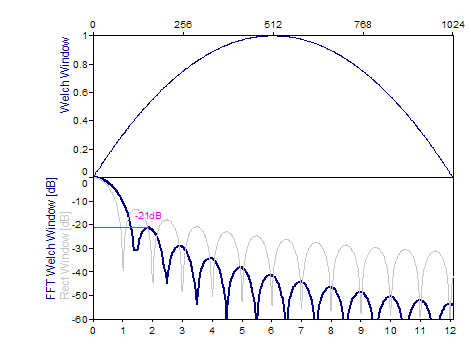
Bibliografía
Una implementación de la ventana de Chebyshev se describe en:
•IEEE Programmes for Digital Signal Processing, IEEE Press, 1979.
La ventana Slepian (DPSS) se presenta en:
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, pág. 199, 1995.
Aquí se ofrece una visión general de las distintas ventanas:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behaviour", IEEE Trans. ASSP, v29-1 de febrero de 1981.