Definición de amplitud instantánea, fase instantánea y frecuencia instantánea
Al transformar la señal de entrada real en una señal analítica, se pueden derivar y analizar las características locales de la señal original, la amplitud instantánea, la fase instantánea y la frecuencia instantánea:
Para ello, escriba la señal analítica z(t) en representación polar de la siguiente manera:
La amplitud instantánea (en bibliografía inglesa como Instantaneous Amplitude o Instantaneous Envelope) se define ahora como la amplitud a(t) de la señal analítica, es decir:
Si la señal original no tiene tendencia ni offset, proporciona la evolución de la amplitud o la envolvente superior de la señal que se va a analizar.
La fase instantánea (en bibliografía inglesa como Instantaneous Phase) es la fase de la señal analítica Φ(t). La fase Φ(t) puede modelarse de la siguiente forma:
La frecuencia instantánea ω(t) (en bibliografía inglesa como Instantaneous Frequency) se define finalmente como:
Para las señales de un solo componente sin tendencia ni offset, estas definiciones proporcionan la evolución de la fase y de la frecuencia de la señal que se va a analizar.
Para las señales que tienen una tendencia o un offset, todas las interpretaciones anteriores solo son correctas si se produce una corrección de tendencia de la señal. El siguiente ejemplo ilustra estas relaciones.
Para más detalles, véase también [2] y [3].
Aplicaciones: Cálculo de la amplitud instantánea, la fase instantánea, la frecuencia instantánea y la envolvente
Nota preliminar: Las siguientes fórmulas FPScript para calcular la amplitud instantánea, la fase instantánea y la frecuencia instantánea forman la base del objeto de análisis Magnitud instantánea. Por lo tanto, el siguiente ejemplo puede calcularse de forma analógica con el objeto de análisis Magnitud instantánea.
Para el ejemplo de demostración, cree primero un coseno de frecuencia variable con 10000 valores, cuya componente X tenga la unidad s, empiece en 0 s y termine en 20 s. La frecuencia inicial es de 5 Hz y la final de 15 Hz. La amplitud del coseno de frecuencia variable es 1, el offset y la fase de inicio son ambos 0. Ahora escale la señal sintética generada mediante la siguiente fórmula (llamada Data):
Dim amplitude = Sqrt(Value Signal.X + 1)
amplitude * Signal
Se proporciona el espectro de tiempo-frecuencia de la señal escalada (visualizado en un diagrama de contorno 3D):
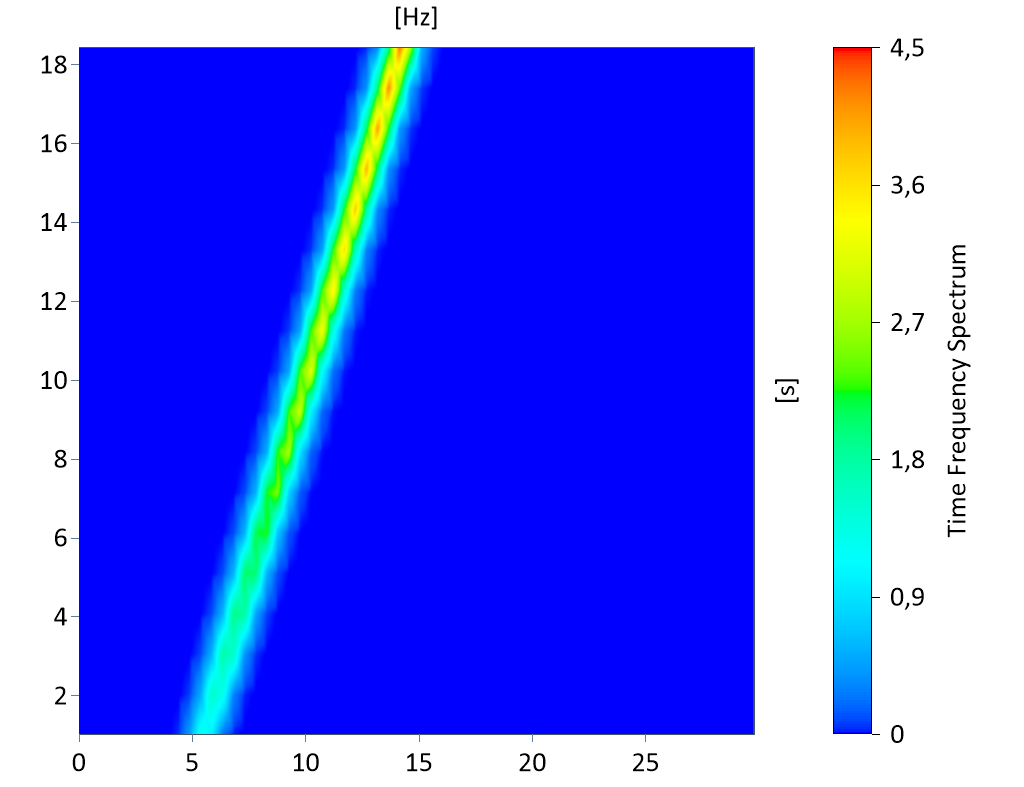
La señal no tiene tendencia. Por lo tanto, la amplitud instantánea se calcula ahora de la siguiente forma:
Absolute(AnalyticSignal(Data))
Como se ha indicado anteriormente, esto corresponde ahora a la envolvente superior (o la evolución de la amplitud) de la señal escalada:
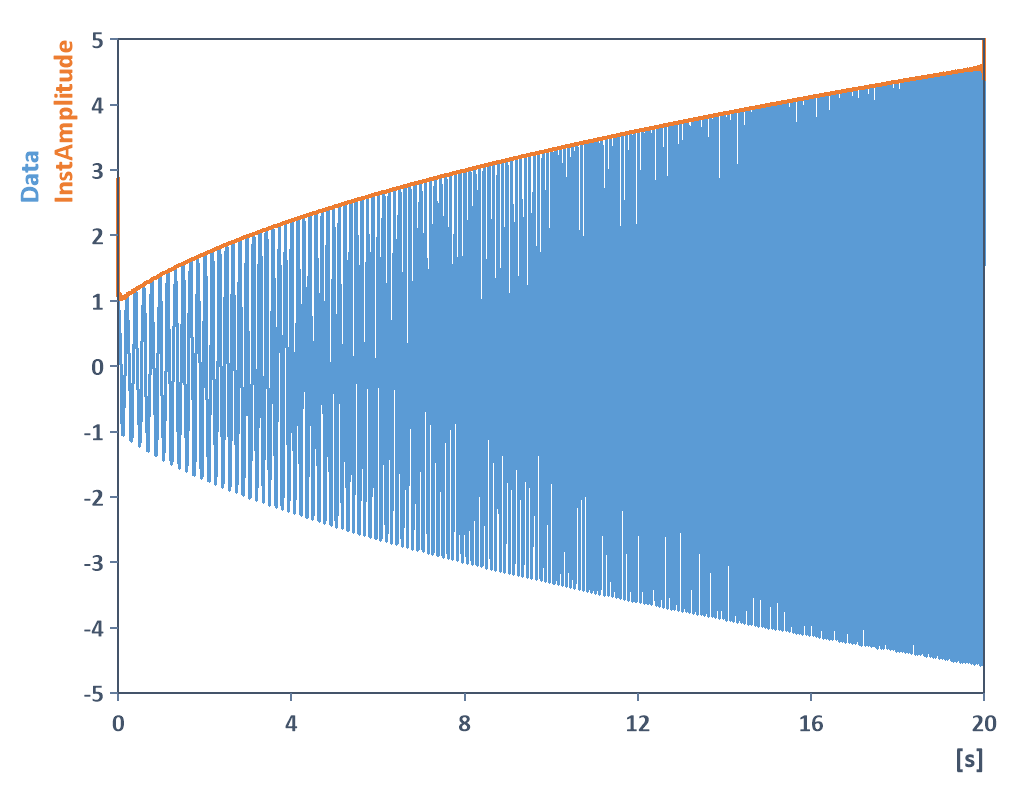
Puede obtener la envolvente inferior del mismo modo utilizando
-Absolute(AnalyticSignal(Data))
Uitlice ahora el siguiente código FPScript para calcular la frecuencia instantánea:
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(Data)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
Esto proporciona la evolución de la frecuencia de la señal:
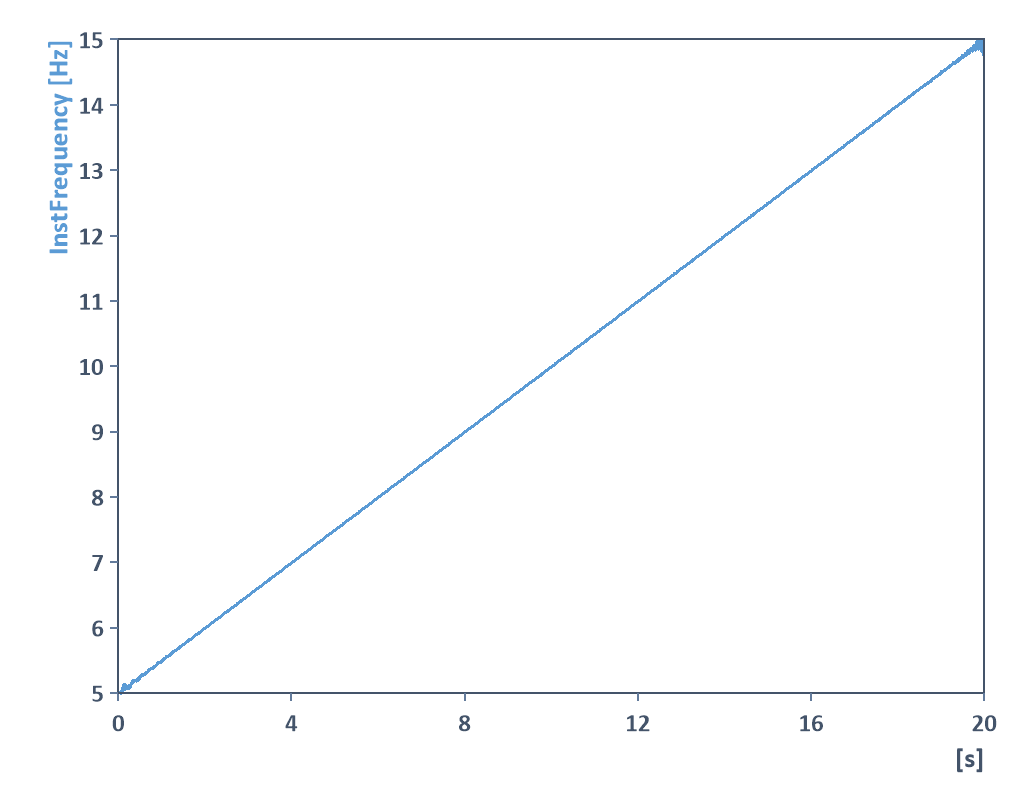
Cree ahora una segunda fórmula (llamada DataWithOffset) en la que se añade un offset o tendencia.
Por ejemplo: Data + 35
Nota Tenga en cuenta que para determinar la evolución de la amplitud, la fase, la frecuencia o la envolvente (utilizando los algoritmos anteriores), es necesario aplicar una corrección de tendencia o de offset a la señal que se va a analizar.
Primero se calcula de nuevo la amplitud instantánea. La corrección de la tendencia puede realizarse generalmente con la función FPScript Trend o mediante medias móviles utilizando la función Mean, por ejemplo:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset))
Esto proporciona ahora la evolución de amplitud de la señal escalada con un offset. Sin embargo, para determinar la envolvente, hay que volver a sumar la tendencia. Por tanto, la fórmula debe modificarse ligeramente de la siguiente forma:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Absolute(AnalyticSignal(DataWithOffset - offset)) + offset
Proporciona la envolvente superior de la señal escalada con un offset:
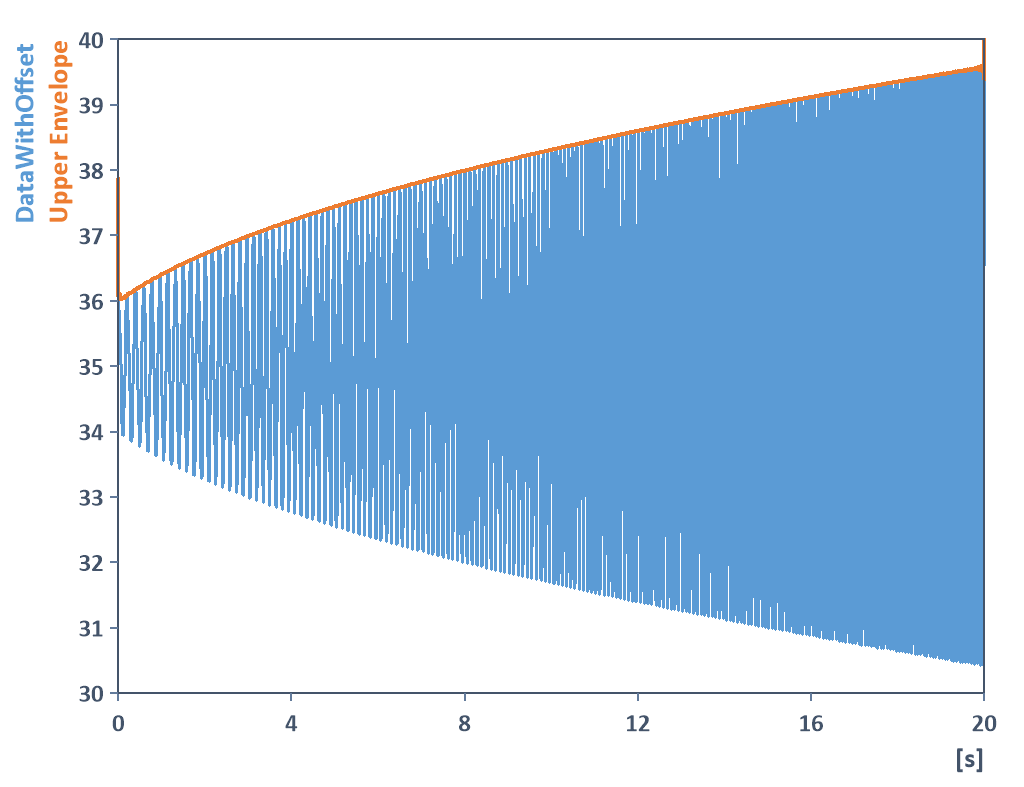
Tenga en cuenta que el offset debe sustraerse de la misma manera para determinar la evolución de la frecuencia:
Dim offset = Trend(DataWithOffset, TREND_CONSTANT)
Dim instPhase = PhaseUnwrap(Phase(AnalyticSignal(DataWithOffset - offset)))
ChangeUnit(1/(2*PI)*Derivative(instPhase), "Hz")
Nota 1: Al calcular la amplitud instantánea, la fase instantánea, la frecuencia instantánea o la envolvente, pueden producirse efectos secundarios en forma de sobreoscilaciones en los bordes de la señal (o más generalmente en las proximidades de las discontinuidades de la señal). Estas sobreoscilaciones no pueden evitarse en el algoritmo anterior y son puramente matemáticos. Esto se debe al fenómeno de Gibbs, que provoca sobreoscilaciones en las proximidades de las discontinuidades en las series de Fourier y las transformadas de Fourier.
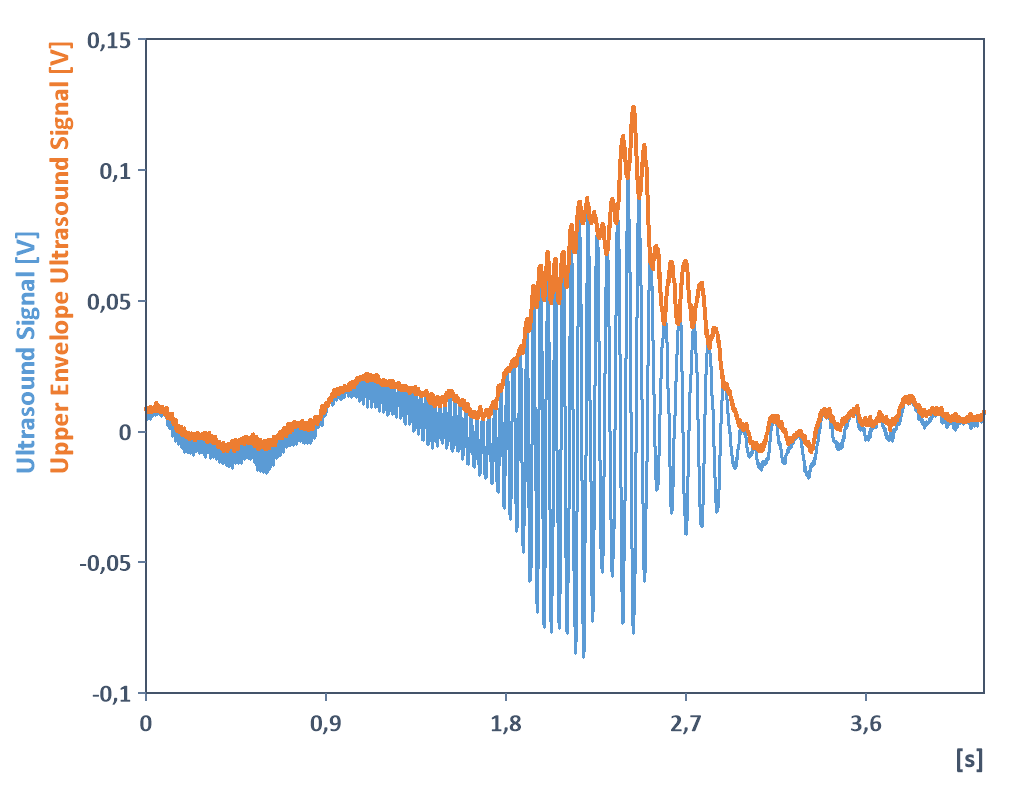
Nota 2: En la siguiente señal proporcionada con los datos de ejemplo de FlexPro, el algoritmo anterior para calcular la envolvente superior (aplicando una corrección de tendencia utilizando la función Mean) realmente proporciona, como era de esperar, la envolvente superior. La señal no tiene que ser monocomponente:
Nota 3: Debe tenerse en cuenta que, en el caso de señales multicomponentes, las interpretaciones como fase instantánea y frecuencia instantánea ya no son válidas. Considere el siguiente código FPScript:
Dim x = Series(0 s, 1 s, 0.001)
Dim y = Sin(2 * PI * x * 30 Hz) + Sin(2 * PI * x * 90 Hz)
Señal (y,x)
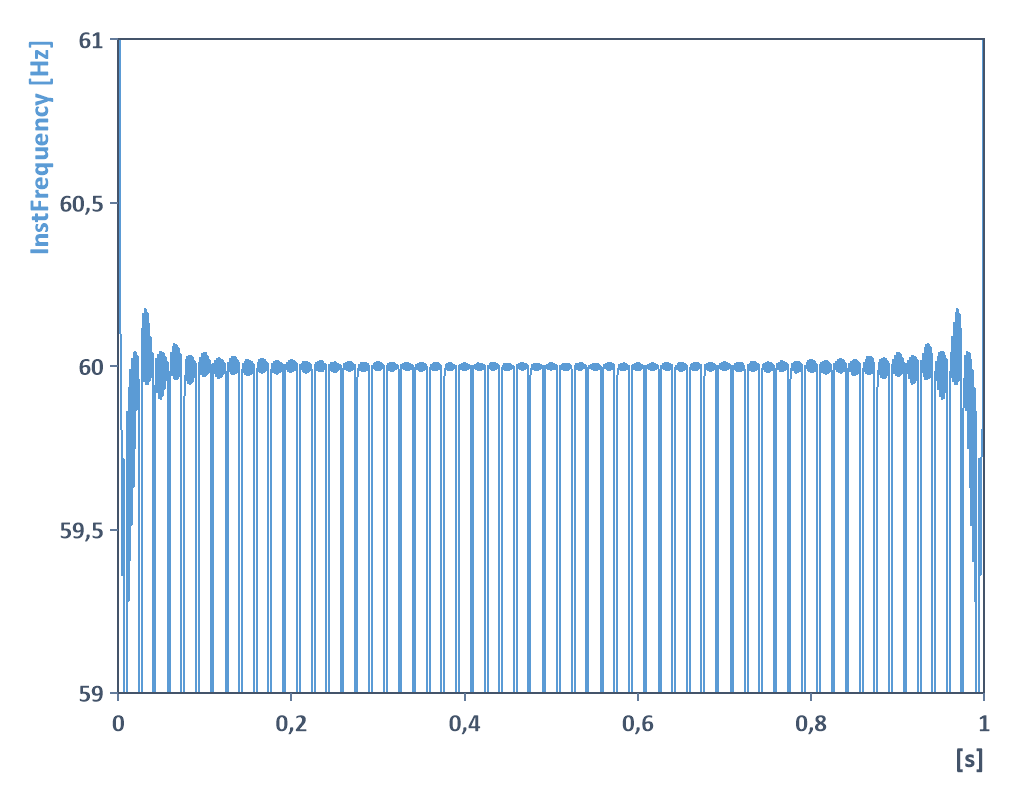
En este caso, el algoritmo para determinar la frecuencia instantánea proporciona una media de las dos frecuencias senoidales:
Más aplicaciones: Demodulación de señales (demodulación de amplitud, demodulación de fase, demodulación de frecuencia)
Los valores instantáneos así definidos también pueden utilizarse para demodular señales. Dada, por ejemplo, una señal modulada de la forma:
La amplitud instantánea proporciona, de hecho, la evolución de amplitud a(t), mientras que la fase instantánea se calcula como Φ(t). La frecuencia instantánea también puede utilizarse para determinar la evolución de frecuencia de la señal especificada.
Antecedentes teóricos: Algoritmo de cálculo de la señal analítica
La regla de cálculo en tiempo continuo dada anteriormente define la función de transferencia H en el dominio de la frecuencia. Por lo tanto, el algoritmo para calcular la señal analítica discreta se realiza utilizando la FFT y la función de transferencia discreta H como se describe a continuación, véase en particular [1]:
La función de transferencia se da para longitudes de la FFT pares como: H[k] = 2 para k = 1, 2, ..., FFTLength/2 - 1 (corresponde a las frecuencias positivas) y H[k] = 0 para k = FFTLength/2 + 1, ..., FFTLength (corresponde a las frecuencias negativas). Los coeficientes simétricos k = 0 y k = FFTLength/2 tienen una posición especial. Para estos, H[k] = 1.
La función de transferencia para longitudes de la FFT impares se da analógicamente como: H[k] = 2 para k = 1, 2, ..., (FFTLength-1)/2 y H[k] = 0 para k = (FFTLength-1)/2 + 1, ..., FFTLength y también H[0] = 1.
Por lo tanto, el algoritmo FPScript para calcular la señal analítica se define de la siguiente manera (el argumento FFTLength debe ser mayor o igual a la longitud de datos):
Arguments sig, FFTLength
Dim N = NumberOfRows(sig)
Dim fftInput = ComplexFloatingPoint64(sig.Y : (0 # (FFTLength - N)))
Dim fourierTrafo = FFTn(fftInput)
Dim H = 0 # FFTLength
H[0] = 1
If FFTLength Mod 2 == 0 Then
H[FFTLength/2] = 1
H[1, FFTLength/2 - 1] = 2
Else
H[1, (FFTLength - 1)/2] = 2
End
return Signal(IFFTn(H * fourierTrafo)[0, N-1], sig.X)
Efecto de la longitud de la FFT: La resolución de la FFT necesaria para el algoritmo se aumenta mediante el relleno de ceros (Zero-Padding), es decir, seleccionando una longitud de la FFT mayor que la longitud de los datos. Esto puede mejorar el resultado del cálculo. Puede encontrar un ejemplo en la ayuda en línea de la función Hilbert.
Bibliografía
[1] S. Lawrence Marple, Jr., "Computing the Discrete-Time "Analytic" Signal via FFT", IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222,1999.
[2] B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono, "On Instantaneous Amplitude and Phase of Signals", IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833,1997.
Véase también
Objeto de análisis Magnitud instantánea