Tutorial Filtros digitales

Este tutorial cubre tanto el diseño del filtro FIR como el diseño del filtro IIR en FlexPro.

Señal de ejemplo

Generamos una señal sintética con el objeto de análisis Señal, lo que nos permite demostrar muy bien las propiedades del filtro. Seleccione Insertar[Datos] > Señal > Coseno de frecuencia variable. Configure la función coseno de frecuencia variable con la Frecuencia 1 y la 2.ª frecuencia 10000. En la pestaña Muestreo, determine el componente X con un Valor inicial de 0, un Valor final de 0,5 y un Número de valores de 10000.

Filtro IIR

Seleccione el conjunto de datos Signal.

Haga clic en Insertar[Análisis] > Asistente para análisis.

Seleccione la categoría Filtros IIR en Filtros. Seleccione allí Filtro IIR. Pulse el botón Siguiente.

El paso 2 del asistente para análisis contiene un diálogo interactivo en el que se pueden seleccionar distintos tipos y características del filtro. En la ventana de vista previa del asistente para análisis aparecen tres diagramas. Puede ver la señal de entrada, la especificación del filtro y la señal filtrada, o un diagrama con los coeficientes del filtro. La opción Mostrar respuesta de amplitud permite mostrar u ocultar la respuesta de amplitud en el diagrama con la especificación del filtro. La respuesta de amplitud también se muestra en forma logarítmica.

Seleccione Paso alto como Tipo de filtro y Chebyshev como Característica del filtro. Este filtro puede utilizarse para influir en la ondulación de la banda de paso. Active la opción Utilizar frecuencias normalizadas. Seleccione el Orden 7 como especificación del filtro, la frecuencia de corte normalizada Fc1 0,25 y el valor 0,2 como Error en la banda de paso. Si observamos ahora la especificación del filtro generado, veremos que la ondulación del filtro en la banda de paso oscila entre 0,8 y 1, es decir, que tiene un error máximo de 0,2. Si se reduce la ondulación, se hace a expensas de la pendiente del filtro en la banda de transición.

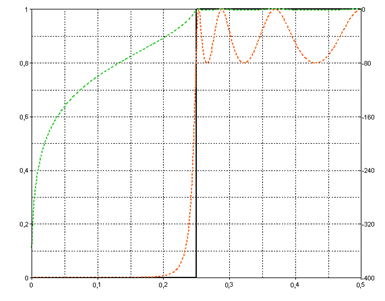
A diferencia del filtro Chebyshev, para el filtro Chebyshev inverso se puede especificar la ondulación en la banda de rechazo. El diseño del filtro Cauer es aún más flexible, ya que se puede definir la ondulación tanto en la banda de paso como en la banda de rechazo.

Se puede especificar un orden del filtro fijo para los filtros IIR. También es posible calcular el orden del filtro en relación con la especificación dada. En lugar de la frecuencia de corte normalizada, se especifica un límite inferior y uno superior para cada banda de transición. Además, se especifican tanto el error en la banda de paso como el error en la banda de rechazo. Según la especificación, la señal filtrada no debe caer por debajo ni superar estos errores en los límites de banda definidos.

Seleccione Calcular como Orden y las frecuencias normalizadas 0,24 y 0,26 y como Transición. Introduzca 0,1 para ambos Errores. En lugar del error, también puede especificar la ondulación en la banda de paso o la atenuación en la banda de rechazo en decibelios. Si cambia el Modo, los valores se convierten en consecuencia.

Opciones de salida del asistente para análisis

Para ver los objetos que genera el asistente para análisis automáticamente, haga clic en Siguiente. En el paso 3, seleccione las dos opciones activas y haga clic en Finalizar.

Se crearon siete objetos en la base de datos del proyecto FlexPro.

FiltroIIR es el objeto de análisis. Realiza el filtrado. Puede abrir el objeto haciendo doble clic sobre él.

La Especificación es la fórmula para generar la especificación que se utiliza en la presentación.

La Respuesta de amplitud es la fórmula para generar la respuesta de amplitud del filtro, que también se utiliza en la presentación.

El diagrama Señal contiene la señal de entrada, el diagrama Filtro IIR muestra la señal filtrada o los coeficientes del filtro y el diagrama Especificación muestra la especificación del filtro.

El documento Filtro IIR contiene los tres diagramas generados.

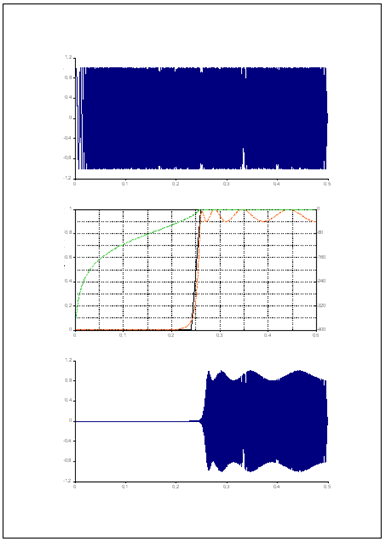
El orden de los filtros IIR se limita a 10, ya que a órdenes superiores se producen inestabilidades. Por lo tanto, veamos ahora el diseño del filtro FIR, que permite órdenes más altos y también es más flexible que el diseño del filtro IIR.

Filtro FIR

A diferencia del diseño del filtro IIR, existen dos métodos de cálculo diferentes para el diseño del filtro FIR: el diseño del filtro mediante ventanas y el algoritmo FIR Equiripple (método Parks-McClellan).

Diseño del filtro FIR mediante ponderación de ventana

Volvemos a utilizar la señal sintética. Seleccione el conjunto de datos Signal.

Haga clic en Insertar[Análisis] > Asistente para análisis.

Seleccione la categoría Filtros FIR en Filtros. Seleccione allí Método de ventana. Pulse el botón Siguiente. Seleccione Señal filtrada como Resultado y Pasa banda como Tipo de filtro. Active la opción Utilizar frecuencias normalizadas. Utilice la Ventana de Hamming con las frecuencias de corte Fc1 igual a 0,1 y Fc2 igual a 0,4 y una Longitud del filtro de 71. Haga clic en el botón Finalizar. Si ahora selecciona la señal de entrada y el objeto de filtro que acaba de crear y crea un diagrama de líneas, detectará un desplazamiento de fase entre las dos señales. Puede eliminar este desplazamiento de fase seleccionando Señal filtrada con corrección de fase como resultado en la segunda página del asistente. Los filtros FIR tienen un desplazamiento de fase constante que solo depende de la longitud del filtro y de la frecuencia de muestreo de la señal. La corrección de fase también es posible en el diseño del filtro IIR. Sin embargo, ahí la corrección de fase se realiza filtrando la señal dos veces, una desde delante y otra desde atrás.

Seleccione de nuevo la señal y vuelva al asistente para diseñar el filtro mediante ventana. Los distintos tipos de ventanas tienen un comportamiento de atenuación diferente. Si la opción Mostrar respuesta de amplitud está activada, la atenuación de rechazo se muestra en el diagrama con la especificación en forma de línea horizontal, a excepción de la ventana Hamming generalizada. Para las ventanas rectangular, Bartlett, Hamming, Hanning y Blackman, la atenuación es fija (método de ventana). En el caso de la ventana Hamming generalizada, la atenuación de rechazo puede verse influida por el parámetro alpha, que puede oscilar entre 0 y 1. Las dos ventanas más flexibles son las de Kaiser y Chebyshev, ya que el tercer parámetro puede calcularse a partir de dos de los tres parámetros: longitud del filtro, atenuación y transición.

En la segunda página del asistente, seleccione como resultado Coeficientes del filtro. En el diagrama inferior, ahora se muestra la respuesta al impulso (correspondiente a los coeficientes del filtro) en lugar de la señal filtrada. Para generar un pasa banda, seleccione la ventana Kaiser con las frecuencias de corte Fc1 igual a 0,1 y Fc2 igual a 0,4. En Cálculo de, seleccione Longitud del filtro. Especifique un filtro con una Atenuación de 20 dB y una Transición de 0,01. Con este método conseguimos una Longitud del filtro de 94.

Ahora queremos diseñar un filtro con las características del filtro que acabamos de describir utilizando el método FIR Equiripple, para poder comparar los dos procedimientos para el diseño del filtro FIR.

Diseño del filtro FIR mediante el método Equiripple

En el asistente para análisis, seleccione la categoría Filtros FIR en Filtros. Allí, seleccione Método Equiripple. Pulse el botón Siguiente.

Ahora seleccione Coeficientes del filtro como Resultado, Pasa banda como Plantilla de filtro y Calcular como Longitud del filtro. Active la opción Utilizar frecuencias normalizadas. Se predefinen tres bandas para un pasa banda en la lista de bandas. Para cada banda pueden introducirse los límites inferior y superior, los factores ganancia correspondientes y el error de aproximación o la ponderación. La transición entre una banda de rechazo y una de paso está formada por la diferencia entre el límite superior de una banda y el límite inferior de la banda siguiente. Puede editar los valores individuales haciendo doble clic en las entradas de la lista. Sin embargo, algunas entradas, como los factores ganancia, están bloqueadas para las plantillas de filtro predefinidas. Introduzca ahora los siguientes valores en la lista:

Se requiere una longitud del filtro de 77 para este filtro utilizando el método FIR Equiripple. Tanto la banda de paso como la de bloqueo tienen una ondulación uniforme. Por ello, estos filtros también se denominan filtros Equiripple. En el diseño del filtro IIR, es posible conseguir una ondulación uniforme en las bandas de paso y de rechazo con ayuda del filtro Cauer. Sin embargo, ahí la ondulación no está en el rango de 1±δ, sino entre 1-δ y 1.

El método FIR Equiripple puede utilizarse para diseñar filtros óptimos en relación con la especificación. El resultado son filtros con una longitud del filtro más corta que cuando se diseñan filtros utilizando ventanas. El método FIR Equiripple también tiene la ventaja de que se pueden diseñar filtros multibanda.

Diseño de un filtro multibanda

Para el diseño del filtro multibanda se utiliza una señal que contiene cuatro curvas senoidales con la misma potencia, que se extienden por el rango de Nyquist, y tres curvas senoidales con menor potencia, que se sitúan entre ambas. Los componentes de baja potencia están -40 dB, -50 dB y -60 dB por debajo de las curvas senoidales de referencia. Además, se añade ruido blanco para que el ruido de fondo sea de aproximadamente -75 dB.

Las siete curvas senoidales tienen este aspecto:

1.0*sin(2π*x*1005+π/2)+ (0 dB)

1.0*sin(2π*x*2005+π/2)+ (0 dB)

1.0*sin(2π*x*3005+π/2)+ (0 dB)

1.0*sin(2π*x*4005+π/2)+ (0 dB)

0.01*sin(2π*x*1505+π/2)+ (-40 dB)

0.003162*sin(2π*x*2505+3π/2)+ (-50 dB)

0.001*sin(2π*x*3505+π) (-60 dB)

El valor X (tiempo) varía de 0 a 0,1 con un incremento de 0,0001. La frecuencia de Nyquist es, por tanto, 5000 (la mitad de la frecuencia de muestreo de 10000). Las cuatro curvas senoidales de referencia se extienden por el rango de Nyquist. La primera curva senoidal de baja potencia (-40 dB) tiene el 1 % de la amplitud de las curvas senoidales de referencia y el 0,01 % de la potencia de una de las curvas senoidales de referencia. La segunda curva senoidal de baja potencia (-50 dB) tiene el 0,001 % de la potencia de las curvas de referencia. La última curva de prueba (-60 dB) solo tiene el 0,1 % de la amplitud y el 0,0001 % de la potencia de las curvas de referencia. Se añadió ruido gaussiano (al 0,15 %) para crear un ruido de fondo de aproximadamente -75 dB. Esta señal también se puede encontrar en el tutorial Análisis espectral.

Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Filter.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples>Tutorials>Filter.fpd. Seleccione el conjunto de datos Signal2. Haga clic en Insertar[Análisis] > Asistente para análisis. Seleccione la categoría Filtros FIR en Filtros. Allí se selecciona el Método Equiripple. Pulse el botón Siguiente.

Ahora diseñaremos un filtro multibanda que filtre todos los componentes de la señal excepto las curvas senoidales a 1000 y 3000 Hz. Para ello, seleccione Señal filtrada con corrección de fase como Resultado y Multibanda como Plantilla de filtro. Active la opción Utilizar frecuencias normalizadas. Seleccione Calcular como Longitud del filtro. Añada bandas a la lista hasta que haya un total de 5 bandas disponibles. Introduzca ahora los siguientes valores en la lista:

Ahora puede guardar estas entradas como plantilla de filtro para utilizarlas más adelante. Para ello, introduzca el nombre Multi1 en Plantilla de filtro y pulse el botón Guardar. Si posteriormente realiza otro cambio en la lista, deberá guardarlo de nuevo. Haga clic en el botón Finalizar. FlexPro guarda las plantillas en su perfil de usuario.

Ahora puede comprobar el resultado con una simple FFT. Además, la opción Análisis espectral le ofrece aún más opciones de análisis, como la creación de una función de transferencia a partir de la señal de entrada y la señal filtrada.

Diseño del filtro basado en una respuesta de amplitud predefinida

Al final del tutorial, utilizaremos el método FIR Equiripple para diseñar un filtro en el que los factores ganancia o la respuesta de amplitud se especifican como un conjunto de datos. Seleccione el conjunto de datos Signal. Abra de nuevo el asistente para análisis y seleccione el método FIR Equiripple. A continuación, realice la siguiente configuración: Plantilla de filtro (personalizada), Calcular longitud del filtro, Ponderación de lista. Active la opción Utilizar frecuencias normalizadas. Defina las siguientes bandas:

Seleccione ahora el conjunto de datos Amplitud como factor ganancia. Este conjunto de datos es la respuesta de amplitud generada a partir de un elimina banda IIR (filtro Cauer). Si ahora observa la especificación, verá que la especificación del filtro ya no está definida por constantes en las bandas de paso y de rechazo, sino por el conjunto de datos especificado.

 

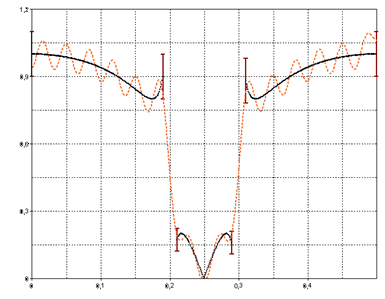
También es posible definir una sola banda en todo el dominio de la frecuencia normalizada de 0 a 0,5. Sin embargo, debe asegurarse de que las bandas individuales no presentan discontinuidades, ya que de lo contrario el algoritmo no convergerá. En principio, puede decirse que el diseño del filtro basado en una respuesta de amplitud predefinida es muy intensivo desde el punto de vista del cálculo, si hay que calcular la longitud del filtro. Además, el algoritmo no converge muy bien, en función de la especificación predefinida. En ese caso, hay que aumentar los errores de aproximación o modificar las frecuencias de corte de las bandas.

Si la longitud del filtro es fija, las ponderaciones de las bandas también pueden especificarse utilizando un conjunto de datos.

Filtrado de varias señales de entrada

También tiene la opción de filtrar varias señales al mismo tiempo mediante el asistente para análisis. Para ello, seleccione las señales que desea filtrar, abra el asistente para análisis y seleccione como resultado Señal filtrada o Señal filtrada con corrección de fase. El asistente para análisis crea un objeto de análisis que calcula los coeficientes del filtro. Además, se crea una fórmula FPScript para cada señal de entrada, que filtra la señal de entrada utilizando los coeficientes del filtro calculados.

Comparación de filtros IIR y FIR

En este tutorial se presentan varios métodos de diseño de filtros IIR y FIR. Naturalmente, se plantea la cuestión de si son preferibles los filtros IIR o los FIR. Ambos tipos de filtro tienen ventajas e inconvenientes. Por lo tanto, no hay una respuesta clara a esta pregunta. He aquí algunos puntos que le ayudarán a tomar una decisión:

Filtro IIR

Ventajas:

•Cálculo sencillo, ya que muchos filtros selectivos en frecuencia pueden calcularse con fórmulas de diseño cerradas

•La especificación de la respuesta de amplitud con los filtros IIR presenta la máxima eficacia

•Retardo de grupo inferior al de los filtros FIR

•Se necesita menos longitud del filtro

Desventajas:

•Sin fase lineal

•Retardo de grupo variable

•Solo son estables si todas las posiciones de los polos se encuentran dentro del círculo unitario

Filtro FIR

Ventajas:

•Es posible diseñar filtros con fase lineal

•Son siempre estables (solo contienen ceros en la función de transferencia)

•Retardo de grupo constante

Desventajas:

•Se necesitan procedimientos iterativos complejos

•Se necesitan muchos coeficientes para realizar filtros con alta pendiente (se requiere un orden del filtro mayor que con los filtros IIR)

El método FIR Equiripple conduce a filtros de menor orden que el método de ventana y ofrece más opciones de diseño (ponderación, error de aproximación) en la especificación del filtro. El método FIR Equiripple también puede utilizarse para diseñar filtros multibanda.

Bibliografía

Estas son algunas introducciones recomendables al filtrado digital:

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, Nueva York.

Aquí se describen los algoritmos de filtrado utilizados en FlexPro:

•J.H. McClellan, T.W. Parks, L.R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, N.º 6, diciembre de 1973

•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, N.º. 4, pág. 595 610, abril de 1975

•L. R. Rabiner, C. A. McGonegal and D. Paul (1979). FIR Windowed Filter Design Program - WINDOW. Section 5.2 in Programs for Digital Signal Processing, IEEE Press, pág. 5.2-1 a 5.2-19.

Véase también

Opción Filtros digitales

Asistente para análisis

Objeto de análisis Filtro FIR (método de ventana)

Objeto de análisis Filtro FIR (método Equiripple)

Objeto de análisis Filtro IIR

Método de ventana

Método FIR Equiripple