Este tutorial cubre los procedimientos espectrales en FlexPro en los que se analiza la similitud de dos señales. El espectro cruzado, el periodograma cruzado y las funciones de coherencia ofrecen posibilidades para evaluar la similitud o disimilitud de dos señales. Estos métodos suelen utilizarse para señales que proceden de la misma fuente. Sin embargo, no necesariamente es así. Se pueden utilizar dos señales cualesquiera de la misma longitud del conjunto de datos.
Este tutorial también cubre las funciones de transferencia de Fourier entre una señal de entrada y una de salida.
Análisis de Fourier
Si todavía no ha completado el tutorial Análisis espectral de Fourier, debería hacerlo antes de empezar con este. En él se describen la mayoría de los principios del análisis de Fourier. Este tutorial trata principalmente de las particularidades que deben observarse al analizar dos señales mediante el análisis espectral cruzado.
Dos señales de prueba
Para este tutorial se utilizan dos señales de longitud 1024. La primera señal es la señal de referencia, que contiene nueve curvas senoidales distribuidas uniformemente en el rango de Nyquist:
100.0*sin(2π*x*250+π)
100.0*sin(2π*x*500+π)
100.0*sin(2π*x*750+π)
100.0*sin(2π*x*1000+π)
100.0*sin(2π*x*1250+π)
100.0*sin(2π*x*1500+π)
100.0*sin(2π*x*1750+π)
100.0*sin(2π*x*2000+π)
100.0*sin(2π*x*2250+π)
Para ver los efectos de la modificación de las amplitudes, frecuencias y fases en el análisis espectral cruzado, los componentes de la segunda señal se modifican del siguiente modo:
100.0*sin(2π*x*250+π)
75.0*sin(2π*x*500+π)
50.0*sin(2π*x*750+π)
25.0*sin(2π*x*1000+π)
0.0*sin(2π*x*1250+π)
100.0*sin(2π*x*1502.5+π)
100.0*sin(2π*x*1775+π)
100.0*sin(2π*x*2000+0)
100.0*sin(2π*x*2250+π/2)
Los cinco primeros componentes tienen un descenso lineal de amplitud del 100 % al 0 %. Los dos componentes siguientes se desvían hacia arriba un 0,1 % y un 1 % del rango de Nyquist. Los dos últimos componentes tienen un desfase de -π y -π/2.
La frecuencia de muestreo es de 5000 Hz. Esto significa que la frecuencia de Nyquist, la frecuencia máxima que se puede analizar, es de 2500 Hz. Los valores de tiempo varían de 0 a 0,2045 con un intervalo de muestreo de 0,0002. A ambas señales se les ha agregado un 10 % de ruido gaussiano aleatorio. Esto produce un ruido de fondo de -40 dB en relación con el pico más alto.
Seleccione Archivo > Abrir base de datos del proyecto y abra la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Tutorials\Spectral Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025>Examples\Tutorials\Spectral Analysis.fpd. Abra la carpeta Tutorials y la subcarpeta Cross Spectral Analysis y haga doble clic en Data para abrir el diagrama 2D.
Este es un diagrama para ambas señales, cada una con 1024 valores en coma flotante.
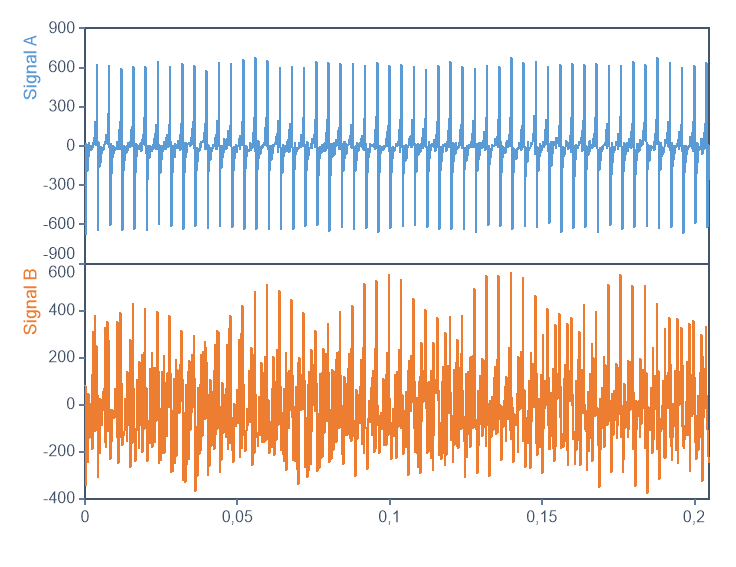
En el dominio del tiempo, solose puede observar que existen tanto similitudes como diferencias significativas.
Espectros de Fourier
Cierre el diagrama y seleccione el conjunto de datos Signal A, la señal de referencia.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis espectral y, a continuación, Análisis de Fourier. Allí se selecciona Espectro de Fourier. Tenga en cuenta que el resultado de algunos procedimientos espectrales depende del orden de los conjuntos de datos seleccionados. Por lo tanto, siempre debe comprobar cuidadosamente si la asignación que aparece en la lista con el título "3) Asignar conjuntos de datos" es correcta. Si el orden no es correcto, seleccione una entrada y muévala hacia arriba o hacia abajo pulsando los botones de flecha situados encima de la lista. En nuestro ejemplo, la señal A debería ser la primera entrada. A continuación, pulse el botón Siguiente.
Seleccione Amplitud como Tipo de espectro. Seleccione Cos3 Minimum Sidelobe -71 dB W=3 como Tipo de ventana. Asegúrese de que la Longitud de la FFT está establecida en la Longitud de datos o a 1024. Seleccione Número máximo de picos en Opciones e introduzca el valor 9. A continuación, establezca Límite crítico ruido blanco % en Ninguno. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
La representación gráfica del espectro de Fourier en el asistente para análisis debería tener este aspecto:
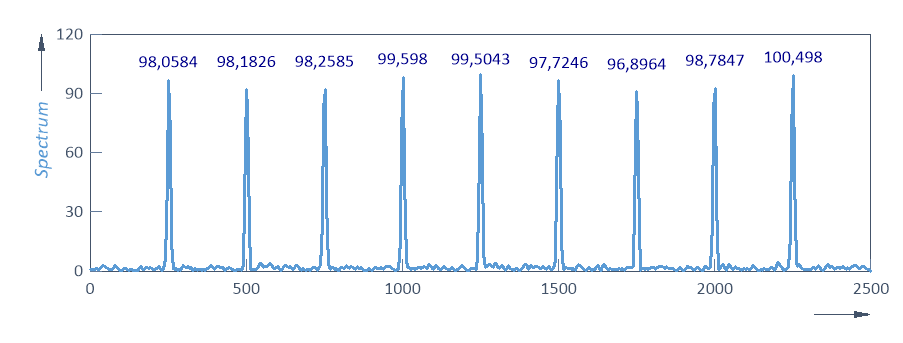
Normalmente, los picos no están centrados en los canales de Fourier, y el espaciado de los armónicos respecto al centro de los canales tampoco es constante. Cuando el espaciado es menor, las amplitudes son mayores. También se debe tener en cuenta que la funcion ventana hace que parte de la información espectral se distribuya a los canales vecinos. Por esta razón, las amplitudes mostradas de los picos son solo aproximadamente el 75 % de las amplitudes reales de los armónicos.
Haga clic en Cancelar y repita los mismos pasos para el conjunto de datos Signal B.
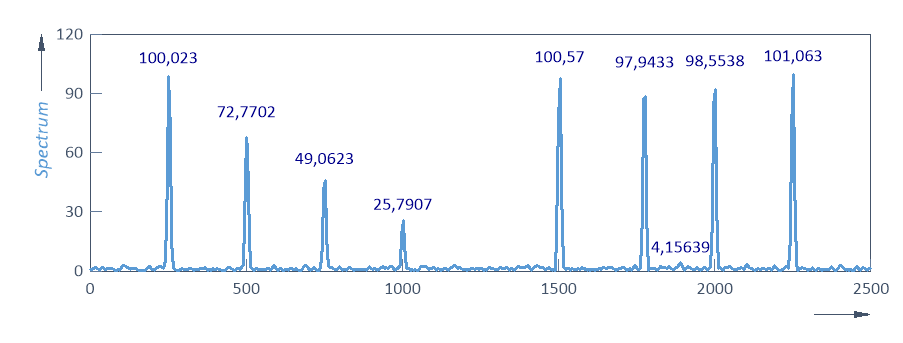
La única diferencia apreciable en el segundo espectro es la reducción de las amplitudes en comparación con los componentes espectrales originales. El cambio en la frecuencia de los componentes sexto y séptimo es más difícil de reconocer.
Espectros cruzados de Fourier
Haga clic en Cancelar para salir del asistente. Seleccione los dos conjuntos de datos Signal A y Signal B manteniendo pulsada la tecla Ctrl mientras realiza la selección.
Haga clic en Insertar[Análisis] > Asistente para análisis.
Seleccione la categoría Análisis espectrales y, a continuación, Procedimientos espectrales para dos señales. Allí se selecciona Espectro cruzado de Fourier. Haga clic en el botón Siguiente.
Al igual que en el análisis de Fourier, seleccione la opción Amplitud para el Tipo de espectro. Para Tipo de ventana, seleccione el valor Cos 3 Minimum Sidelobe -71 dB W=3. Asegúrese de que la Longitud de la FFT está establecida en la Longitud de datos o a 1024. Seleccione Número máximo de picos en Opciones e introduzca el valor 9. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
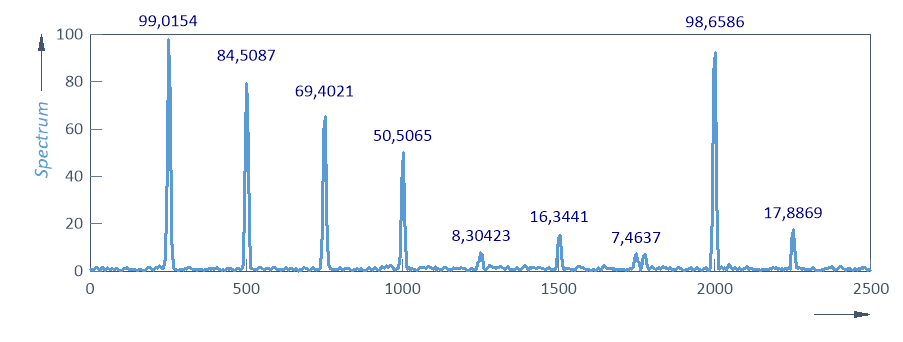
Si solo varían las amplitudes, como ocurre en los componentes segundo a cuarto, las amplitudes espectrales cruzadas se sitúan entre las de los dos espectros.
En la quinta posición, solo se produce un armónico en una de las dos señales. No obstante, aquí se produce un pequeño pico. Se trata del espectro cruzado entre el componente de señal de alta potencia de la señal de referencia y el ruido de la segunda señal en esta frecuencia. Tenga en cuenta que la existencia de un pico en una frecuencia determinada no significa que los armónicos estén presentes en ambas señales. En este ejemplo, solo hay un componente espectral a esta frecuencia en la primera de las dos señales.
En la sexta posición se pueden ver los efectos cuando dos picos se desvían entre sí solo un 0,1 % del rango de Nyquist. Sigue habiendo un componente de espectro cruzado, pero es pequeño. Solo hay un desplazamiento de 2,5 Hz en un espectro que abarca 2500 Hz.
En la séptima posición, la frecuencia se desvía un 1 % del rango de Nyquist, es decir, 25 Hz en este ejemplo. Ahora hay dos componentes de espectro cruzado, uno en la frecuencia central de la primera señal y otro en la frecuencia central de la segunda señal. Los picos están causados por el ruido, ya que aquí no hay contenido espectral cruzado relevante.
Si la fase se desvía en π, como en el caso del octavao componente, la diferencia es la misma que cuando se comparan señales seno y coseno. Se mantiene la amplitud total. En el caso del desplazamiento de fase π/2 más desfavorable, como ocurre en el noveno componente, se pierde gran parte de la amplitud espectral cruzada.
Periodograma cruzado
Se aplican los mismos principios al periodograma cruzado que al periodograma, que promedia los segmentos individuales solapadaos para producir una estimación de Fourier con varianza reducida, aunque con menor resolución espectral.
Seleccione el algoritmo Periodograma cruzado. Asegúrese de que Amplitud está seleccionada y que el Tipo de ventana está ajustado a Cos 3 Minimum Sidelobe -71 dB W=3. La Longitud del segmento es la Longitud de datos/4 o 256 y la Longitud de la FFT se establece en la Longitud del segmento o 256. El Solapamiento debe ser del 50 %. Seleccione Número máximo de picos en Opciones e introduzca el valor 9. Si no hay etiquetado visible sobre los picos, haga clic en Etiquetado hasta que aparezca el etiquetado de amplitud.
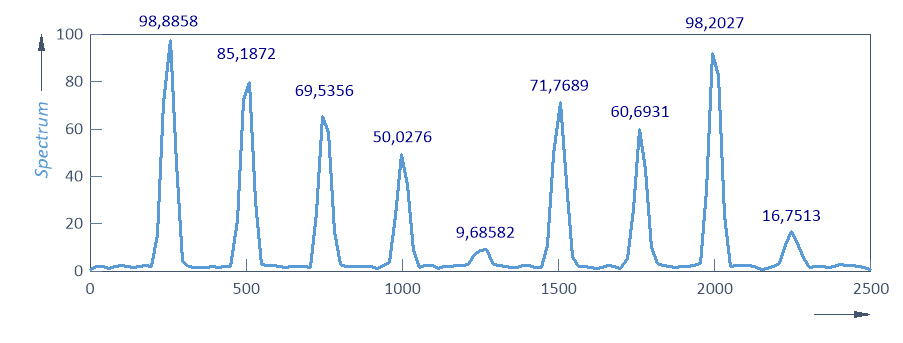
Los picos son más amplios porque la resolución espectral es solo una cuarta parte del espectro cruzado de un solo segmento. Esta resolución de frecuencia reducida es un factor significativo en este ejemplo.
La reducción de la varianza da lugar a un espectro mucho más alisado. Las amplitudes espectrales cruzadas de los valores de entrada se determinan con mayor precisión. El espectro cruzado entre el armónico y el ruido en la posición de quinta frecuencia es ahora un pico alisado de baja potencia.
La mayor diferencia es reconocible en los componentes sexto y séptimo. Debido a la reducción de la resolución de frecuencia, ahora hay un claro solapamiento entre los componentes. El resultado del desplazamiento de 2,5 Hz es una amplitud del espectro cruzado que se reduce en menos de un tercio. Incluso el desplazamiento de 25 Hz provoca una reducción de la amplitud del espectro cruzado de menos de la mitad de la amplitud que se habría generado con frecuencias completamente idénticas.
Los próximos pasos mejorarán la resolución del periodograma cruzado. Dado que no se está realizando un análisis espectral cruzado con un alto rango dinámico (es decir, no se buscan componentes espectrales de muy baja potencia), se utiliza una ventana de ponderación que no cause tanta pérdida de resolución en el dominio de la frecuencia. La resolución también se duplica utilizando un segmento de la mitad de la longitud del conjunto de datos. Para mejorar la varianza o, al menos, generar un espectro más alisado, se promedia un mayor número de segmentos aumentando el solapamiento.
Establezca el Tipo de ventana en Cos2 Hanning -31 dB W=2, la Longitud del segmento en 512, la Longitud de la FFT en la Longitud del segmento o 512. Cambie el Solapamiento al 90 %.
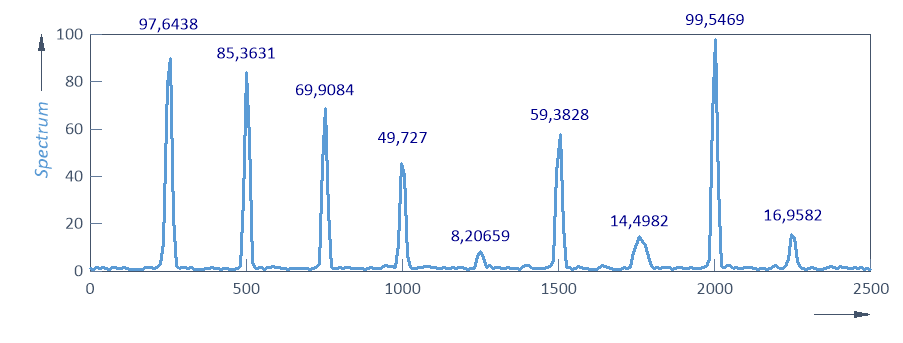
Tenga en cuenta que los picos son más nítidos y que la amplitud de los picos del espectro cruzado para los componentes sexto y séptimo, cuyos componentes originales difieren en frecuencia, se ha reducido. El espectro está ligeramente menos alisado, pero las amplitudes son ahora algo mayores debido a la reducción del desbordamiento hacia las líneas espectrales vecinas.
Coherencia
Si se utilizan varios segmentos, se puede generar un espectro de coherencia. La coherencia es 1 si los componentes son similares a una frecuencia determinada y 0 si las señales son diferentes o no están correlacionadas en absoluto. Se trata de un método habitual para buscar rangos de un espectro en los que una señal de salida es incoherente, es decir, los componentes espectrales no guardan relación con la señal de entrada.
Seleccione el procedimiento Coherencia y el tipo de espectro Coherencia. Deje todas las configuraciones del ejemplo del periodograma cruzado como están. Haga clic en el botón Etiquetado para desactivar el etiquetado de los picos.
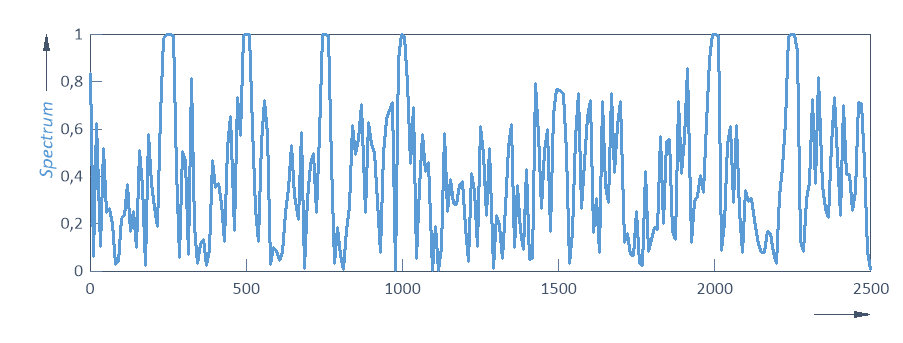
Aunque los valores de entrada de las dos señales difieren en amplitud, esto no influye en la MSC (Magnitude-Squared Coherence). Los cuatro primeros componentes mostrados tienen una coherencia que alcanza 1.
El quinto componente, que solo está presente en una señal, no muestra nada por encima de la línea de base.
Los componentes de la sexta posición, que se caracterizan por una diferencia de frecuencia de solo 2,5 Hz entre las dos señales, tienen una coherencia mayor que los componentes de la séptima posición, con una diferencia de frecuencia de 25 Hz. Tenga en cuenta que este séptimo componente produce una coherencia uniformemente baja.
El MSC también es independiente de la fase. Los componentes de las posiciones octava y novena generan coherencia 1 a pesar del desplazamiento de fase.
Espectro de la relación señal-ruido
Si se utilizan varios segmentos, también es posible generar un espectro de relación señal-ruido. Este utiliza los valores de coherencia para estimar la relación señal-ruido de cada frecuencia del espectro.
Seleccione la relación señal-ruido dB como tipo de espectro.
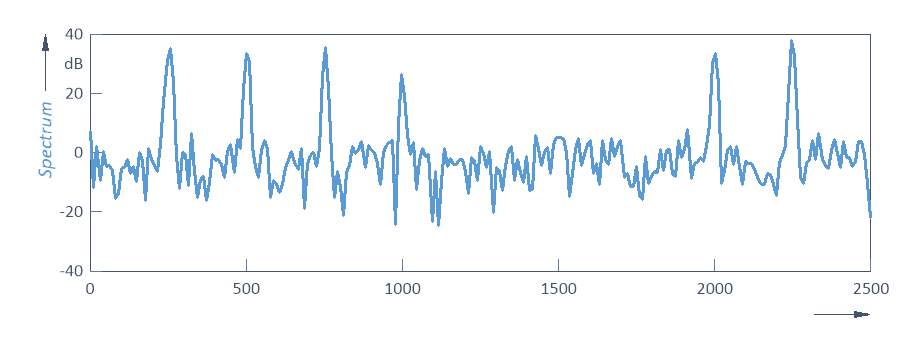
Recuerde que el ruido de fondo es de aproximadamente -40 dB para ambas señales. Aquí puede ver picos que se elevan unos 40 dB por encima del ruido de fondo. Al igual que en el caso de la coherencia, los componentes con amplitud cambiante y fase cambiante muestran una relación señal-ruido completa o casi completa. La desviación de 2,5 Hz en la frecuencia de los componentes se traduce en un ligero aumento de la relación señal-ruido. En cambio, los componentes que se desvían 25 Hz ya no se distinguen del ruido.
Función de transferencia
La función de transferencia de Fourier representa las propuedades de transferencia de un sistema en el dominio de frecuencias. En este ejemplo, la segunda señal siempre contiene la misma o menor potencia en todas las frecuencias, excepto en los dos casos en los que hay desplazamientos de frecuencia.
A diferencia de los espectros de coherencia y de relación señal-ruido, una función de transferencia puede calcularse a partir de un único segmento. Por lo tanto, se utilizan la misma configuración que en el ejemplo del espectro cruzado.
Seleccione la Función de transferencia y el Tipo de espectro dB. Seleccione Cos 3 Minimum Sidelobe -71 dB W=3 como Tipo de ventana. Establezca la Longitud de la FFT en la Longitud de datos o en1024. Desactive el etiquetado de los picos. Haga clic en el diagrama superior y, a continuación, en el símbolo Activar cursores (el primero de la barra de herramientas situada debajo de los diagramas).
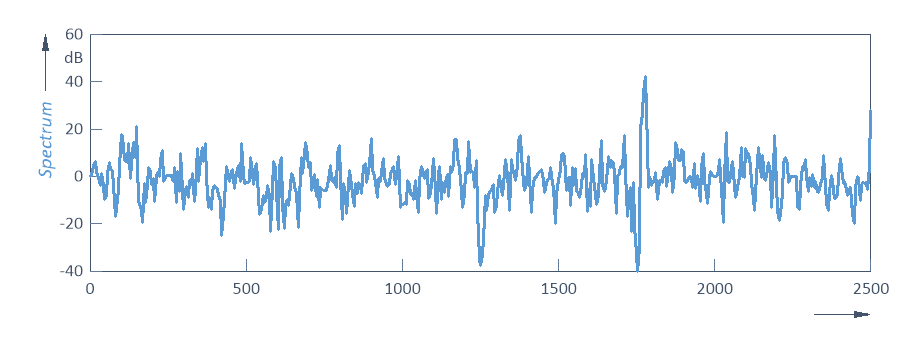
Coloque el cursor en 250 Hz, la posición del primer componente. El valor es de aproximadamente 0,17 a 0,18 dB. Colocando el cursor en 500, 750 y 1000 se obtendrán los valores -2,5 dB, -6,0 dB y -11,7 dB.
Estos valores corresponden a la reducción de la amplitud de la segunda señal en 1/4, 1/2 y 3/4.
Tenga en cuenta que hay un mínimo en la función de transferencia de 1250 Hz, donde el pico de la segunda señal ha desaparecido por completo.
También hay un mínimo en la función de transferencia en 1750 Hz, donde de nuevo no hay ningún pico en la señal de salida, y un pico pronunciado en la función de transferencia de 1775 Hz, donde hay un pico pronunciado en la señal de salida pero ninguno en la señal de entrada.
Aplicar una función de transferencia a los datos de entrada
Tenga en cuenta que, en aplicaciones prácticas, carece de sentido calcular una función de transferencia utilizando señales como las usadas en las secciones anteriores. Se puede observar que la señal B no puede ser una respuesta de un sistema LTI (Linear Time-Invariant System), ya que se ha producido un desplazamiento de frecuencia mientras que los sistemas LTI solo varían las fases y amplitudes de los componentes espectrales existentes. Además, la señal de entrada debe excitar todas las "frecuencias en" el sistema LTI para obtener una imagen completa del sistema LTI y, por tanto, una función de transferencia bien definida. Una señal de entrada de este tipo sería, por ejemplo, ruido blanco.
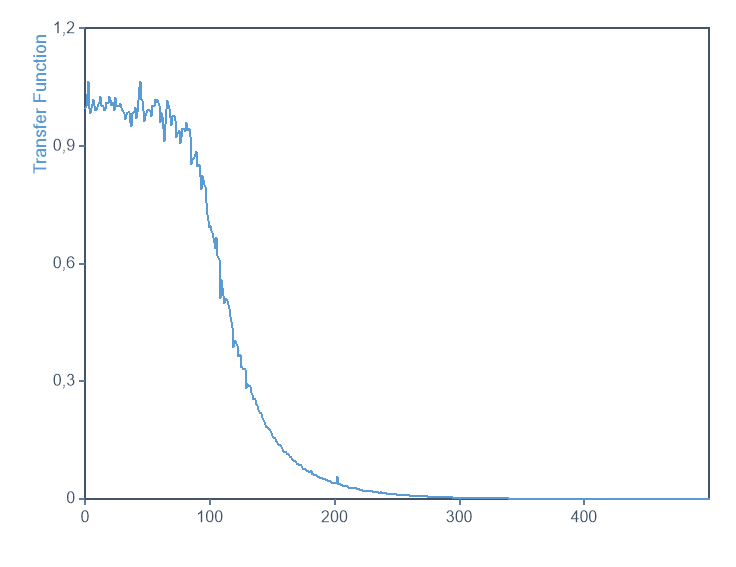
Para demostrarlo, la base de datos del proyecto con ejemplos contiene otro conjunto de datos Input Noise y un objeto llamado Output Noise, que es una versión de filtro de paso bajo del ruido de entrada. Ya se ha creado el objeto Transfer Function para calcular la función de transferencia del filtro paso bajo utilizando estas señales. Un diagrama con el mismo nombre lo visualiza. El filtro paso bajo es un filtro Butterworth de orden 4 con una frecuencia de corte de 100 Hz.
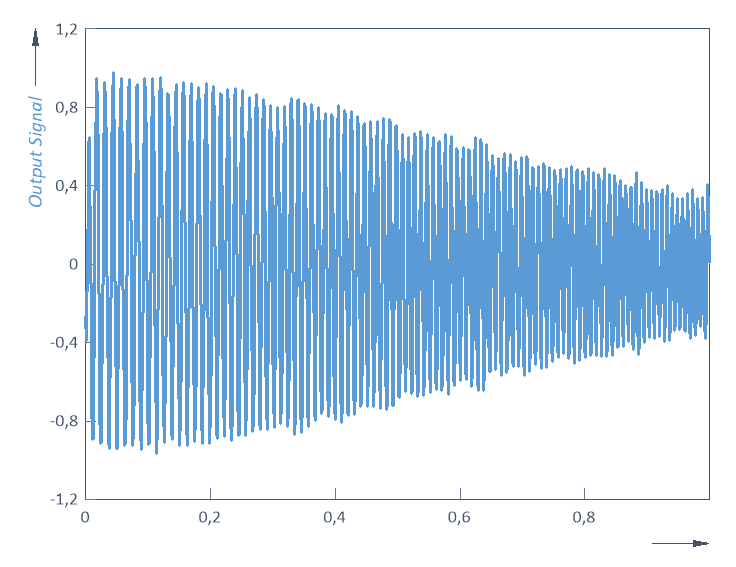
Como ejercicio final, la función de transferencia se aplicará a una señal de entrada para estimar la señal de salida. Seleccione el objeto Input Signal, que muestra un seno de frecuencia variable cuya frecuencia aumenta linealmente de 75 Hz a 125 Hz. Haga clic con el botón derecho del ratón, seleccione Insertar nuevo objeto y, a continuación, haga clic en Fórmula. Introduzca la siguiente fórmula: IRFFTn(FFTn('Input Signal') * 'Transfer Function'). Ahora haga clic en Ejecutar para probar la fórmula. Debería recibir una señal con 1000 puntos. Cierre la ventana de la fórmula. Seleccione de nuevo el nombre de la fórmula y pulse la tecla F2. Introduzca ahora el nuevo nombre Output Signal. DLa fórmula calcula el espectro de la señal de entrada y lo multiplica por la función de transferencia. Este sencillo cálculo es posible porque una convolución en el dominio del tiempo corresponde a una simple multiplicación en el dominio de la frecuencia. Si multiplica los espectros, debe asegurarse de que el número de frecuencias y los incrementos de frecuencia de ambos espectros sean idénticos. Para simplificar al máximo este tutorial, la función de transferencia se ha calculado a partir de un único segmento cuya longitud corresponde al ruido de entrada y también a la señal de seno de frecuencia variable. Si se hubieran promediado los segmentos solapados, la función de transferencia habría sido más alisada y más corta.
Se ha calculado un conjunto de datos con 1000 valores reales cuya amplitud disminuye al aumentar la frecuencia. La frecuencia de corte de 100 Hz se alcanza exactamente en el centro de la señal de seno de frecuencia variable. Allí, la amplitud de la señal de salida se atenúa en -3 dB, como era de esperar.
Bibliografía
•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.