Puede utilizar este objeto de análisis para determinar la matriz de Rainflow o la matriz (de transición) de Markov de una señal. A continuación, puede extraer de las matrices diversos colectivos de un parámetro, por ejemplo, las frecuencias de los valores picos, utilizando el objeto de análisis Recuento de Rainflow.
Matriz
La matriz de Markov contiene las frecuencias absolutas de todas las transiciones de la función de tiempo de carga. Primero se determinan todos los puntos de inversión de la función de tiempo de carga. Estos puntos de inversión se clasifican según la división de clases. Un par de puntos de inversión consecutivos se considera una transición. La clase del punto "de" selecciona la fila de la matriz y la del punto "a", la columna correspondiente. La transición se contabiliza en la posición de la matriz resultante.
Las frecuencias de los valores picos, los rangos y los cruces de límite de clase pueden extraerse de la matriz de Markov. La matriz de Markov no tiene suficientemente en cuenta los requisitos del análisis de vida a fatiga, ya que los ciclos de carga más grandes, en los que se producen cambios de carga más pequeños, se descomponen en una secuencia de pequeñas transiciones.
El algoritmo Rainflow evita este inconveniente. Aquí no se contabilizan las transiciones entre puntos de inversión sucesivos, sino las histéresis cerradas (pares de rango). Se trata de cambios de carga que como mínimo vuelven a alcanzar su punto de partida. En el caso de un ciclo de carga grande que contenga cambios de carga más pequeños, estos se contabilizan primero como histéresis pequeñas y el ciclo de carga grande se contabiliza al final como histéresis grande. Las histéresis también se denominan pares de rango. La siguiente ilustración muestra cómo se elimina un par de rango de la curva sin perder el ciclo de carga grande:
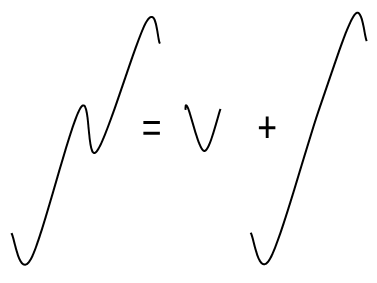
La ilustración anterior también muestra que un par de rango de este tipo está formado por una transición ascendente y otra descendente del mismo tamaño. En la forma "de"-"a" de la matriz de Rainflow, un par de rango de este tipo se contabiliza dos veces, una como ascenso y otra como descenso. De forma alternativa, también se puede crear la forma asimétrica de la matriz. En este caso, solo se contabiliza la primera transición del par de rango, que puede ser ascendente o descendente. Por tanto, esta forma de matriz distingue entre pares de rango "positivos" y "negativos". La suma de recuento de la matriz asimétrica es solo la mitad de grande que la de la matriz simétrica. Se puede obtener la matriz simétrica a partir de la matriz asimétrica sumando la matriz asimétrica con su transpuesta.
El resultado del recuento es una serie de señales con componente Z. Su componente Y contiene la matriz con los valores de recuento, el componente X contiene las medias de las clases "de" y el componente Z contiene las de las clases "a". También se puede emitir la matriz de Rainflow en la presentación rango-media. En este caso, el componente X contiene los límites inferiores de las clases de rangos. Todas las histéresis con la misma distancia absoluta entre "de" y "a" entran en una clase de rangos. El componente Z contiene las medias de las clases de valores medios. Todas las histéresis con el mismo valor medio de "de" y "a" entran en una clase de valores medios. También en este caso, las histéresis cerradas solo se contabilizan una vez.
Residuo
El inconveniente del método Rainflow es que no todos los puntos de inversión cumplen el algoritmo Rainflow. A menudo queda un residuo. El residuo suele ser una curva en zigzag con amplitudes ascendentes y descendentes. Puede excluir el residuo de la matriz, incluir solo una histéresis cerrada "a-b-a" en el centro del residuo en la matriz o incluir el residuo completamente en la matriz. En particular, si se van a extraer colectivos de un solo parámetro, como los valores picos, de la matriz de Rainflow, el residuo deberá incluirse en la matriz. Existen varios procedimientos para ello. El procedimiento implementado, descrito en [1], es especialmente equilibrado. El residuo se divide en el punto más alto y las dos mitades se unen entre sí en orden inverso. Esta secuencia cumple el algoritmo y se incluye en la matriz. De forma alternativa, puede incluir los semiciclos del residuo en la matriz con el valor de recuento 0,5 en cada caso, es decir, se asume la mitad de la cantidad de daño de una histéresis completa para cada semiciclo del residuo [2].
División de clases
El recuento se basa en la división del rango de valores de la función de tiempo de carga (conjunto de datos de origen) en clases discretas. Existen varios procedimientos para realizar esta división. Esencialmente, la posición de los límites de clase se especifica para todos los procedimientos. Los procedimientos solo difieren en la selección de los parámetros que debe introducir para especificar los límites de la clase. Las clases se forman como intervalos abiertos a por la derecha partir de los límites especificados, es decir, se asigna a cada clase el límite inferior. Una excepción es la clase superior, a la que también se asigna el límite superior. ¡Todos los valores por encima de la clase más alta o por debajo de la más baja no se tienen en cuenta!
La elección de una división de clases adecuada debe planificarse cuidadosamente, ya que solo los resultados determinados con la misma división de clases son directamente comparables. Los cambios de carga en la función del tiempo de carga que son menores que el ancho de clase solo se contabilizan si se encuentran en un límite de clase. Por tanto, la posición de los límites de clase influye en el resultado del recuento.
Histéresis
Con el fin de minimizar este efecto, se puede utilizar una histéresis (filtro de rango) para suprimir los rangos o los pares de rango pequeños. La histéresis es una variable independiente de la posición de los límites de clase. Solo se contabilizan los rangos o pares de rango cuya amplitud se corresponda como mínimo con la histéresis. La histéresis se especifica como porcentaje del ancho de clase o, en el caso de divisiones de clases no equidistantes, del ancho de clase medio.
Bibliografía
[1] de Jonge, J.B. (1980). Counting Methods for the Analysis of Load Time Histories. NLR Memorandum SB-80-106 U
[2] ASTM E1049-85(2017). Standard Practices for Cycle Counting in Fatigue Analysis. STM International, West Conshohocken, PA, 2017
Funciones FPScript utilizadas
Véase también
Residuo del algoritmo Rainflow