Con este objeto de análisis puede determinar las cantidades instantáneas amplitud instantánea, fase instantánea y frecuencia instantánea de las señales. La amplitud instantánea proporciona la curva de amplitud, la fase instantánea, la curva de fase, y la frecuencia instantánea, la curva de frecuencia de la señal que se va a analizar. Si la señal subyacente no tiene tendencia, la amplitud instantánea también coincide con la envolvente superior de la señal.
El cálculo de las cantidades instantáneas solo es adecuado para señales de un solo componente.
En el siguiente ejemplo, la amplitud instantánea y la frecuencia instantánea de un coseno de frecuencia variable modulado en amplitud se determina utilizando el objeto de análisis Magnitud instantánea:
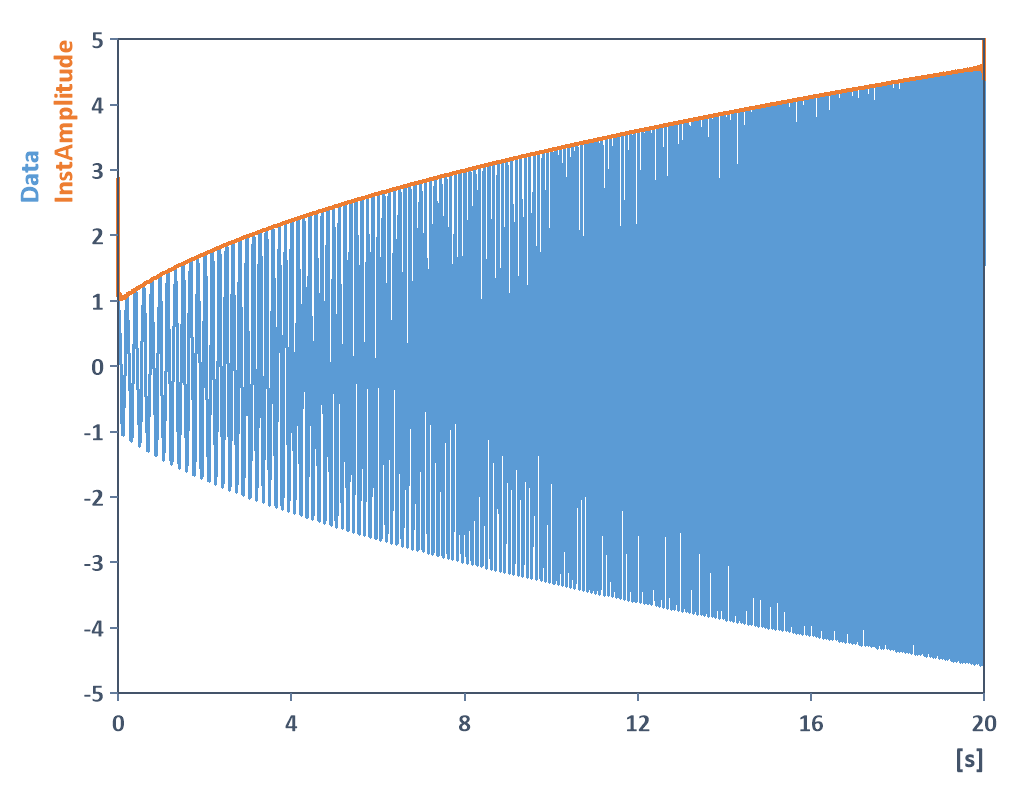
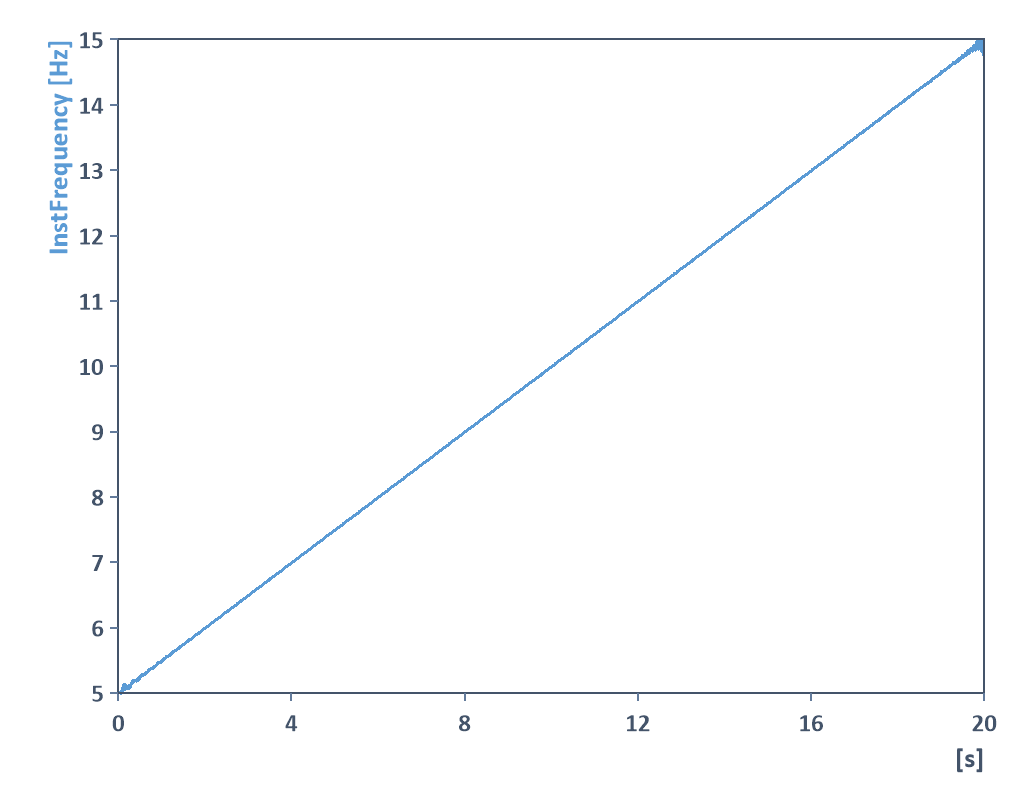
Por tanto, las cantidades instantáneas también pueden utilizarse para demodular señales (demodulación de amplitud, demodulación de fase, demodulación de frecuencia). Puede encontrar información al respecto en la ayuda en línea de la función AnalyticSinal.
Algoritmo
En la bibliografía inglesa, estas cantidades instantáneas suelen denominarse Instantaneous Amplitude (o Instantaneous Envelope), Instantaneous Phase o Instantaneous Frequency, y se calculan mediante la transformada de Hilbert. Encontrará más detalles en la ayuda en línea de la función de Hilbert o de la función AnalyticSignal.
Parámetro: Longitud de la FFT
La transformada de Hilbert realiza una transformada interna de Fourier (FFT) del conjunto de datos. La resolución de la FFT necesaria para el algoritmo se aumenta mediante el relleno de ceros (Zero-Padding), es decir, seleccionando una longitud de la FFT mayor que la longitud de los datos. Esto puede mejorar el resultado del cálculo. En el objeto de análisis se puede seleccionar la siguiente configuración para la longitud de la FFT:
Selección |
Significado |
|---|---|
Longitud de datos |
Ajusta la longitud de la FFT a la longitud de datos. |
Siguiente potencia de 2 |
Ajusta la longitud de la FFT a la siguiente potencia superior de 2. |
Parámetro: Eliminar tendencia
Para las señales que tienen una tendencia o un offset, primero hay que eliminar la tendencia para determinar las cantidades instantáneas. Las siguientes opciones de selección están disponibles en el objeto de análisis. Las opciones de selección corresponden a las opciones de selección de la eliminación de tendencias del objeto de análisis "Análisis de señales":
Selección |
Significado |
|---|---|
Constante |
Resta el valor medio del conjunto de datos. |
Lineal |
Resta la recta de mejor ajuste, es decir, la línea recta para la que la suma de los cuadrados de las desviaciones del conjunto de datos es mínima. |
Adaptativa |
Resta el valor medio de la curva envolvente superior e inferior. Este ajuste puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. |
Media móvil |
Resta la media móvil. Se puede introducir el ancho de intervalo necesario para calcular la media móvil. Este ajuste puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. El filtro de media móvil es un filtro de paso bajo. |
Filtro de desplazamiento de CC |
Filtro de paso alto para eliminar el desplazamiento de CC (filtro de paso alto IIR Butterworth). Se puede ajustar la frecuencia de corte y el orden (es decir, la pendiente) del filtro de paso alto. El filtro puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. |
Para determinar la tendencia constante o lineal, primero se calcula la media de la señal y, a continuación, se buscan el primer y el último cruce de nivel mediante este valor. Si se encuentran dos pasos a nivel, el valor medio o la recta de mejor ajuste solo se calcula para el rango entre estos dos pasos a nivel. Así se evitan los errores provocados por el ángulo de fase de las señales periódicas en los extremos del conjunto de datos. Si no se encuentra ningún cruce de nivel, se incluyen todos los valores en el cálculo. Los ajustes adecuados para eliminar una tendencia dependiente del tiempo suelen ser la sustracción de la media móvil y el filtro de desplazamiento de CC.
Ejemplo y detalles
Encontrará más información y detalles sobre el ejemplo anterior en la ayuda en línea de la función AnalyticSignal.