El objeto de análisis Análisis de órdenes síncronas de revolución calcula un análisis de órdenes para vibraciones dependientes de la velocidad de rotación. Las vibraciones medidas en máquinas rotativas muestran un espectro en el que los máximos se producen a frecuencias que corresponden a un múltiplo de la velocidad de rotación de la máquina. La aparición de estos máximos se debe a dos motivos diferentes. Por un lado, la máquina se puede considerar un sistema de transmisión no lineal, que se activa con una vibración armónica correspondiente a la velocidad de rotación. La no linealidad genera armónicos de esta vibración fundamental, que dan lugar a los máximos correspondientes. Por otra parte, una máquina de este tipo puede contener componentes cuya velocidad de rotación no sea igual a la velocidad de rotación fundamental, sino que corresponda siempre a un múltiplo fijo de esta velocidad. Por ejemplo, los distintos ejes de una caja de engranajes tienen velocidades de rotación diferentes. Sin embargo, los dientes de un engranaje o las bolas de un rodamiento también generan vibraciones que guardan una relación fija con la velocidad de rotación. Si se conoce esta relación, denominada orden, entre la frecuencia fundamental de un componente y la frecuencia fundamental de la máquina, se pueden asignar específicamente los máximos determinados del espectro a uno o varios componentes de la máquina. Esto puede servir, por ejemplo, para aislar la causa de las resonancias.
En el procedimiento utilizado aquí, primero se lleva a cabo una conversión de la frecuencia de muestreo de la señal de tiempo (remuestreo síncrono de revolución), de modo que la señal ya no está disponible en pasos de tiempo equidistantes, sino en pasos de ángulo de rotación equidistantes (es decir, intervalos de revolución equidistantes). Esto permite realizar un análisis de órdenes de forma eficaz, ya que el espectro de frecuencias (es decir, la transformada de Fourier) de la señal convertida al dominio de rotación proporciona inmediatamente el denominado espectro de órdenes (para más detalles, véase RevolutionSyncSampling):
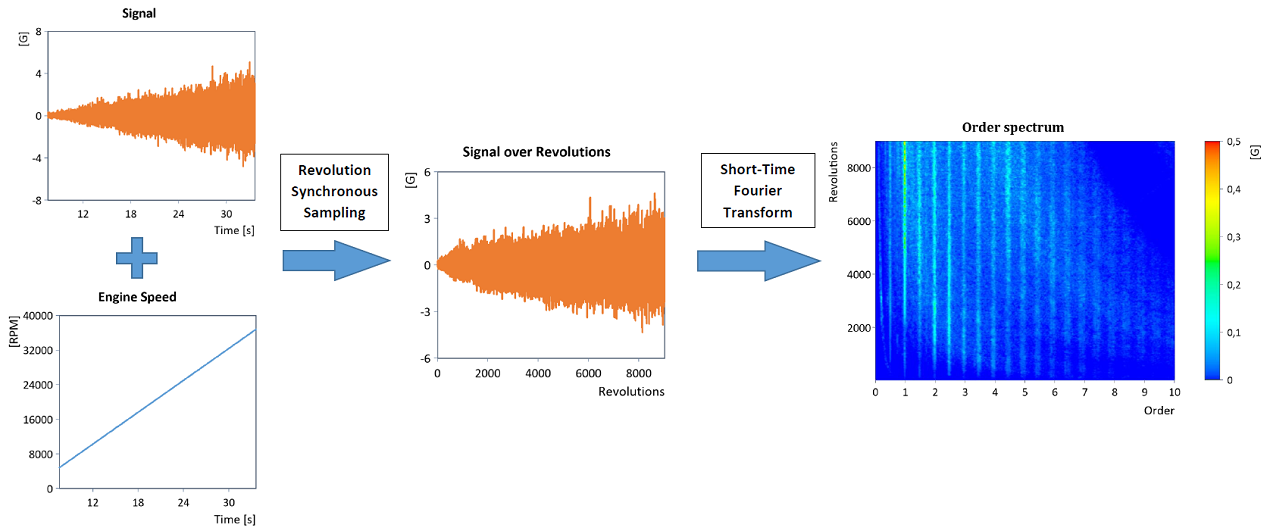
El recorrido de órdenes se obtienen a partir del espectro de órdenes extrayendo las líneas de orden individuales (cortes de orden).
Para el análisis de órdenes se utilizan dos métodos de medición principales. Durante una rampa de arranque, la vibración y la velocidad de rotación instantánea se miden de forma sincronizada mientras la máquina suele rodar lentamente desde su velocidad de rotación mínima hasta su velocidad máxima (análisis de rampa de arranque). En el segundo procedimiento, primero se lleva la máquina a una velocidad de rotación determinada y luego se mide la vibración para esta velocidad (análisis de órdenes con velocidad de rotación constante). El objeto de análisis Análisis de órdenes síncronas de revolución soporta ambas variantes. Además, el análisis de órdenes mediante remuestreo sincronizado con la revolución es extremadamente flexible y puede realizarse incluso para conjuntos de datos de velocidad de rotación ruidosos y no monótonos (análisis de órdenes con velocidad de rotación variable).
Pestaña Datos
Esta pestaña especifica los datos de entrada y los parámetros para la transformación del dominio de tiempo al dominio de rotación (para más detalles, véase también RevolutionSyncSampling).
Señales en el dominio del tiempo
La señal de tiempo que se va a analizar para el objeto de análisis debe estar disponible en la estructura de datos señal. La velocidad de rotación puede especificarse en la estructura de datos señal (corresponde a un análisis de rampa de arranque o a un análisis de órdenes con velocidad de rotación variable) o como valor escalar (corresponde a un análisis de órdenes con velocidad de rotación constante o a una frecuencia fundamental fija).
Si faltan unidades o la “gestión de unidades” está desactivada, la velocidad de rotación siempre se interpreta en la unidad [1/min] y el componente X de la señal de tiempo en la unidad [s].
La velocidad de rotación instantánea suele medirse mediante un generador de impulsos que registra un determinado número de impulsos por revolución. Puede convertir la señal de impulsos resultante directamente en una señal de velocidad de rotación. Para ello, seleccione la opción La velocidad de rotación es una señal de impulso e introduzca el Número de impulsos por revolución. La señal de impulso se convierte en una señal de velocidad de rotación mediante la función ImpulseToFrequency.
Remuestreo en el dominio de rotación
Para el remuestreo del dominio del tiempo al dominio de rotación, se dispone de tres modos diferentes. En la mayoría de las aplicaciones prácticas, el remuestreo lineal es suficiente:
Método de remuestreo |
Descripción |
|---|---|
Interpolación lineal |
La señal de tiempo se analiza mediante interpolación lineal en los puntos de tiempo (no equidistantes) de los nodos de rotación equidistantes antes de transferirla al dominio de rotación. La transformación es, por tanto, rápida, pero puede causar efectos Aliasing en el cáculo posterior del espectro de órdenes. |
Interpolación de spline |
La señal de tiempo se analiza mediante interpolación de spline en los puntos de tiempo (no equidistantes) correspondientes a los puntos de referencia de revolución equidistantes antes de transferirla al dominio de rotación. En comparación con el remuestreo lineal, la interpolación de spline es ligeramente más lenta, pero se reducen los efectos Aliasing. |
Remuestreo FFT |
La señal de tiempo se analiza mediante remuestreo FFT en los puntos de tiempo (no equidistantes) correspondientes a los puntos de referencia de revolución equidistantes antes de transferirla al dominio de rotación. La señal de tiempo se transforma primero al dominio de la frecuencia, donde se añaden ceros, y luego se transforma de nuevo al dominio del tiempo. El remuestreo mediante la transformada de Fourier conduce a un resultado casi ideal, ya que no se añaden componentes de señal de alta frecuencia. Esto elimina prácticamente los efectos Aliasing al calcular el espectro de órdenes, pero el tiempo de cálculo aumenta considerablemente. |
Si se selecciona el método de remuestreo de FFT o de splines se debe especificar un Factor de remuestreo mediante el cual se incrementa la frecuencia de muestreo de la señal durante el algoritmo de transformación.
Independientemente del método de remuestreo seleccionado, se debe especificar el número de Puntos de datos por revolución para que la señal se transforme al dominio de rotación. Determina el muestreo de la señal transformada al dominio de rotación. La mitad de este valor determina la orden máxima que puede calcularse mediante el análisis de Fourier en el espectro de órdenes, según el teorema de muestreo de Nyquist
Existen dos modos para determinar el número de puntos de datos por revolución:
Puntos de datos por revolución |
Descripción |
|---|---|
Automático (ajuste a orden máxima) |
Calcula un valor automático para el número de puntos de datos por revolución, de forma que el orden teóricamente mayor que se produce en la señal pueda seguir calculándose mediante el análisis de Fourier. El valor calculado automáticamente puede limitarse mediante un valor Límite libremente ajustable. |
Valor fijo |
Se puede introducir cualquier valor fijo para el número de puntos de datos por revolución. |
Corrección de tendencia (dominio de rotación)
En muchos ejemplos de aplicación, un desplazamiento de CC demasiado grande da lugar a una representación visualmente inadecuada en el gráfico de contorno del espectro de órdenes, en el que domina el componente de CC. Por lo tanto, es ventajoso filtrar dicho componente de CC. Para ello, para la señal transformada al dominio de rotación se puede ajustar el correspondiente filtro de paso alto de desplazamiento de CC con Frecuencia de corte (orden) y Orden del filtro (pendiente de filtro) ajustables (para más detalles sobre el filtro de paso alto de desplazamiento de CC, véase la funciónDCRemovalFilter).
Pestaña Opciones
Esta pestaña especifica el espectro de órdenes calculado o las cortes de orden (extracción de las líneas de orden a partir del espectro de órdenes). El espectro de órdenes se determina mediante el análisis clásico de frecuencias utilizando la función STFTSpectrumde la señal transformada al dominio de rotación (es decir, se realiza un análisis de Fourier para los segmentos de datos superpuestos). Los cortes de orden se calculan mediante la función OrderCuts, es decir, las líneas de orden se recortan del espectro de órdenes.
Salida
Están disponibles los siguientes cuatro modos de salida del análisis de órdenes (sincronizado con la revolución):
Modo |
Descripción |
|---|---|
Espectro de órdenes |
Calcula el espectro de órdenes (mediante el análisis de Fourier) de la señal transformada al dominio de rotación. |
Extraer órdenes del espectro de órdenes (como lista) |
Las curvas de órdenes individuales se extraen del espectro de órdenes (cortes de orden). Los cortes de orden se devuelven en la estructura de datos Lista. |
Extraer órdenes del espectro de órdenes (como series de señales) |
Las curvas de órdenes individuales se extraen del espectro de órdenes (cortes de orden). Los cortes de orden se devuelven en la estructura de datos serie de señales. |
Análisis de órdenes RMS promediado |
Calcula el nivel RMS total de cada orden. Este modo es adecuado para el análisis de órdenes a velocidades de rotación constantes. El resultado devuelto es una señal (X = orden, Y = valor RMS). |
Tipo de espectro y resolución
El espectro de órdenes puede calcularse y obtenerse en distintos formatos. Los tipos de espectro corresponden a los tipos de espectro del objeto de análisis Análisis espectral tiempo-frecuencia (véase también la función STFTSpectrum).
En la representación de amplitud se pueden ver las amplitudes, mientras que en la pantalla RMS, las contribuciones RMS de los órdenes individuales. En la representación normalizada en dB, el pico más alto está a 0 dB, un pico a -3 dB tendría la mitad de potencia y un pico a -6 dB tendría la mitad de amplitud. El campo Rango máximo de dB solo está activado y se muestra para los formatos dB y dB, normalizado. La limitación de dB afecta a los valores finales del escalado automático y, por tanto, también al degradado de color en el espectrograma. Introduzca 0 en este campo para obtener un rango ilimitado. Normalmente se selecciona RMS como tipo de espectro para el análisis de órdenes (configuración Default).
La calidad del espectro de órdenes depende fundamentalmente de la elección del tamaño de cada segmento de datos, longitud del segmento, y de la magnitud de solapamiento, Solapamiento en %. La longitud del segmento está claramente definida por la Resolución del orden ajustable (por ejemplo, una resolución de orden de 1/32 da como resultado una longitud de segmento de 32 * número de puntos de datos por revolución). La longitud del segmento y la resolución del orden son, por tanto, antiproporcionales. En general, se recomienda un alto nivel de redundancia. La longitud del segmento debe ser tan pequeña como sea posible para conseguir una alta resolución de revolución/tiempo/velocidad de rotación, y tan grande como sea necesario para conseguir una alta resolución del orden. Este compromiso está siempre presente cuando se trabaja con la STFT. Para aumentar la redundancia y mejorar la calidad del espectro de órdenes, se puede establecer un porcentaje de solapamiento de los segmentos de datos. Esto aumenta la resolución de revolución/tiempo/velocidad de rotación, mientras que la resolución del orden sigue siendo la misma.
Los datos no se tienen en cuenta para la configurción de espacio en número de revoluciones. Este ajuste solo debe seleccionarse para series temporales muy largas con contenido espectral que cambia lentamente.
Comentarios sobre los requisitos de memoria: Para la STFT, se calculan y guardan FFT independientes para cada segmento de datos. Para minimizar los requisitos de memoria, debe evitar valores de solapamiento altos, ya que esto aumenta drásticamente el número de segmentos. El número de segmentos no depende linealmente del solapamiento y aumenta bruscamente a partir de valores de aproximadamente el 70 %. Aunque FlexPro permite solapamientos de hasta el 95%, los valores superiores al 50 - 70 % suelen generar pocas ganancias.
Ventana
FlexPro ofrece una variedad de ventanas de ponderación para reducir el manchado espectral. La alta redundancia que puede lograrse solapando las ventanas compensa la pérdida de información causada por la supresión de datos en los bordes de cada ventana. La ventana de ponderación conduce a una definición más nítida de las líneas espectrales en el resultado. Sin embargo, las amplitudes del espectro y la potencia también se reducen.
En la lista de selección Normalización, dispone por tanto de dos opciones de normalización en función de la ventana de ponderación. Si se selecciona Amplitud, se normaliza la ganancia de la ventana de ponderación utilizada, es decir, la suma de todos los valores de la ventana de ponderación dividida por su número. Esto compensa la atenuación de las amplitudes causada por la ventana de ponderación de los datos y es especialmente adecuado para medir picos en el espectro de órdenes. Si selecciona Potencia, se compensa la pérdida de potencia, es decir, se utiliza como factor de normalización la relación de la suma de los cuadrados de los datos antes y después de la ventana de ponderación. De este modo, la energía total del espectro de órdenes corresponde siempre a los datos anteriores a la ventana de ponderación.
El campo de Ajuste de ancho se utiliza para definir el ancho espectral y, por tanto, el rango dinámico, de las ventanas ajustables. Este campo está desactivado para las ventanas de ancho fijo.
Resultado del espectro de órdenes
Al seleccionar el modo de salida del espectro de órdenes, pueden seleccionarse los siguientes tipos de resultados.
Resultado |
Descripción |
|---|---|
Y = amplitud, X = orden, Z = revolución |
Serie de señales en la que cada señal contiene las amplitudes para un valor de revolución específico en función del orden. |
Y = amplitud, Z = orden, X = revolución |
Serie de señales en la que cada señal contiene las amplitudes de un determinado orden en función de las revoluciones. |
Y = amplitud, X = orden, Z = tiempo |
Serie de señales en la que cada señal contiene las amplitudes en un instante determinado en función del orden. |
Y = amplitud, Z = orden, X = tiempo |
Serie de señales en la que cada señal contiene las amplitudes de un determinado orden en función del tiempo. |
Y = amplitud, X = orden, Z = velocidad de rotación |
Serie de señales en la que cada señal contiene las amplitudes a una velocidad de rotación específica en función del orden. Se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
Y = amplitud, Z = orden, X = velocidad de rotación |
Serie de señales en la que cada señal contiene las amplitudes de un determinado orden en función de la velocidad de rotación. Se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
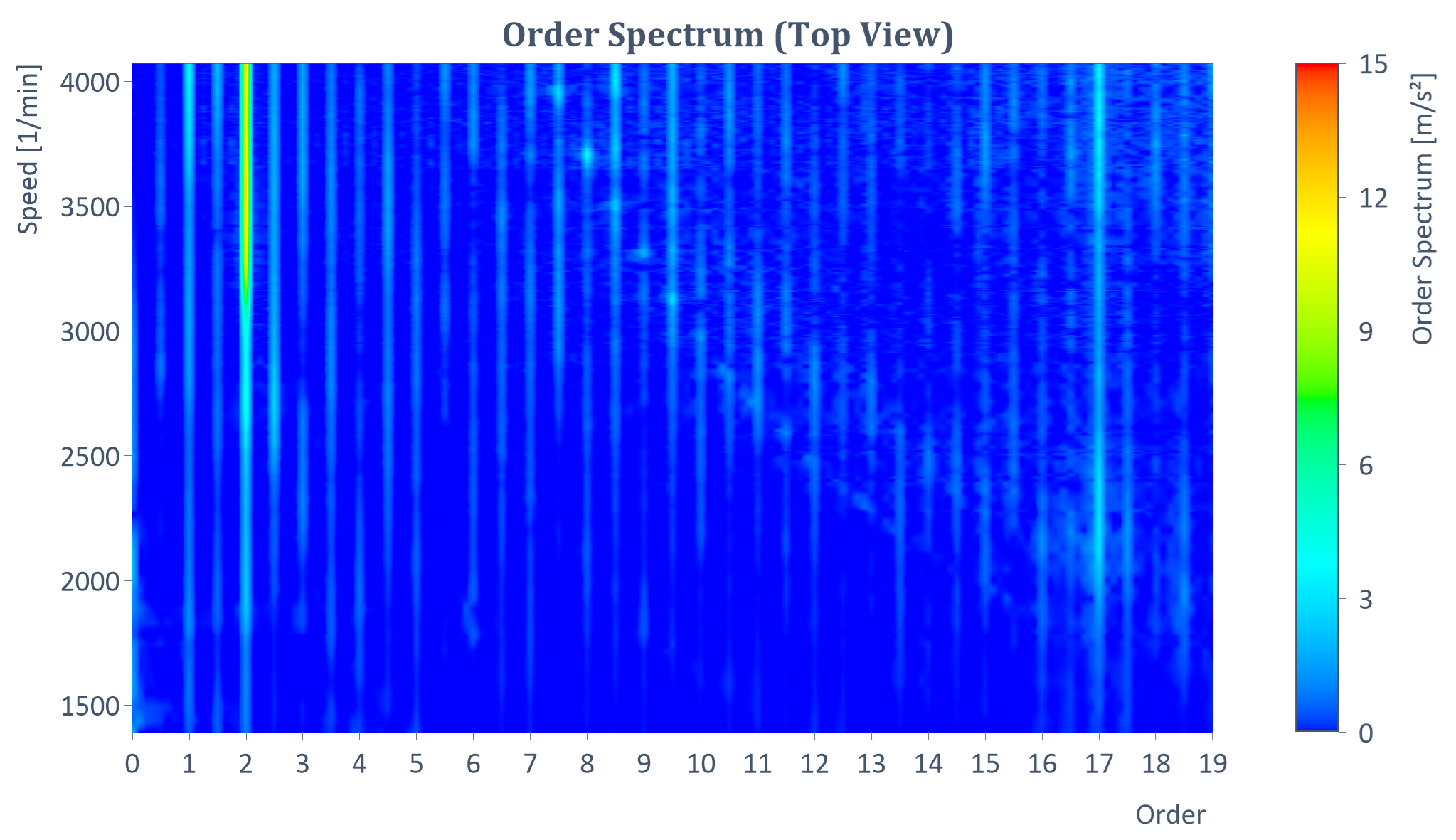
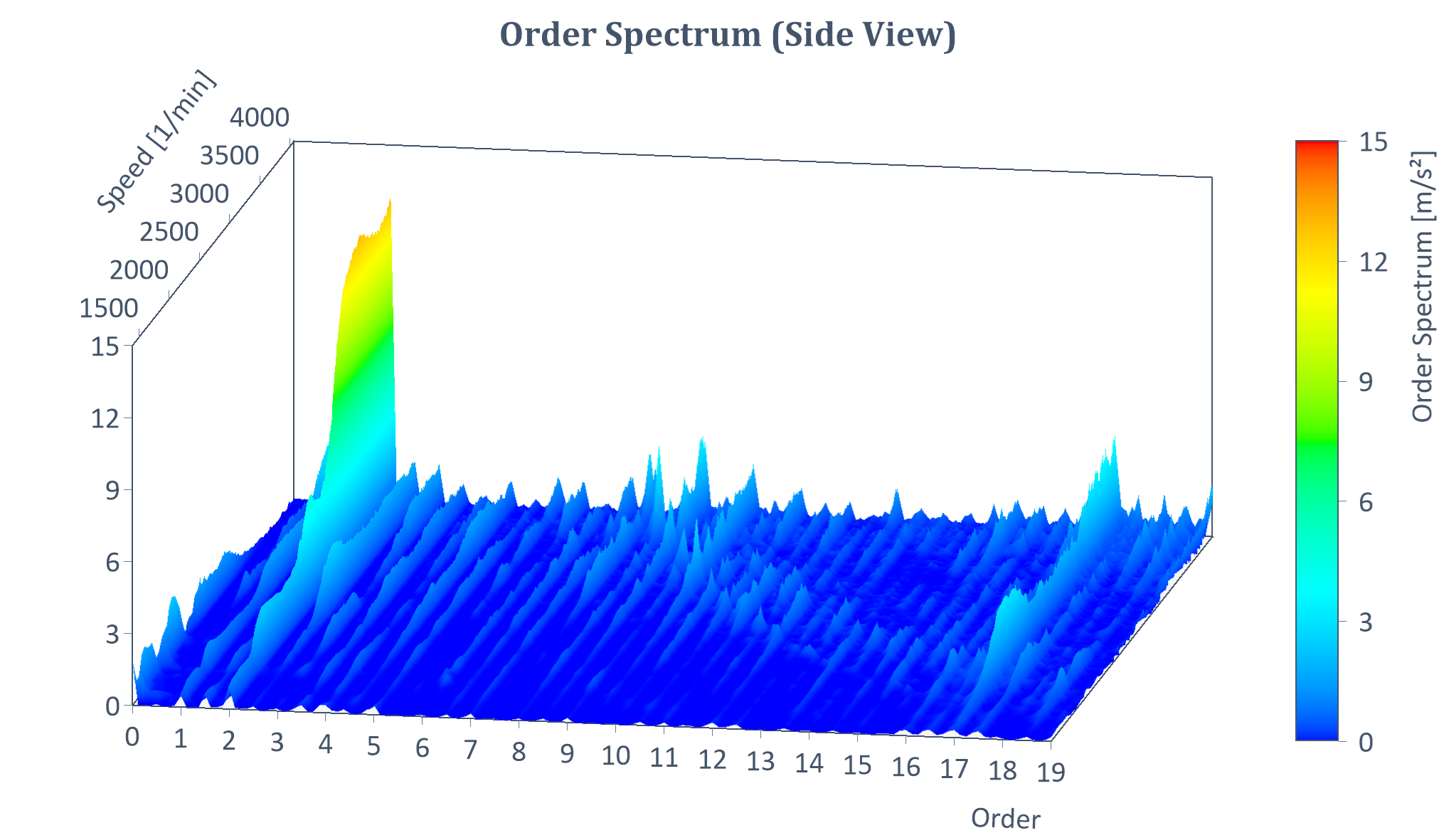
Ejemplo de espectro de órdenes RMS de unarampa de arranque (con Y = amplitud, X = orden, Z = velocidad de rotación):
Resultado de los cortes del orden (como lista)
Si se selecciona el modo de salida Extraer órdenes del espectro de órdenes (como lista) , se pueden seleccionar los siguientes tipos de resultados.
Resultado |
Descripción |
|---|---|
Y = amplitud, X = revolución |
Lista en la que cada elemento representa un orden extraído del espectro de órdenes. Los recorridos de amplitud de los órdenes se devuelven en función de las revoluciones. |
Y = amplitud, X = tiempo |
Lista en la que cada elemento representa un orden extraído del espectro de órdenes. Se devuelven las curvas de amplitud de los órdenes en función del tiempo. |
Y = amplitud, X = velocidad de rotación |
Lista en la que cada elemento representa un orden extraído del espectro de órdenes. Los recorridos de amplitud de los órdenes se devuelven en función de la velocidad de rotación. Se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
Y = amplitud, X = frecuencia (orden * velocidad de rotación) |
Lista en la que cada elemento representa un orden extraído del espectro de órdenes. Las curvas de amplitud de los órdenes se devuelven en función de la frecuencia (corresponde al producto del orden y la velocidad de rotación). Los puntos de resonancia se reconocen fácilmente en esta imagen porque ahora están superpuestos. También se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
Al calcular los cortes de orden en función de la velocidad de rotación, el resultado contiene puentes de velocidad de rotación no equidistantes (corresponden exactamente a los puentes de soporte de revolución equidistantes después de calcular el espectro de órdenes en el dominio de rotación). Por lo tanto, el resultado también puede analizarse en un rango de velocidades de rotación equidistantea con una velocidad inicial, una velocidad final y un incremento de velocidad de rotación por definir. Esto implica una interpolación lineal en función del rango de velocidad de rotación equidistante especificado. Para que el remuestreo lineal produzca resultados significativos, la resolución de velocidad calculada por el algoritmo debe ser suficientemente alta (por ejemplo, el mayor solapamiento posible en %de los segmentos de datos y/o una resolución del orden suficientemente baja).
Resultado de los cortes del orden (como serie de señales:)
Si se selecciona el modo de salida Extraer órdenes del espectro de órdenes (como serie de señales), se pueden seleccionar los siguientes tipos de resultados.
Resultado |
Descripción |
|---|---|
Y = amplitud, X = orden, Z = revolución |
Serie de señales en la que cada señal contiene las amplitudes para un valor de revolución específico en función de los órdenes extraídos. |
Y = amplitud, Z = orden, X = revolución |
Serie de señales en la que cada señal contiene las amplitudes de un orden extraído en función de las revoluciones. |
Y = amplitud, X = orden, Z = tiempo |
Serie de señales en la que cada señal contiene las amplitudes en un punto concreto del tiempo en función de los órdenes extraídos. |
Y = amplitud, Z = orden, X = tiempo |
Serie de señales en la que cada señal contiene las amplitudes de un orden extraído a en función de del tiempo. |
Y = amplitud, X = orden, Z = velocidad de rotación |
Serie de señales en la que cada señal contiene las amplitudes a una velocidad de rotación específica en función de los órdenes extraídos. Se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
Y = amplitud, Z = orden, X = velocidad de rotación |
Serie de señales en la que cada señal contiene las amplitudes de un orden extraído en función de la velocidad. Se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
Y = amplitud, X = orden, Z = Frecuencia (orden: * velocidad de rotación:) |
Serie de señales en la que cada señal contiene las amplitudes de un orden extraído en función de la frecuencia (corresponde al producto de orden y velocidad de rotación). Los puntos de resonancia se reconocen fácilmente en esta imagen porque ahora están superpuestos. También se puede ordenar de forma monótona ascendente según la velocidad de rotación. |
De la misma manera que se ha descrito anteriormente, el resultado puede analizarse en un rango de velocidades de rotación equidistantes al calcular los cortes de orden en función de la velocidad de rotación.
Órdenes y anchos de banda
Si se calculan los cortes de orden (o se utilizan para calcular los cortes de orden RMS promediados, véase más adelante), los órdenes que deben analizarse pueden establecerse explícitamente en una tabla o tomarse de un conjunto de datos. Para extraer estos órdenes del espectro de órdenes se dispone de los tres modos siguientes:
Modo de extracción |
Descripción |
|---|---|
Extraer órdenes como líneas sin ancho de banda |
Las curvas de órdenes (cortes de orden) se toman del espectro de órdenes sin ancho de banda. |
Extraer órdenes como máximo en la banda de orden (Peak-Hold) |
Las curvas de órdenes (cortes de orden) se toman del espectro de órdenes como máximo en la banda de orden. |
Extraer órdenes energéticamente en la banda de orden (RMS) |
Las curvas de órdenes (cortes de orden) se toman del espectro de orden RMS normalizado en potencia como niveles RMS (extracción energéticamente correcta). En concreto, el tipo de espectro siempre se establece en RMS y siempre se utiliza la normalización de potencia. |
Nota El tercer modo, es decir, la extracción energéticamente correcta mediante el cálculo del nivel RMS en la banda de orden establecida, suele utilizarse en la mayoría de las aplicaciones. Esta es la configuración típica para calcular los cortes de orden. El resultado corresponde claramente al recorrido RMS de la señal filtrada con paso banda en la banda de orden establecida. Por lo tanto, el mismo recorrido RMS del orden respectivo también puede calcularse alternativa y equivalentemente utilizando el objeto de análisis Filtro de órdenes.
Ejemplo de cortes de orden RMS (en forma de lista) de una rampa de arranque (con Y = amplitud, X = velocidad de rotación):
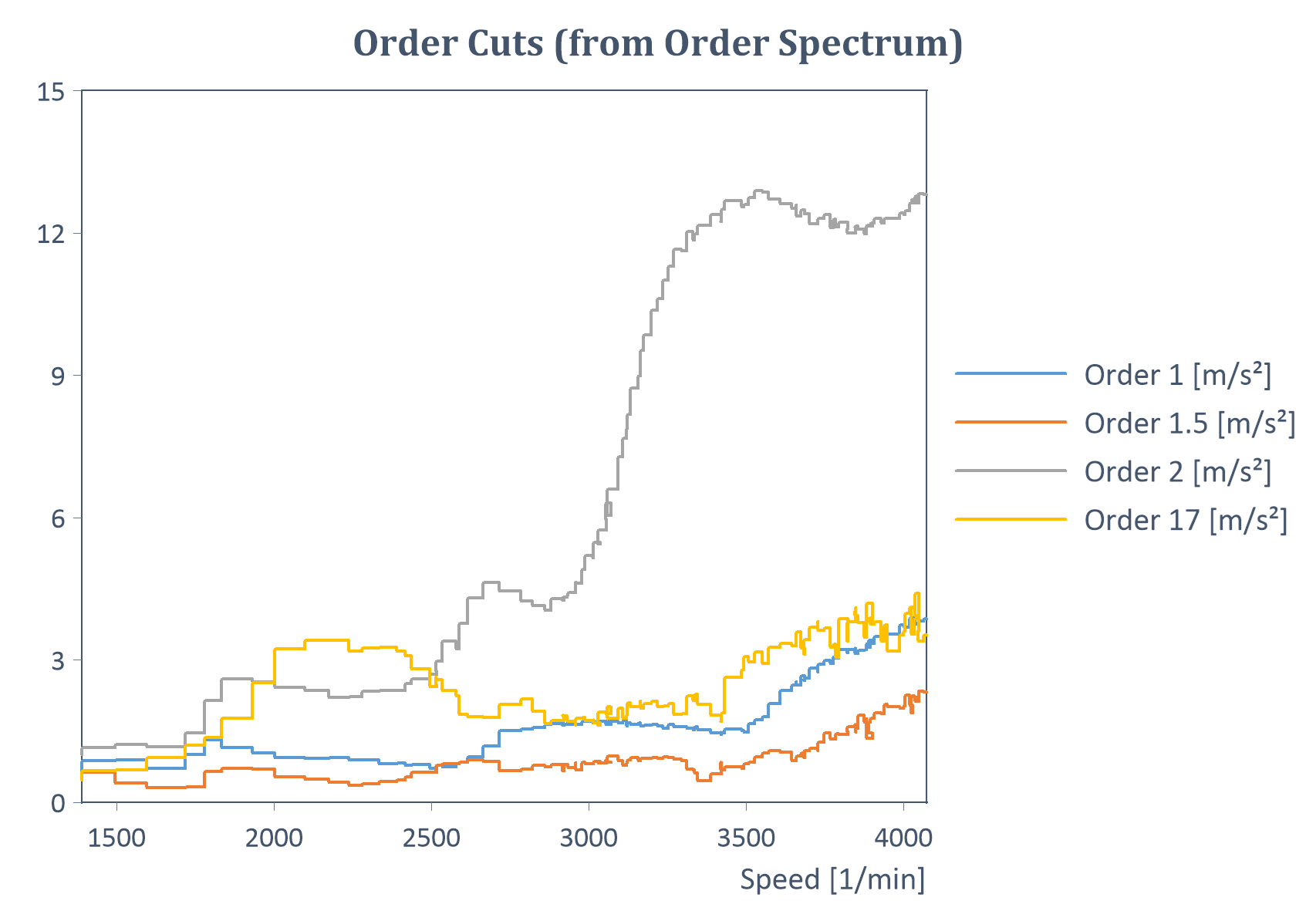
Resultado del análisis de órdenes RMS promediado
Al seleccionar el modo de salida Análisis de órdenes RMS promediado, se pueden seleccionar los siguientes tipos de resultados.
Resultado - análisis de órdenes RMS promediado |
Descripción |
|---|---|
Espectro de órdenes RMS promediado |
Calcula el valor medio aritmético en el espectro de órdenes RMS para cada orden (el tipo de espectro se establece siempre en RMS, en este caso). |
Cortes de orden RMS promediado |
Calcula la media aritmética de los cortes de orden RMS para cada orden (el tipo de espectro siempre se establece en RMS y siempre se utiliza la normalización de potencia). |
Ejemplo de espectro de órdenes RMS promediado de un análisis de órdenes con velocidad de rotación constante:
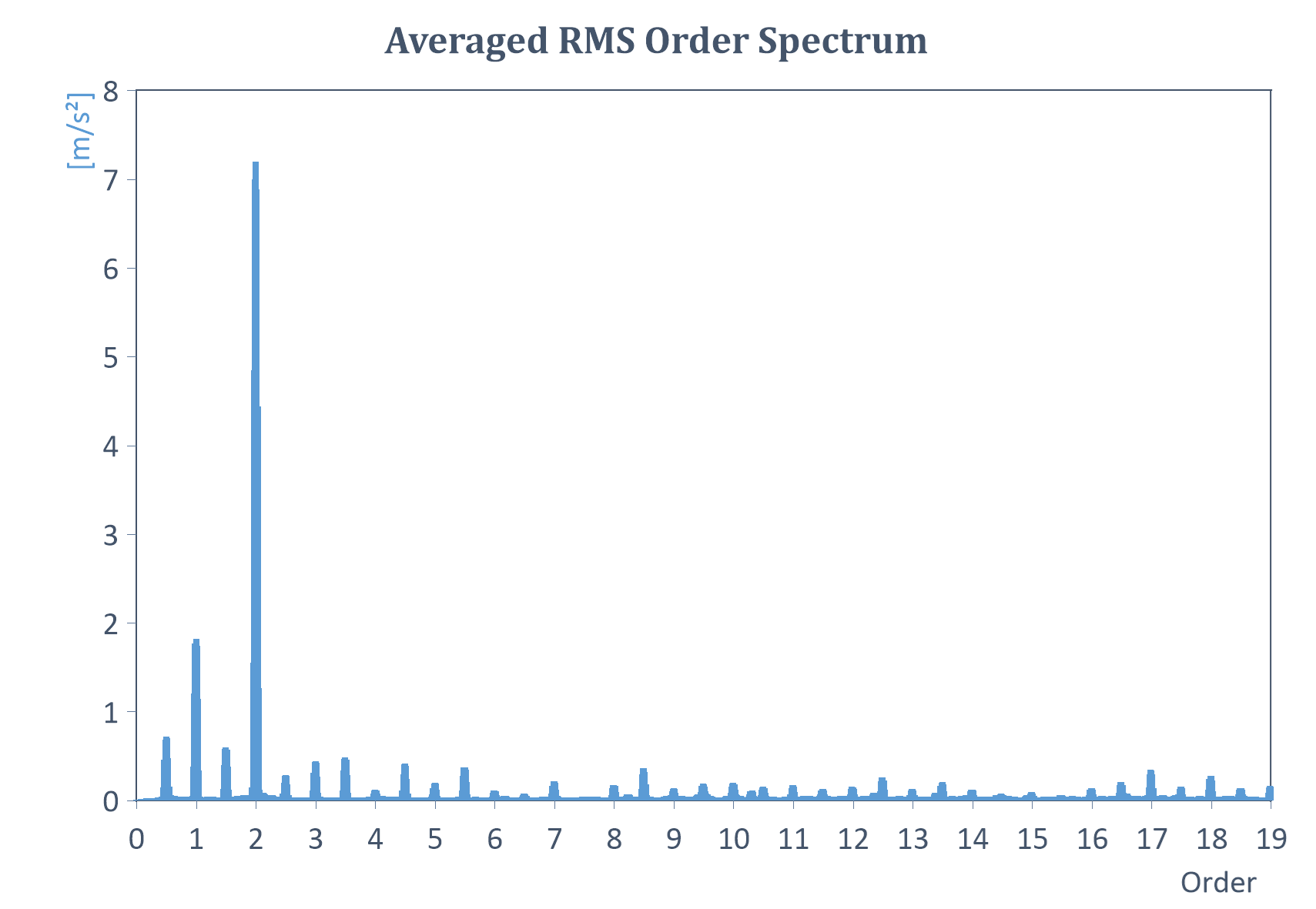
Ejemplo
En la base de datos del proyecto C:\Users\Public\Documents\Weisang\FlexPro\2025\Examples\Order Tracking Analysis.fpd o C:>Usuarios>Acceso público>Documentos públicos>Weisang>FlexPro>2025\Examples\Order Tracking Analysis.fpd encontrará ejemplos de los distintos casos de uso y modos en los que puede realizarse un análisis de órdenes. Se incluyen, en particular, los diagramas anteriores.
Función FPScript utilizada
Véase también
Objeto de análisis Filtro de órdenes
Objeto de análisis Muestreo sincronizado por revolución