Con este objeto de análisis se pueden calcular diversas variables, como tensiones principales o deformaciones principales, a partir de dos o tres señales de deformación medidas con una roseta de galgas extensométricas.
Una roseta de galgas extensométricas es una disposición de dos o más rejillas de galgas extensométricas próximas entre sí y con diferentes orientaciones, utilizada para medir las deformaciones normales en la superficie subyacente de un objeto de medición. En el caso de un estado de tensión biaxial cuyas direcciones principales se desconocen, bastan tres mediciones de deformación independientes entre sí en diferentes direcciones para determinar las deformaciones y tensiones principales.
Propiedades de la roseta
El cálculo es posible para los siguientes tipos de roseta:
Denominación |
Descripción |
|---|---|
Roseta en forma de T |
Dos rejillas perpendiculares entre sí; posición a y b; para obtener resultados correctos, la roseta en forma de T debe fijarse en la dirección de la tensión principal. |
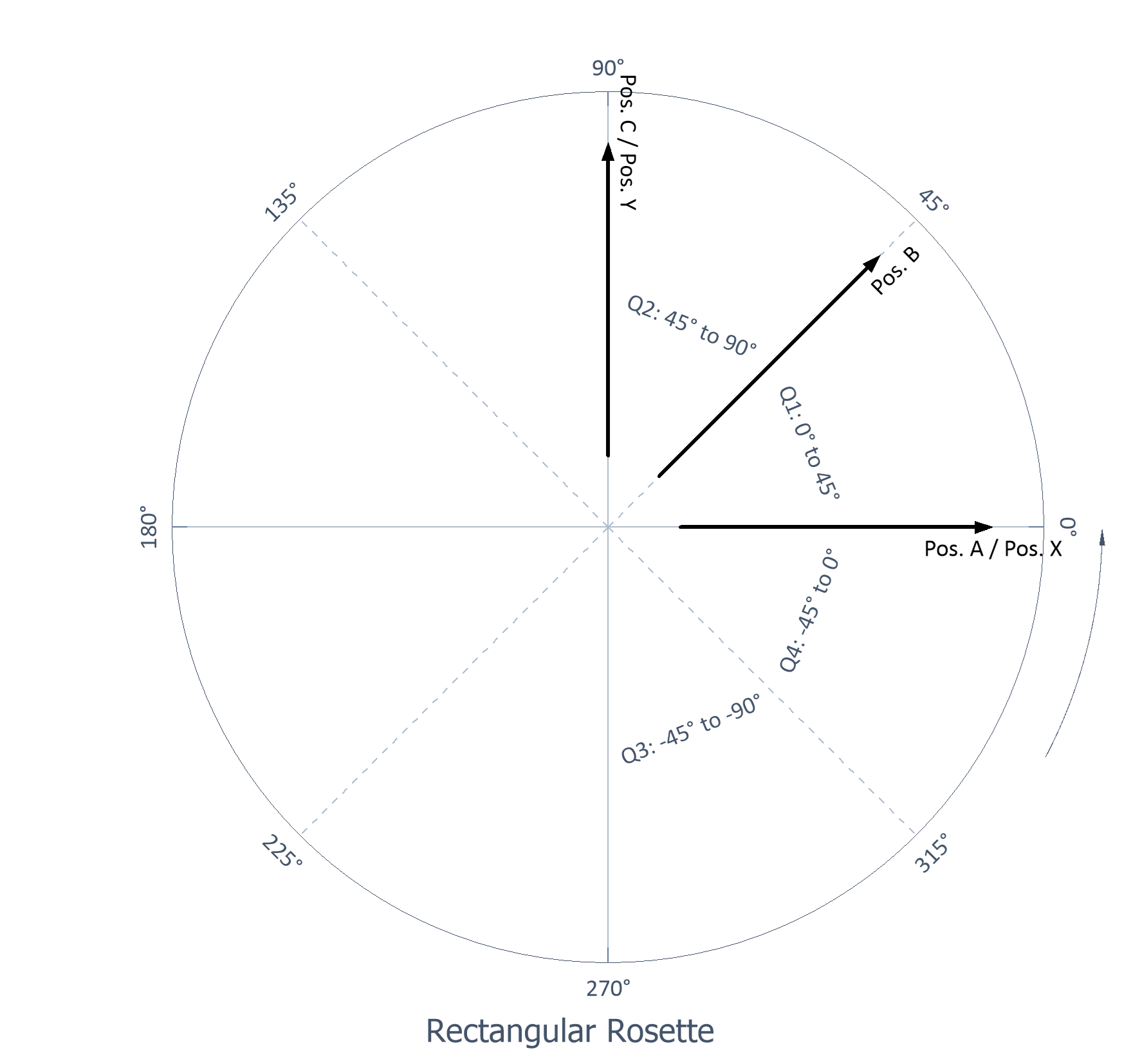
Roseta rectangular |
Tres rejillas con un espaciado de 45º |
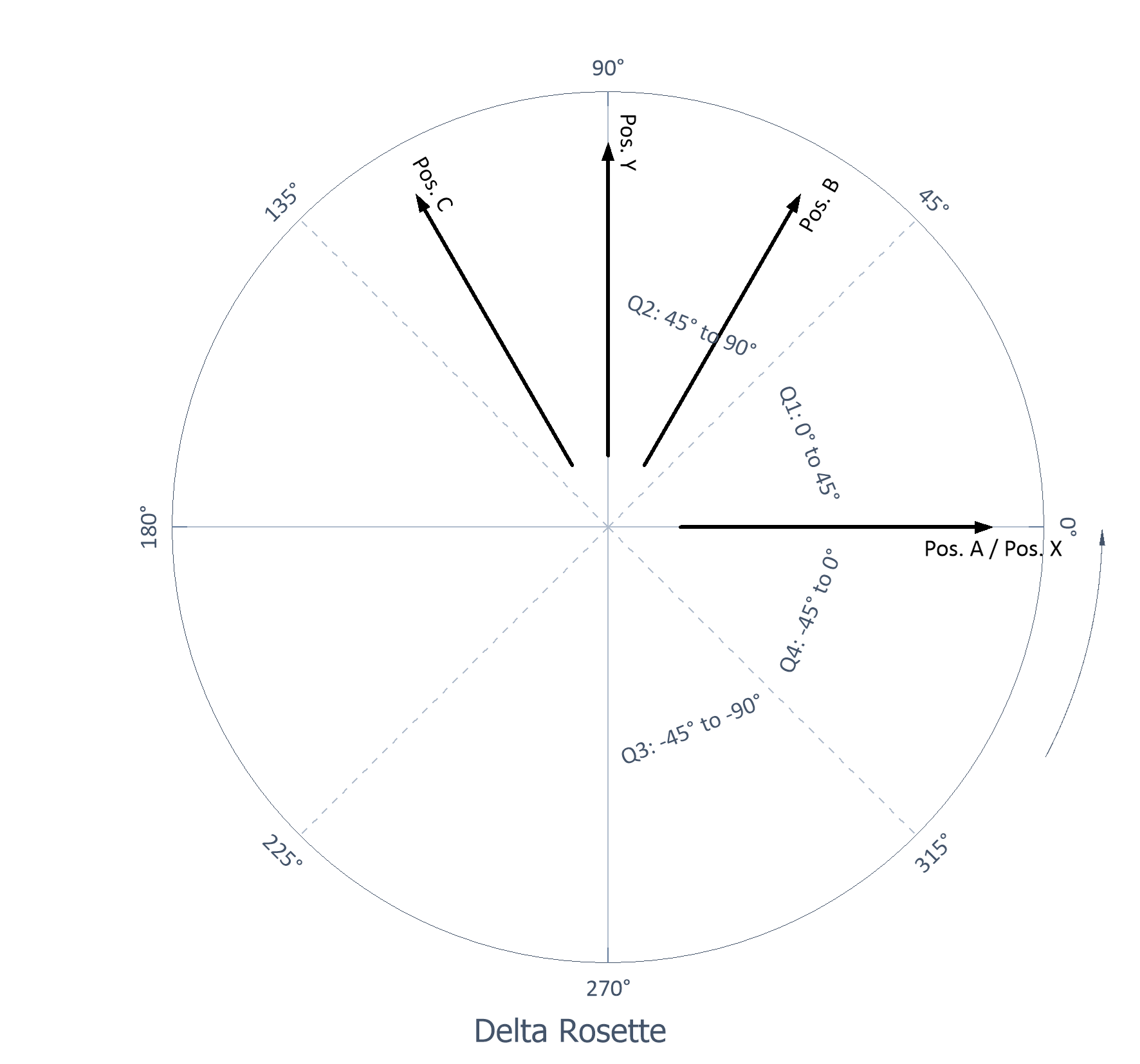
Roseta delta |
Tres rejillas con un espaciado de 60° o 120º |
Si el material del objeto de medición es homogéneo en su composición, se comporta de forma isótropa y presenta una relación tensión/deformación lineal, se puede aplicar la ley de Hook para el estado de tensión biaxial con el fin de calcular las tensiones principales a partir de las deformaciones principales. Para ello es necesario conocer el módulo de elasticidad E (módulo de Young) y el coeficiente de Poisson del material que se va a medir [1, 2].
Sensibilidad cruzada
El término sensibilidad transversal o sensibilidad a la deformación transversal se refiere a la reacción de las galgas extensométricas cuando actúan sobre ellas deformaciones transversales al eje longitudinal de la rejilla. Idealmente, es deseable que las galgas extensométricas sean totalmente insensibles a dichas deformaciones transversales. En la práctica, sin embargo, la mayoría de las galgas extensométricas son sensibles a la deformación transversal hasta cierto punto. Afortunadamente, la sensibilidad transversal de las galgas extensométricas de lámina modernas es muy baja y se sitúa en el orden de algunos puntos porcentuales de la sensibilidad a la deformación en la dirección de la rejilla. La magnitud de la sensibilidad a la deformación transversal depende de la aleación y geometría de la rejilla.
Se puede realizar una corrección matemática especificando la sensibilidad transversal [3]. Las señales de deformación corregidas pueden emitirse con el objeto de análisis y compararse así con las señales de deformación medidas.
Compensación de temperatura
Opcionalmente, se puede realizar una compensación de temperatura para las señales de deformación medidas. Se asume que se trata de galgas extensométricas autocompensadas, es decir, que la influencia de la resistencia del cable ya ha sido eliminada. Tampoco se tiene en cuenta la influencia de la temperatura en las cintas de conexión de las galgas extensométricas. El error residual se determina utilizando una función polinómica especificada en la hoja de datos de la galga extensométrica. Además de la función polinómica, la fórmula utilizada contiene términos para la dependencia de la temperatura del factor k y la desviación entre el coeficiente de dilatación térmica del material en el que se realizó la medición y el coeficiente de dilatación térmica del material de la rejilla de la galga extensométrica [4, 5].
Los coeficientes polinómicos se especifican como una serie de datos. El primer valor corresponde al coeficiente a0, el segundo valor al coeficiente a1, y así sucesivamente.
Para la compensación de la temperatura se utiliza la siguiente fórmula:
Denominación |
Símbolo |
|
|---|---|---|
Conjunto de datos de deformación |
εu(T) |
|
Conjunto de datos de temperatura |
T |
|
Coeficientes polinómicos |
a0, a1, a2, ... |
|
Temperatura de referencia |
TRef |
|
Factor k |
kD |
|
Coeficiente de dilatación del material |
αM |
|
Coeficiente de temperatura del factor k |
αk |
|
Coeficiente de expansión de la galga |
αSG |
Opciones de salida
Están disponibles las siguientes opciones de salida:
Denominación |
Descripción |
|
|---|---|---|
Deformación principal 1 |
Deformación principal 1 |
|
Deformación principal 2 |
Deformación principal 2 |
|
Tensión principal 1 |
Tensión principal en la dirección de la deformación principal 1 |
|
Tensión principal 2 |
Tensión principal en la dirección de la deformación principal 2 |
|
Ángulo |
Ángulo entre la dirección de la tensión principal máxima y la dirección X (especificado como un ángulo positivo en sentido antihorario entre 0° y 180°) |
|
Deformación por corte |
Deformación por corte en el sistema de coordenadas XY |
|
Tensión por corte |
Tensión por corte en el sistema de coordenadas XY |
|
Tensión máxima por corte |
Tensión máxima por corte |
|
Tensión equivalente según von Mises |
Tensión equivalente según von Mises |
|
Deformación X |
Deformación en dirección X (se corresponde con la deformación corregida en la posición a) |
|
Deformación Y |
Deformación en la dirección Y (se corresponde con la deformación en la posición a desplazada 90° en el sentido contrario a las agujas del reloj) |
|
Tensión X |
Tensión en la dirección de deformación X |
|
Tensión Y |
Tensión en la dirección de deformación Y |
|
Deformación corregida en la posición a |
Deformación corregida en la posición a con ayuda de la sensibilidad transversal |
|
Deformación corregida en la posición b |
Deformación corregida en la posición b con ayuda de la sensibilidad transversal |
|
Deformación corregida en la posición c |
Deformación corregida en la posición c con ayuda de la sensibilidad transversal |
Fórmulas de cálculo
Roseta perpendicular:
Denominación |
Fórmula |
|
|---|---|---|
Deformación principal 1 |
||
Deformación principal 2 |
||
Tensión principal 1 |
||
Tensión principal 2 |
||
Ángulo |
||
Deformación por corte |
0 |
|
Tensión por corte |
0 |
|
Tensión máxima por corte |
||
Tensión equivalente según von Mises |
||
Deformación X |
||
Deformación Y |
||
Tensión X |
||
Tensión Y |
||
Deformación corregida en la posición a, posición b |
Roseta rectangular:
Denominación |
Fórmula |
|
|---|---|---|
Deformación principal 1 |
||
Deformación principal 2 |
||
Tensión principal 1 |
||
Tensión principal 2 |
||
Ángulo |
||
Deformación por corte |
||
Tensión por corte |
||
Tensión máxima por corte |
||
Tensión equivalente según von Mises |
||
Deformación X |
||
Deformación Y |
||
Tensión X |
||
Tensión Y |
||
Deformación corregida en la posición a, posición b |
Roseta Delta:
Denominación |
Fórmula |
|
|---|---|---|
Deformación principal 1 |
||
Deformación principal 2 |
||
Tensión principal 1 |
||
Tensión principal 2 |
||
Ángulo |
||
Deformación por corte |
||
Tensión por corte |
||
Tensión máxima por corte |
||
Tensión equivalente según von Mises |
||
Deformación X |
||
Deformación Y |
||
Tensión X |
||
Tensión Y |
||
Deformación corregida en la posición a, posición b |
con
Bibliografía
[1] Micro-Measurements. Tech Note TN-515: Strain Gage Rosettes: Selection, Application and Data Reduction. Document Number: 11065, revisión 14-ago-2014.
[2] Karl Hoffmann. An Introduction to Stress Analysis using Strain Gauges. www.hbm.com
[3] Micro-Measurements. Tech Note TN-509: Errors Due to Transverse Sensitivity in Strain Gages. Document Number: 11059, revisión 28-jun-2011.
[4] Hottinger Baldwin Messtechnik GmbH. Technical Information T05414_01_E00_01: Temperature compensation of strain gauge ¼-bridges – Clear, brief and understandable
[5] Micro-Measurements. Tech Note TN-504-1: Strain Gage Thermal Output and Gage Factor Variation with Temperature. Document Number: 11054, revisión 14-ago-2014.
Funciones FPScript utilizadas
StrainGaugeTemperatureCompensation
* Este objeto de análisis no está disponible en FlexPro View y FlexPro Basic.