Puede utilizar este objeto de análisis para calcular la envolvente de un conjunto de datos (envolvente superior e inferior).
El objeto de análisis puede procesar series de datos, matrices de datos, señales, series de señales y listas.
Existen tres algoritmos para calcular las envolventes: Pendiente máxima, el Envolvente de picos y la Transformada de Hilbert:
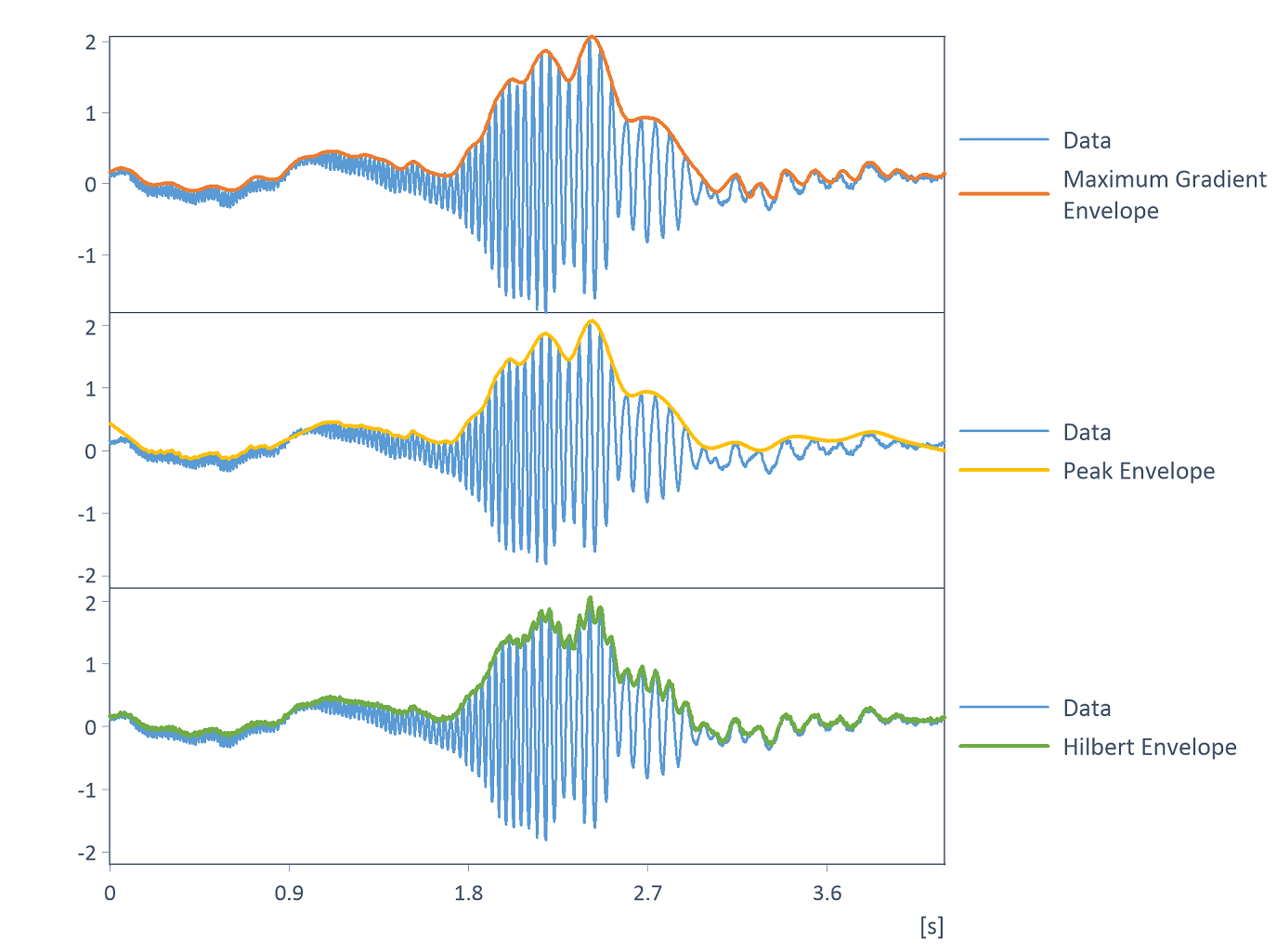
El algoritmo de Pendiente máxima se basa en las funciones UpperEnvelope o LowerEnvelope. Comenzando con el primer punto de datos, se calculan las conexiones rectilíneas con todos los vecinos de un intervalo y se determina su pendiente. El vecino con la pendiente más pequeña se convierte en el siguiente nodo de la curva envolvente y el algoritmo continúa con este valor. El Ancho de intervalo puede calcularse automáticamente o introducirse manualmente. Por lo tanto, la curva envolvente tiene menos puntos de datos que el conjunto de datos de entrada. Se puede utilizar la interpolación lineal para aumentar el muestreo del resultado hasta igualarla con la del muestreo del conjunto de datos de entrada. Como alternativa, los puntos de la curva envolvente pueden alisarse mediante la interpolación de spline.
El algoritmo Envolvente de picos calcula los puntos envolventes como puntos extremos locales (máximos o mínimos) utilizando la función Extrema. Se puede especificar la Histéresis para determinar los extremos. La histéresis es la cantidad mínima en la que la señal debe subir o bajar antes y después de un extremo para que el punto se acepte como extremo. Puede especificar la histéresis como valor absoluto o como porcentaje del rango del conjunto de datos. Otro parámetro que puede establecerse es si los puntos límite de la curva envolvente deben coincidir con los puntos límite del conjunto de datos de entrada, o bien extrapolarse. De forma similar al algoritmo de Pendiente máxima, el muestreo del resultado puede aumentarse hasta el muestreo del conjunto de datos de entrada mediante la interpolación lineal o la curva envolvente puede alisarse mediante la interpolación de spline.
El algoritmo Transformada de Hilbert calcula la envolvente utilizando la transformada de Hilbert. Esto proporciona una definición matemáticamente exacta de la envolvente como valor absoluto de la señal analítica calculada mediante la transformada de Hilbert (véase también Cálculo de la señal analítica). La transformada de Hilbert realiza internamente una transformada de Fourier (FFT) del conjunto de datos. La resolución de la FFT necesaria para el algoritmo se aumenta mediante el relleno de ceros (Zero-Padding), es decir, seleccionando una longitud de la FFT mayor que la longitud de los datos. Esto puede mejorar el resultado del cálculo. En el objeto de análisis, la longitud de la FFT puede aumentarse a la siguiente potencia de 2 si es necesario. Para las señales que tienen una tendencia u offset, también hay que eliminar previamente la tendencia para determinar la envolvente mediante la transformada de Hilbert. Las opciones de selección que se indican a continuación se corresponden con las opciones de selección para la eliminación de tendencias del objeto de análisis Análisis de señales:
Seleccionar |
Significado |
|---|---|
Constante |
Resta el valor medio del conjunto de datos. |
Lineal |
Resta la recta de mejor ajuste, es decir, la línea recta para la que la suma de los cuadrados de las desviaciones del conjunto de datos es mínima. |
Adaptativo |
Resta el valor medio de la curva envolvente superior e inferior. Esta configuración puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. |
media móvil |
Resta la media móvil. Se puede introducir el ancho de intervalo necesario para calcular la media móvil. Esta configuración puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. El filtro de media móvil es un filtro paso alto. |
Filtro de compensación de CC |
Filtro de paso alto para eliminar el desplazamiento de CC (filtro de paso alto IIR Butterworth). Se puede ajustar la frecuencia de corte y el orden (es decir, la pendiente) del filtro paso alto. El filtro puede utilizarse si la tendencia existente no es constante ni lineal, sino que depende del tiempo. |
Las configuraciones adecuadas para eliminar una tendencia dependiente del tiempo suelen ser la sustracción de la media móvil y el filtro de compensación de CC.
Funciones FPScript utilizadas
Véase también
Objeto de análisis Magnitud instantánea
Objeto de análisis Aislamiento de eventos
Objeto de análisis Interpolación de spline
* Este objeto de análisis no está disponible en FlexPro View.