Puede utilizar este objeto de análisis para realizar una interpolación de spline paramétrica de sus datos, es decir, para calcular la curva más lisa posible que conecte los puntos de su conjunto de datos. A diferencia de la interpolación de spline, la interpolación de spline paramétrica también permite interpolar curvas cuyos valores x no son estrictamente monótonos crecientes, por ejemplo, curvas de posición o líneas de contorno.
Para calcular la interpolación de spline paramétrica, FlexPro genera primero un conjunto de datos de parámetro T con valores estrictamente monótonos crecientes, que se deriva de los valores X e Y del conjunto de datos que se va a interpolar. A continuación, se realizan dos interpolaciones de spline, una para la función Y(T) y otra para la función X(T). Al igual que con la interpolación de spline normal, puede influir en la apariencia de la curva utilizando condiciones de contorno. Especifíquelos por separado para los márgenes de las funciones X(T) e Y(T).
El tipo determina la apariencia de la curva de spline en los márgenes. Los parámetros inicio X y final X se refieren a la interpolación de spline de la función X(T) e inicio Y y final Y se refieren a los de Y(T). La condición de contorno curvaturas en los márgenes igual a cero da como resultado splines paramétricos naturales, como se muestra en la siguiente imagen. Not-A-Knot significa que las 3.as derivadas de Y(T) y X(T) deben ser continuas en los márgenes.
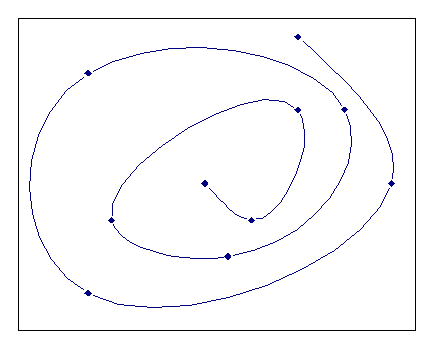
La interpolación de spline periódica y paramétrica genera curvas cerradas que no presentan dobleces en la unión. Sin embargo, el primer y el último punto de la curva deben coincidir. Si este no es el caso, FlexPro utiliza uno de dos procedimientos para forzar la periodicidad. Si selecciona Periódico, periodicidad por sustitución, se ignora el último punto del conjunto de datos y en su lugar se utiliza una copia del primer punto. Si se selecciona Periódico, periodicidad por adición, se añade una copia del primer punto al conjunto de datos si el último punto del conjunto de datos no es idéntico al primer punto.
La siguiente imagen muestra un ejemplo de splines paramétricos, periódicos:
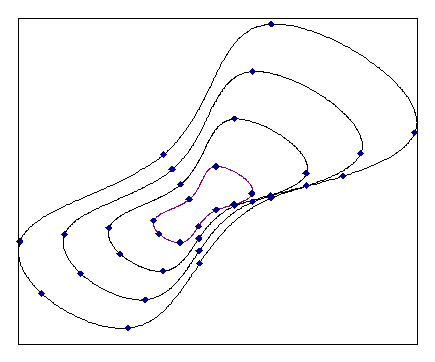
El resultado de la interpolación de spline es inicialmente un modelo matemático del conjunto de datos que se va a interpolar. El modo de evaluación especifica los puntos en los que se debe analizar la curva de spline calculada para obtener el conjunto de datos de resultado. Puede especificar si debe calcularse un conjunto de datos con un total de N puntos con el mismo espaciado (en relación con el conjunto de datos de parámetros T) o si cada intervalo T original debe dividirse en N partes.
Funciones FPScript utilizadas
Véase también
Objeto de análisis: interpolación de spline
* Este objeto de análisis no está disponible en FlexPro View.