Puede utilizar este objeto de análisis para realizar una interpolación de spline para sus datos, es decir, calcular una curva lo más suave posible que conecte los puntos de su conjunto de datos. La interpolación de spline está directamente integrada en el gráfico de líneas de FlexPro, por lo que solo necesitará este objeto de análisis si desea procesar matemáticamente los datos alisados.
La interpolación de spline conecta todos los puntos vecinos de la curva utilizando polinomios de tercer grado, es decir, funciones de la siguiente forma:
Dos polinomios se encuentran en un punto de la curva. El primer y el último punto de la curva son una excepción. Los coeficientes ai, bi, ci y di de los polinomios se eligen de modo que los polinomios vecinos coincidan en ubicación, pendiente y curvatura en los puntos donde se encuentran. Para el primer y el último punto, donde no se encuentran polinomios, puede influir en la apariencia de la curva spline mediante las llamadas condiciones de contorno, es decir, especifique la pendiente o la curvatura de la curva spline en los bordes izquierdo y derecho. Dependiendo del tipo de condiciones de contorno, obtendrá una apariencia diferente de la curva spline, como se muestra en la siguiente imagen:
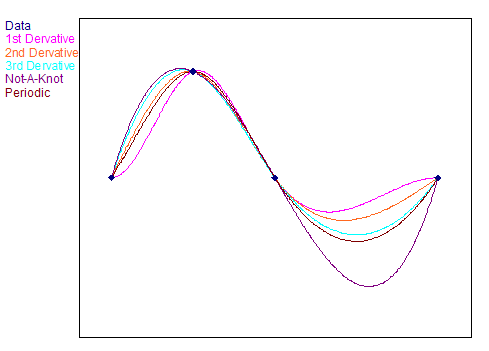
Cabe destacar lo siguiente:
•Splines naturales. Esto se obtiene si se seleccionan Curvaturas según especificación como condiciones de contorno y se introduce el valor cero como valor para las curvaturas en ambos bordes. La apariencia se corresponde con la curva que obtendría si uniera los puntos de la curva con una regla flexible.
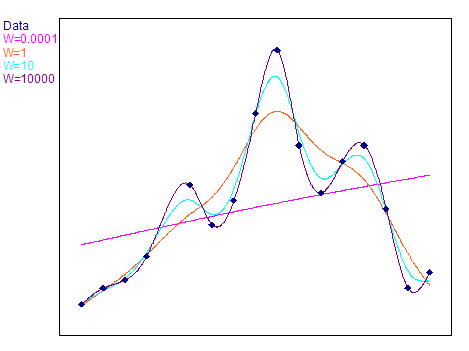
•Spline alisado. En este caso, la curva calculada no pasa necesariamente por los puntos de soporte especificados. La ondulación de la curva puede controlarse mediante un factor de ponderación. Si el factor de ponderación es próximo a cero, la recta de mejor ajuste con relación al error cuadrático es una curva de spline. Para un factor de ponderación muy grande, se obtendrá una curva spline natural, que corresponde a las condiciones de contorno especificadas anteriormente. En este caso, la curva spline sigue los puntos de la curva.
•Splines periódicos se crean con el requisito de que la pendiente y la curvatura de la curva spline coincidan en los bordes izquierdo y derecho. La curva spline resultante puede repetirse varias veces de forma consecutiva sin que aparezca un pliegue en las uniones. Para calcular una interpolación de spline periódica, el valor Y del primer y último punto deben coincidir. Si este no es el caso, FlexPro utiliza uno de dos procedimientos para forzar la periodicidad. Si selecciona Periódica, periodicidad por sustitución, se ignora el último valor Y del conjunto de datos y en su lugar se utiliza una copia del primer valor Y. Si se selecciona Periódica, periodicidad por adición, se añade una copia del primer valor Y al conjunto de datos si el último valor Y del conjunto de datos no es idéntico al primero. El valor X del último punto original más la diferencia entre el último y el penúltimo valor X se utiliza como valor X para este punto adicional.
•Splines con condición de contorno "Not-A-Knot". Estos utilizan dos polinomios idénticos en los bordes izquierdo y derecho, lo que corresponde a la condición de que la tercera derivada de las funciones spline en el segundo y penúltimo punto de datos sean continuas. Esto significa que estos puntos no son nodos reales de la curva spline.
El requisito previo para la interpolación de spline es que los valores x de los puntos sean estrictamente monótonos crecientes. Si no es el caso (por ejemplo, con una trayectoria), debe utilizar la Interpolación de spline paramétrica. Sin embargo, los valores X no tienen que ser equidistantes. Una vez calculados los coeficientes de la curva spline, FlexPro puede evaluar la función spline calculada en cualquier punto para obtener nuevos puntos de muestreo.
El siguiente gráfico muestra splines de compensación con distintos factores de ponderación:
El resultado de la interpolación de spline es inicialmente un modelo matemático del conjunto de datos que se va a interpolar. El Modo de muestreo especifica los puntos en los que se debe analizar la curva de spline calculada para obtener el conjunto de datos de resultado. Son posibles los siguientes modos de muestreo:
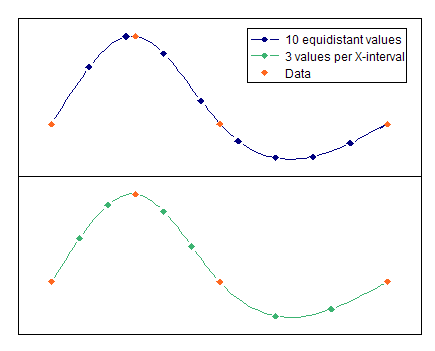
•N valores equidistantes: En este caso, la curva spline se analiza en N nodos equidistantes, independientemente de cómo se hayan distribuido previamente los valores X.
•N valores por intervalo X: En este caso, cada intervalo X anterior se divide en N intervalos iguales, en cuyos límites se analiza la función spline.
El siguiente gráfico muestra cómo funcionan los dos modos de evaluación:
Funciones FPScript utilizadas
Véase también
Objeto de análisis Interpolación de spline paramétrica
Objeto de análisis Interpolación lineal
* Este objeto de análisis no está disponible en FlexPro View.