MeshGrid

Crea una cuadrícula bidimensional. Útil para la visualización tridimensional de funciones con dos variables o funciones con argumentos de valores complejos.

Sintaxis

MeshGrid(X, Z)

La sintaxis de la función MeshGrid consta de los siguientes elementos:

Notas

El resultado siempre tiene la estructura de datos Lista.

La función genera una lista con dos entradas del mismo nombre, X y Z, a partir de dos series de datos: X, de longitud N, y Z, de longitud M. Sin embargo, las entradas resultantes de la lista son ahora matrices formadas por N filas y M columnas, que se crean replicando los argumentos de la función X o Z. Las unidades de las matrices resultantes coinciden con las unidades de los argumentos individuales.

El resultado puede interpretarse como una cuadrícula rectangular bidimensional con N x M puntos de cuadrícula del siguiente modo: Dadas, por ejemplo, la serie de datos X como {1, 2, 3, 4} en dirección horizontal y la serie de datos Z como {7, 8, 9} en dirección vertical. La cuadrícula, abarcada por X y Z, consta ahora de las coordenadas (1, 7), (2, 7), (3, 7), (4, 7), ..., (1, 9), (2, 9), (3, 9), (4, 9):

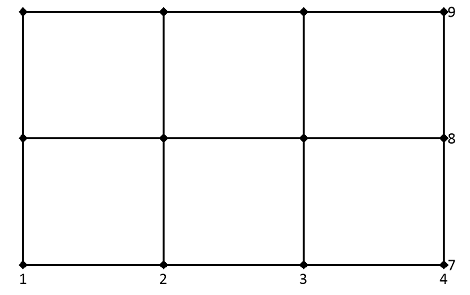
Por tanto, las coordenadas de cada punto de la cuadrícula se obtienen elemento por elemento a partir de las dos matrices del mismo nombre:

La función MeshGrid aplicada a las dos series de datos devuelve ahora la lista formada por las matrices representadas con el mismo nombre: X (primer elemento de lista) y Z (segundo elemento de lista).

La función suele utilizarse para la representación tridimensional de funciones y = f(x, z) de dos variables sobre una cuadrícula rectangular bidimensional. En particular, con ella pueden calcularse y representarse sobre el plano complejo las funciones y = f(z) = f(z1, z2) con argumentos de valores complejos z = z1 + i * z2.

Disponibilidad

FlexPro Basic, Professional, Developer Suite

Ejemplos

Dim x = {1, 2, 3, 4}
Dim z = {7, 8, 9}
Dim grid = MeshGrid(x, z)
Dim y = grid.["X"]^2 - grid.["Z"] // = grid.[0]^2 - grid.[1]
Signal(y, x, z)
 

Ejemplo 1: Procedimiento de cálculo de funciones con dos variables

Calcula la función y = x^2 - z en la cuadrícula abarcada por las series de datos {1, 2, 3, 4} (en la dirección X) y {7, 8, 9} (en la dirección Z):

Dim x = Series(-4, 4, 0.01)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = ArcTan2(grid.["Z"], grid.["X"])
Signal(y, x, z)
 

Ejemplo 2: Visualización de la función ArcTan2 con 2 variables

Calcula la función ArcTan2 y = f(x, z) = ArcTan2(z, x) sobre el rango (x, z) bidimensional [-4, 4] x [-4, 4]. La visualización en un diagrama de contorno 3D proporciona:

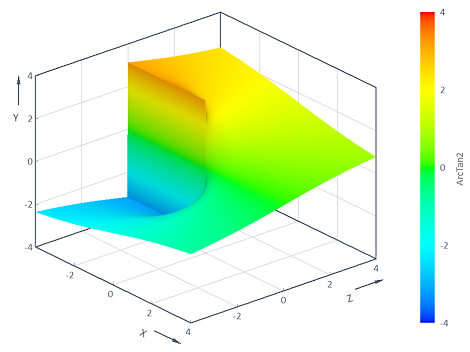
Dim x = Series(-16, 16, 0.04)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = Sinc(Sqrt(grid.["X"]^2 + grid.["Z"]^2))
Signal(y, x, z)
 

Ejemplo 3: Visualización de la función Sinc en 2D

Calcula la función Sinc bidimensional y = f(x, z) = Sinc(Sqrt(x^2 + z^2)) sobre el área bidimensional (x, z)[-16, 16] x [-16, 16]. La visualización en un diagrama de contorno 3D proporciona:

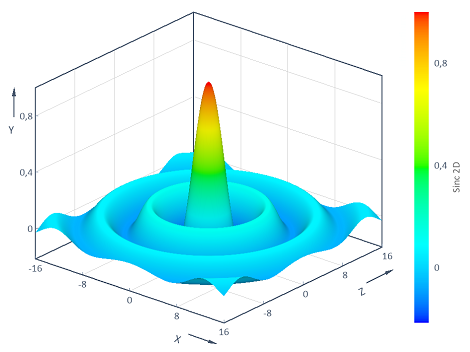
Dim z1 = Series(-6, 6, 0.02)
Dim z2 = z1
Dim grid = MeshGrid(z1, z2)
Dim y = Real(Log(grid.[0] + 1i * grid.[1]))
Signal(y, z1, z2)
 

Ejemplo 4: Visualización de funciones con argumentos complejos

Calcula la parte real del logaritmo complejo y = f(z1, z2) = Real(Log(z1 + i* z2)) en el plano complejo (z1, z2)[-6, 6] x [-6, 6]. La visualización en un diagrama de contorno 3D proporciona:

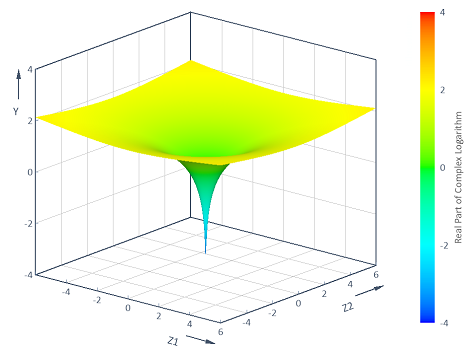
Arguments x, z
Dim xMatrix = x # NumberOfRows(z)
Dim zMatrix = TransposeMatrix(z # NumberOfRows(x))
List("X", xMatrix, "Z", zMatrix)
 

Ejemplo 5: Código FPScript equivalente

Esta función FPScript devuelve el mismo resultado que la función MeshGrid.

Véase también

Función ArcTan2

Función List

Función NumberOfColumns

Función NumberOfRows

Función Reshape

Función Shape

Función TransposeMatrix

Operador de lista

Operador de elemento de lista