Interpola un conjunto de datos bidimensional a través de una cuadrícula de curvas spline y los muestrea en puntos predefinidos.
Sintaxis
Spline2D(Surface, NX, NZ, SamplingMode, [ VX1 = 0 ], [ VXn = 0 ], [ VZ1 = 0 ] [ , VZn = 0 ])
o
Spline2D(DataMatrix, LocusX, LocusZ, NX, NZ, SamplingMode, [ VX1 = 0 ], [ VXn = 0 ], [ VZ1 = 0 ] [ , VZn = 0 ])
La sintaxis de la función Spline2D consta de los siguientes elementos:
Parte |
Descripción |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Surface |
La matriz de datos o la serie de señales con componente Z con un intervalo de muestreo constante, que se interpola. Si faltan los componentes X y Z, se generan automáticamente. Las estructuras de datos permitidas son Matriz de datos y Serie de señales. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||||||||||||
DataMatrix |
Matriz de datos con el componente Y de la serie de señales que se va a interpolar. Si especifica una serie de señales, se utiliza su componente Y. Las estructuras de datos permitidas son Matriz de datos y Serie de señales. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
LocusX |
Serie de datos con el componente X de la serie de señales que se va a interpolar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
LocusZ |
Serie de datos con el componente Z de la serie de señales que se va a interpolar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
NX |
Especifica el número total de puntos o por intervalo X de la señal. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 0. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
NZ |
Especifica el número total de puntos o por intervalo Z de la señal. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 0. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
SamplingMode |
Especifica cómo debe muestrearse la curva spline calculada y qué condiciones de contorno deben utilizarse. El argumento SamplingMode puede tener los siguientes valores:
...más una constante que determina las condiciones de contorno.
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||
VX1 |
Determina la condición de contorno en el borde izquierdo. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos reales. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 0 si no se especifica el argumento. |
||||||||||||||||
VXn |
Determina la condición de contorno en el borde derecho. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos reales. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 0 si no se especifica el argumento. |
||||||||||||||||
VZ1 |
Determina la condición de contorno en el borde posterior. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos reales. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 0 si no se especifica el argumento. |
||||||||||||||||
VZn |
Determina la condición de contorno en el borde frontal. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos reales. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 0 si no se especifica el argumento. |
Notas
El resultado es siempre el tipo de datos En coma flotante de 64 bits.
En primer lugar, se modela una curva spline para cada fila de la cuadrícula abarcada por el componente Y del conjunto de datos y se evalúa en las posiciones Z deseadas. Una curva spline de este tipo está formada por polinomios cúbicos unidos entre sí de forma que la curva sea lo más suave posible. A continuación, se modela una curva spline para cada columna de la matriz de datos calculada y se evalúa en las posiciones X deseadas. Antes de cada interpolación de spline, los valores no válidos de las filas o columnas se eliminan mediante interpolación lineal. El componente Y del conjunto de datos que se va a interpolar debe contener al menos 3 x 3 valores y los componentes X y Z deben ser estrictamente monótono creciente.
Puede obtener una curva spline natural con V1 y Vn como 2.ª derivadas son iguales a cero.
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
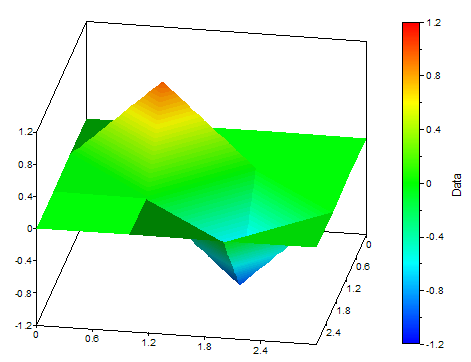
Dim data = {{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}
Spline2D(data, 100, 100, SPLINE_EQUIDISTANT + SPLINE_NOTAKNOT)
Interpola la matriz a través de una cuadrícula de curvas spline sin condiciones de contorno.
Los siguientes gráficos muestran una curva spline 2D y los datos subyacentes:
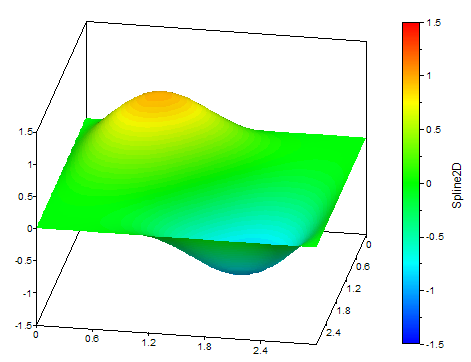
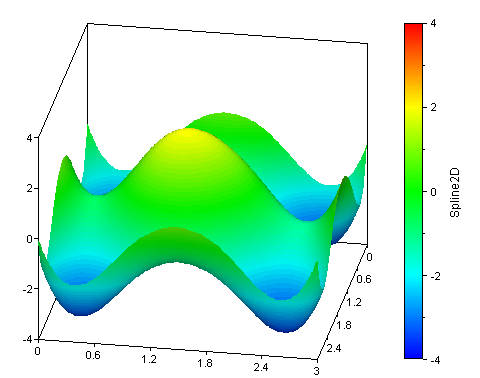
Spline2D(data, 100, 100, SPLINE_EQUIDISTANT + SPLINE_1DERIVATIVE, -10, 10, -10, 10)
Interpola la matriz con las condiciones de contorno. VX1, VZ1, VXn y VZn se interpretan como pendiente (1.ª derivada) en el primer y último punto en las direcciones X y Z respectivamente.
Véase también
Objeto de análisis Interpolación de spline
Objeto de análisis Interpolación de superficie
Objeto de análisis Aproximación 2D
Bibliografía
[1] "Carl de Boor": "A Practical Guide to Splines, Revised Edition". "Springer-Verlag, New York", 2001. ISBN 0-387-95366-3.