Determina una o varias isolíneas a partir de una matriz de datos o una serie de señales.
Sintaxis
Isoline(DataSet, Level [ , Result = ISOLINE_2D ])
La sintaxis de la función Isoline consta de los siguientes elementos:
Parte |
Descripción |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
El conjunto de datos para el que debe calcularse la isolínea. Las estructuras de datos permitidas son Matriz de datos y Serie de señales. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||
Level |
Especifica el valor del nivel para el que debe calcularse la isolínea. Las estructuras de datos permitidas son Valor escalar y Serie de datos. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||
Result |
Determina el resultado de la función. El argumento Result puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado ISOLINE_2D si no se especifica el argumento. |
Notas
Una isolínea está formada por la intersección de la superficie especificada por los datos y un plano horizontal. El resultado es una señal o una curva espacial, en función del parámetro Result. Si se especifica una serie de datos para el parámetro Level, se calculan varias isolíneas y se devuelven en forma de lista. La isolínea de un plano determinado puede estar formada por varias curvas parcialmente cerradas. A continuación, se separan en el resultado mediante un valor inválido. Puede optimizar la visualización desactivando la opción Puenteo de valores inválidos para la curva del diagrama.
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
Isoline(Surface, 100)
Devuelve la isolínea del nivel 100 como señal.
Isoline(Surface, 100, ISOLINE_3D)
Devuelve la isolínea del nivel 100 como curva espacial.
Dim Surface = {{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}
Surface = Spline2D(Surface, 100, 100, SPLINE_EQUIDISTANT + SPLINE_1DERIVATIVE, -10, 10, -10, 10)
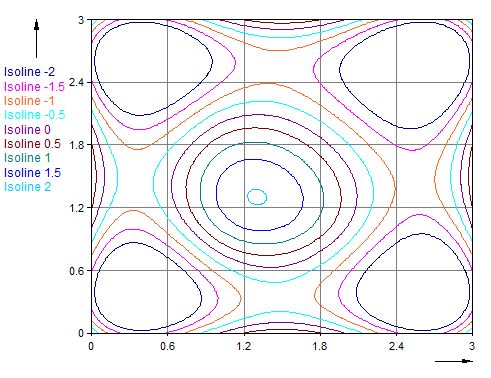
Isoline(Surface, Series(-2, 2, 0.5))
La resolución de la isolínea corresponde a la resolución de la matriz transferida. Cuando solo se dispone de pocos puntos de cuadrícula, se recomienda realizar una interpolación previa. En este ejemplo se interpola la matriz mediante una cuadrícula de curvas spline y, posteriormente, se calculan isolíneas para los niveles predefinidos.
El siguiente gráfico muestra el resultado: