Calcula la derivada de un conjunto de datos con un filtro de alisado Savitzky-Golay (derivada por mínimos cuadrados). Procedimiento eficaz para determinar la derivada alisada de un conjunto de datos ruidosos.
Sintaxis
SavitzkyGolayDerivative(DataSet, SmoothingWidth, [ PolynomialOrder = 4 ], [ DerivativeOrder = 1 ] [ , Extrapolate = FALSE ])
La sintaxis de la función SavitzkyGolayDerivative consta de los siguientes elementos:
Parte |
Descripción |
|---|---|
DataSet |
El conjunto de datos (ruidosos) cuya derivada (alisada) debe calcularse. Se permiten todas las estructuras de datos excepto Valor escalar y Lista. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
SmoothingWidth |
Especifica cuántos valores vecinos, incluyendo el punto de datos respectivo, deben incluirse en el cálculo del filtro de derivada (alisada). El ancho de alisado debe ser un número impar. De lo contrario, el intervalo es asimétrico y se incluye en el cálculo un valor más a la derecha del centro que a la izquierda. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 0. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
PolynomialOrder |
Especifica el orden del polinomio que se ajusta localmente al conjunto de datos y que, por tanto, se utiliza para determinar los coeficientes del filtro de derivada (alisada). El orden del polinomio debe ser menor que el ancho de alisado (para que haya suficientes puntos de datos disponibles para el ajuste polinómico local). En caso contrario, el orden del polinomio para el cálculo se reduce a SmoothingWidth - 1. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 1 y menor o igual que 15. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 4 si no se especifica el argumento. |
DerivativeOrder |
Especifica el orden de la derivada deseada. El argumento no debe ser mayor que PolynomialOrder. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 1 y menor o igual que 15. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado 1 si no se especifica el argumento. |
Extrapolate |
El valor TRUE indica que los puntos de borde se extienden simétricamente para el filtrado. En este caso, los coeficientes del filtro solo tienen que calcularse una vez. Aunque la extrapolación puede provocar un comportamiento irregular de la derivada (alisada) en los bordes, el algoritmo sigue siendo rápido. Si se selecciona FALSE, se utiliza el mismo orden polinómico para determinar la derivada (alisada) en los puntos de borde. El ancho de alisado y el orden del polinomio que se va a ajustar siguen siendo los mismos en los puntos de bordes, mientras que el centro del filtro se desplaza hacia los bordes. En este caso, los coeficientes del filtro deben calcularse individualmente para todos los puntos de borde. Esto suele proporcionar una mayor precisión para determinar la derivada (alisada) en los puntos de borde, pero el algoritmo es considerablemente más lento. Las estructuras de datos permitidas son Valor escalar. Los tipos de datos permitidos son Valor booleano. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado FALSE si no se especifica el argumento. |
Notas
El resultado tiene la misma estructura y unidad que el argumento DataSet.
Para calcular la derivada (alisada), cada valor en DataSet se pondera con (SmoothingWidth-1)/2 valores vecinos a la izquierda y (SmoothingWidth-1)/2 valores vecinos a la derecha (si SmoothingWidth es impar). La derivada (alisada) equivale a una convolución de la señal con coeficientes de filtro de longitud SmoothingWidth. En este procedimiento, los coeficientes del filtro se determinan de forma que el resultado sea la derivada de una regresión polinómica local (es decir, un ajuste de curva polinómico local). Los coeficientes del filtro no dependen de los valores Y. El algoritmo se describe en Algoritmo SavitzkyGolay.
El filtrado no está optimizado para la supresión de las frecuencias más altas, sino para la supresión de los momentos estadísticos de orden superior. Por lo tanto, el filtro es especialmente adecuado para determinar la derivada de señales que tendrían un alto rango de frecuencias sin ruido. El método de alisado Savitzky-Golay también se denomina "Digital Smoothing Polynomial Filter (DISPO)" o "Least-Squares Smoothing" o "Least-Squares Differentiation".
Los valores se convierten en números en coma flotante de 64 bits reales o complejos antes del filtrado. El tipo de datos del resultado siempre es número en coma flotante de 64 bits real o complejo.
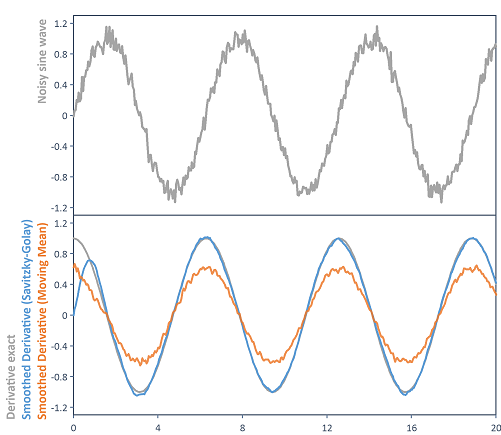
El gráfico destaca la diferencia de la Derivative alisada posteriormente con la función Smooth (media móvil), y la función SavitzkyGolayDerivative (con orden polinómico 7). Se utiliza el mismo ancho de alisado en cada caso. El filtro de derivada Savitzky-Golay puede aproximarse a la curva bastante mejor que la media móvil:
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
SavitzkyGolayDerivative(Signal, 11, 3)
Calcula la primera derivada alisada de una señal ruidosa con el filtro Savitzky-Golay. La derivada se calcula determinando la derivada de un polinomio de tercer grado, que se ajusta localmente al conjunto de datos. Para el ajuste de curva local, se incluyen en el resultado un total de 11 valores, es decir, cinco valores vecinos a la izquierda y cinco a la derecha de cada punto de datos.
SavitzkyGolayDerivative(Signal, 25, 6, 2)
Calcula la segunda derivada alisada de una señal ruidosa con el filtro Savitzky-Golay. La segunda derivada se calcula determinando la derivada de un polinomio de sexto grado, al que se ajustan localmente 25 puntos de datos.
SavitzkyGolayDerivative(DataSet, 5, 4)
Calcula la primera derivada determinando la derivada de un polinomio de cuarto grado, que al que se ajustan localmente 5 puntos de datos. El polinomio de cuarto grado ajustado a 5 puntos de datos está unívocamente determinado y coincide con el polinomio de interpolación de Lagrange. Por tanto, el resultado del cálculo es: Derivative(DataSet, DERIVATIVE_CENTRAL_5_POINTS).
Dim N = 6
Dim polyOrder = 6
Dim width = 2*N + 1
Dim dirac = (0 # width) : 1 : (0 # width)
Dim coeff = SavitzkyGolayDerivative(dirac, width, polyOrder, 1)[N+1, N+ width]
AmplitudeResponse(coeff)
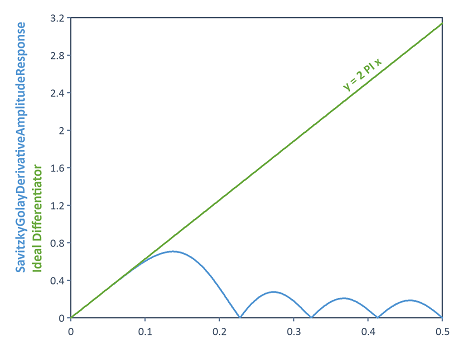
Calcula la respuesta de amplitud del filtro de derivada Savitzky-Golay (para orden polinómico 6 y ancho de alisado 13). Para ello, se aplica la función SavitzkyGolayDerivative a un impulso de Dirac. Así se obtiene la función de transferencia del sistema en forma de coeficientes de filtro. Utilizando los coeficientes de filtro, se puede calcular la respuesta de amplitud del filtro mediante la función AmplitudeResponse.
Véase también
Objeto de análisis Análisis de señales
Bibliografía
[1] Savitzky, A.; Golay, M.J.E.: Smoothing and Differentiation of Data by Simplified Least Squares Procedures. En: Analytical Chemistry, Vol. 36, No. 8, Pages 1627-39. http://pubs.acs.org/doi/abs/10.1021/ac60214a047, 1964.
[2] A. Gorry: General least-squares smoothing and differentiation by the convolution (Savitzky–Golay) method. En: Analytical Chemistry, Vol. 62, No. 2, Pages 570-3. http://pubs.acs.org/doi/abs/10.1021/ac00205a007, 1990.