Determina los cuantiles individuales, móviles o de bloque de un conjunto de datos.
Sintaxis
Quantile(DataSet, Alpha, [ Mode = PROCESS_COLUMNS ] [ , IntervalWidth ])
La sintaxis de la función Quantile consta de los siguientes elementos:
Parte |
Descripción |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
El conjunto de datos que se va a evaluar. Todas las estructuras de datos están permitidas. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||||||||||
Alpha |
Especifica el parámetro para determinar el cuantil. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos numéricos. El valor debe ser mayor o igual que 0 y menor o igual que 1. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||
Mode |
Especifica cómo deben procesarse las matrices de datos y las series de señales y si deben determinarse cuantiles individuales, móviles o de bloque. Si omite el argumento, los cuantiles individuales se determinan columna por columna. El argumento Mode puede tener los siguientes valores:
...más una constante opcional que determina el método de cálculo:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado PROCESS_COLUMNS si no se especifica el argumento. |
||||||||||||||
IntervalWidth |
Este argumento es necesario para determinar los cuantiles móviles y de bloque. A continuación, el ancho del intervalo especifica el número de valores que se deben tener en cuenta. El ancho debe ser un número impar. De lo contrario, el intervalo es asimétrico y se incluye en el cálculo un valor más a la derecha del centro que a la izquierda. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros. El valor debe ser mayor o igual que 1. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
Notas
Para determinar el cuantil alpha, se ordena la muestra y, a continuación, se extrae el valor en la posición Alpha * NumberOfRows(DataSet).
Si Alpha especifica una posición que se encuentra entre dos valores vecinos (por ejemplo, número par de valores y Alpha = 0,5), se produce una interpolación lineal entre los valores. Existen términos especiales para los siguientes valores de Alpha:
Valor de Alpha |
Interpretación |
|---|---|
0.25 |
Cuartil inferior |
0.5 |
Mediana |
0.75 |
Cuartil superior |
Se devuelve un valor escalar sin cambios. En el caso de señales y series de señales, se procesa el componente Y y, si es posible, se adopta el componente X o Z. Al calcular cuantiles móviles y de bloque, la estructura de datos del resultado corresponde a la del argumento. Si, por el contrario, DataSet es una serie de datos o una señal, el resultado es un valor escalar con el cuantil buscado. En cualquier otro caso, el resultado es una serie de datos o una señal con un cuantil por columna o fila.
Los tipos de datos de tiempo de calendario y de intervalo de tiempo se conservan en el resultado. Para todos los demás tipos de datos, el resultado tiene el tipo número en coma flotante de 64 bits.
La función Quantile es adecuada para realizar un filtro de mediana. Para ello, utilice la función con Alpha = 0,5 y en modo CALC_MOVING. Un filtro de mediana suaviza una señal de forma similar a una media móvil, pero muestra un mejor comportamiento con señales con valores atípicos. Los valores atípicos individuales influyen mucho en la media, pero poco en la mediana. El siguiente gráfico muestra las diferencias:
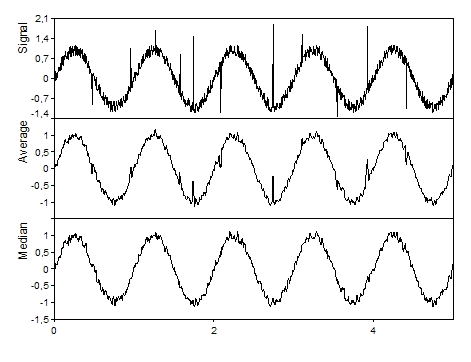
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
Quantile({2, 5, 7, 1, 3}, 0.5) |
Devuelve 3. (la mediana) |
Quantile(Signal, 0.5, CALC_MOVING, 10) |
Filtrado de mediana con ancho de alisado 10. |