Calcula diversas funciones de distribución o densidad.
Sintaxis
Distribution(X, Distribution, Parameter1 [ , Parameter2 ])
La sintaxis de la función Distribution consta de los siguientes elementos:
Parte |
Descripción |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
X |
Contiene los valores X, es decir, los valores de las variables aleatorias para las que se va a calcular la función de distribución o la función de densidad. Cuando se calcula una distribución discreta, los valores X deben ser enteros y positivos. Las estructuras de datos permitidas son Valor escalar, Serie de datos y Matriz de datos. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||||||||||||||||||
Distribution |
Especifica qué distribución debe calcularse y si debe calcularse la función de distribución o la función de densidad. El argumento Distribution puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||||||||
Parameter1 |
Especifica el primer parámetro de la distribución que se va a calcular. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||||||||||||||||
Parameter2 |
Especifica el segundo parámetro de la distribución que se va a calcular, si es necesario. Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
Notas
El resultado es siempre el tipo de datos En coma flotante de 64 bits.
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución normal con valor esperado μ y varianza σ² vienen dadas por:
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución logarítmica normal con los parámetros μ y σ² vienen dadas por:
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución exponencial con el parámetro α (parámetro de escala inverso) vienen dadas por:
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución Weibull con los parámetros α y β (parámetros de forma) vienen dadas por:
Nota: En la bibliografía, la vida útil característica T se utiliza a menudo como alternativa al parámetro α (y β se etiqueta como k). En este caso se aplica la siguiente relación:
Asimismo, en la bibliografía se utiliza a menudo el parámetro de escala inversa λ = 1/T en lugar del parámetro α. Por lo tanto, se aplica lo siguiente:
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución Chi-cuadrado con el parámetro n (número de grados de libertad) vienen dadas por:
P(n1,n2) denota aquí la función gamma incompleta regularizada.
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución t de Student con el parámetro n (número de grados de libertad) vienen dadas por:
I(z,n1,n2) denota aquí (y en lo sucesivo) la función beta incompleta regularizada.
La densidad de probabilidad continua f(x) y la función de distribución F(x) de la distribución F (distribución de Fisher) con los parámetros m (número de grados de libertad en el denominador) y n (número de grados de libertad en el numerador) vienen dadas por:
La densidad de probabilidad discreta f(k) y la función de distribución F(x) de la distribución binomial con los parámetros n (número de ensayos) y p (probabilidad de éxito o acierto) vienen dadas por:
La densidad de probabilidad discreta f(k) y la función de distribución F(x) de la distribución de Poisson con el parámetro λ (tasa media de eventos) vienen dadas por:
Disponibilidad
Opción Estadística
Ejemplos
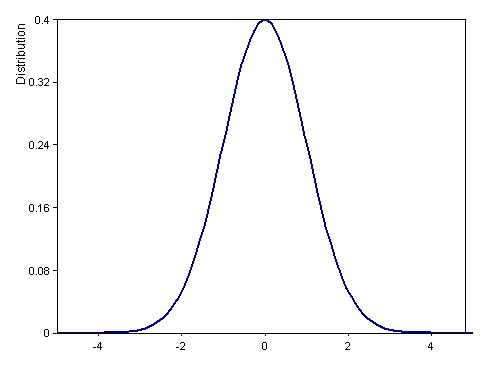
Dim x = Series(-5, 5, 0.05)
Signal(Distribution(x, DISTRIBUTION_NORMAL + DISTRIBUTION_DENSITY, 0, 1), x)
Calcula la función de densidad de la distribución normal típica (valor esperado 0, varianza 1) en el intervalo [-5, 5].
Véase también
Objeto de análisis Distribución
Bibliografía
[1] "Hartung, Joachim": "Statistik, 9. Auflage". "Oldenbourg Verlag GmbH, München", 1993. ISBN 3-486-22055-1.