Calcula la integral.
Sintaxis
Integral(Signal [ , Mode = INTEGRAL_TRAPEZOIDAL ])
o
Integral(Amplitude, Time [ , Mode = INTEGRAL_TRAPEZOIDAL ])
La sintaxis de la función Integral consta de los siguientes elementos:
Parte |
Descripción |
||||||||
|---|---|---|---|---|---|---|---|---|---|
Signal |
La señal cuya integral se va a calcular. Si el argumento es una serie de datos o una matriz de datos, se asume uno como incremento dX para la integración. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||||
Amplitude |
El componente Y de la señal que se va a integrar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||
Time |
El componente X de la señal que se va a integrar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||||
Mode |
Para el cálculo discreto de la integral se utilizan fórmulas de aproximación de distintos órdenes de precisión. El argumento Mode puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado INTEGRAL_TRAPEZOIDAL si no se especifica el argumento. |
Notas
El resultado es siempre el tipo de datos En coma flotante de 64 bits.
La unidad del resultado es igual al producto de las unidades de los componentes Y y X de Signal. Los valores se convierten en números en coma flotante de 64 bits antes del cálculo. Para matrices de datos y series de señales, el cálculo se realiza columna por columna. Los componentes X y Z, si existen, se transfieren sin cambios al resultado.El resultado puede considerarse la función maestra de la señal.
La integral se calcula en el modo INTEGRAL_TRAPEZOIDAL utilizando la fórmula trapezoidal (suponiendo al menos dos puntos de datos):
La regla trapezoidal también puede aplicarse a conjuntos de datos muestreados no equidistantes.
En el modo INTEGRAL_SIMPSON, la integral se calcula mediante la regla de Simpson. La regla de Simpson requiere conjuntos de datos muestreados de forma equidistante (suponiendo al menos tres puntos de datos):
En el modo INTEGRAL_CUBIC, la integral se calcula mediante una fórmula de integración cúbica. Esta fórmula de integración es la forma centralizada de la fórmula de integración de Adams (Adams interpolation formula o Ngo integrator, véase [4]). La norma también exige conjuntos de datos muestreados de forma equidistante (suponiendo al menos cuatro puntos de datos):
En todos los modos, la integral en el borde izquierdo I[0] se define como 0. Para la regla de Simpson y la fórmula de integración cúbica, no hay suficientes puntos de soporte en los márgenes I[1] y en el caso cúbico en el margen derecho I[N] para la fórmula de aproximación. En estos puntos, se utilizan reglas de cálculo que tienen el mismo orden de precisión (de forma análoga a [2, página 98]).
En general: Cuanto mayor sea el orden de precisión al seleccionar la fórmula de integración, mayor será la precisión al determinar la integral para conjuntos de datos suaves (no ruidosos). Sin embargo, si los conjuntos de datos son ruidosos, el error numérico en la determinación de la integral aumenta si se utiliza una fórmula de integración de orden superior. Por lo tanto, la elección del modo de integración debería depender del ruido/suavidad del conjunto de datos subyacente.
Sin embargo, si le interesa el espectro de frecuencias, es útil considerar las fórmulas de integración como filtros digitales (véase también [1] o [3, sección 7.2]). Las fórmulas de integración tienen la siguiente respuesta de amplitud. También se registra el integrador ideal (curva de filtro de la integración continua):
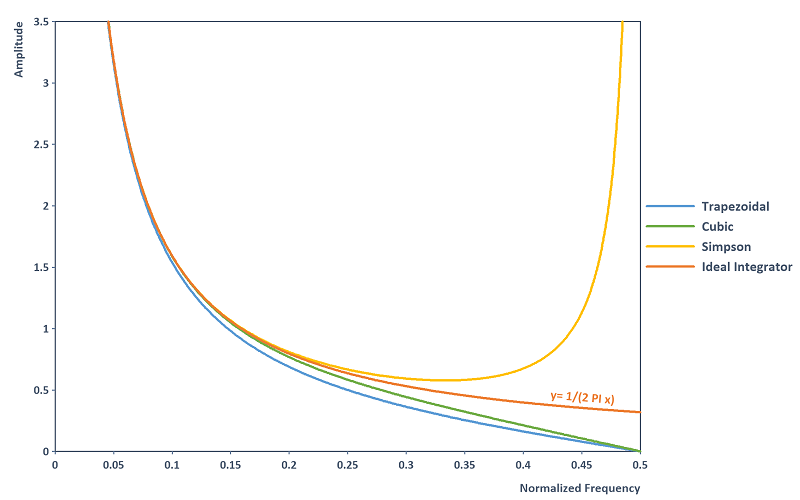
Observación: La regla trapezoidal y la fórmula de integración cúbica tienen una característica natural de paso bajo debido a la subestimación del integrador ideal y suprimen el ruido de alta frecuencia. La fórmula de integración cúbica tiene una aproximación más precisa de la respuesta de amplitud del integrador ideal en todo el dominio de la frecuencia que la regla trapezoidal. La regla de Simpson tiene la aproximación más exacta de la respuesta de amplitud del integrador ideal en el dominio de la frecuencia hasta aproximadamente 0,25, pero diverge en el rango del límite de Nyquist 0,5. Por tanto, la regla de Simpson amplifica el ruido de alta frecuencia. Cabe señalar que todas las reglas de aproximación tienen una respuesta de fase constante de -90 grados y, por lo tanto, corresponden a la respuesta de fase del integrador ideal.
Disponibilidad
FlexPro View, Basic, Professional, Developer Suite
Ejemplos
Integral({1,2,3,2,1}, {0,1,2,3,4})
Calcula la integral {0, 1.5, 4, 6.5, 8} de la serie de datos especificada como argumento utilizando la regla trapezoidal.
Integral(Signal)[-1]
Calcula el área bajo la curva de una señal. Para ello, hay que tomar el último valor del resultado.
Integral(Detrend(Signal))
Integra una señal periódica y elimina previamente el valor medio. En este caso se ha utilizado la función Detrend para eliminar el componente de CC o una tendencia lineal o adaptativa de la señal antes de la integración. Explicación: Si integra señales periódicas con un valor medio distinto de cero, la curva integrada se escapará por acumulación del valor medio en la señal. El siguiente gráfico ilustra la situación:
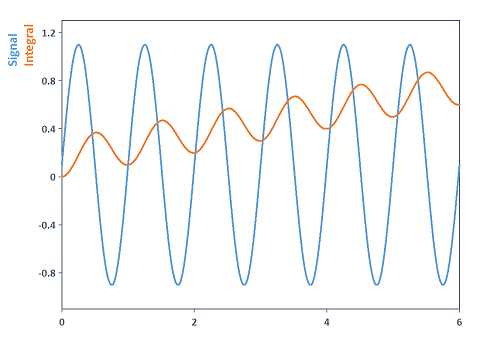
Integral(DCRemovalFilter(Signal))
Integra una señal y elimina previamente la desviación o el componente de CC. Para eliminar la desviación o el componente de CC, se utiliza la función DCRemovalFilter en lugar de la función Detrend. Explicación: La razón de la desviación de la señal tras la integración no es solo la acumulación del componente de CC durante la integración, sino también la respuesta de amplitud del integrador, que es inversamente proporcional a la frecuencia. Esto amplifica el ruido a frecuencias cercanas al componente de CC y lo eleva a valores arbitrariamente elevados mediante la integración. A continuación, la curva integrada se escapa. Para evitar la desviación, no basta con restar la media, sino que también hay que cortar los componentes de frecuencia cercanos al componente de CC mediante un filtro de paso alto. El siguiente gráfico ilustra la situación (como ejemplo, para la integración se ha utilizado una de las señales de aceleración de los datos de ejemplo de FlexPro ubicados en C:\Users\Public\Documents\Weisang\FlexPro):
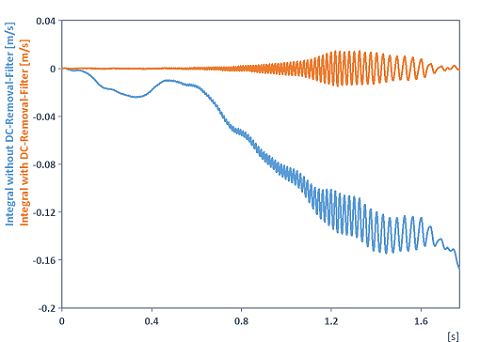
Dim filterCoef = List("b", {1/3, 4/3, 1/3}, "a", {1, 0, -1})
AmplitudeResponse(filterCoef)
Calcula la respuesta de amplitud del filtro de Simpson utilizando la función AmplitudeResponse.
Dim x = Series(0, 6, 0.5)
Integral(Signal(2.2 + 6.2*x + 12.6*x^2 - 2*x^3, x), INTEGRAL_CUBIC)
Calcula la integral de un polinomio de tercer grado en los puntos de soporte x. El resultado corresponde a la integral exacta Signal(2.2*x + 3.1*x^2 + 4.2*x^3 - 0.5*x^4, x).
Dim x = (30, 1, 0.1)
Dim f = Signal(50 * 1/x, x)
Dim integralExact = Signal(50 * log(x), x)
Absolute(Integral(f, INTEGRAL_TRAPEZOIDAL)[-1] - integralExact[-1])
Determina el error al calcular la integral numérica de la función suave f = 50 * 1/x para el modo INTEGRAL_TRAPEZOIDAL. El error es proporcional a 0,01. Sin embargo, si selecciona INTEGRAL_SIMPSON, se produce un error proporcional a 0,001. Si selecciona INTEGRAL_CUBIC, obtiene la máxima precisión con un error proporcional a 0,0001.
Véase también
Función SavitzkyGolayDerivative
Objeto de análisis Análisis de señales
Bibliografía
[1] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York, http://www.springer.com/de/book/9783319169842, 2015. ISBN 3-540-23165-X.
[2] C. Woodford, C. Phillips: Numerical Methods with Worked Examples. Chapman and Hall, 2-6 Boundary Row, London SE1 8HN, UK, 1997. ISBN 0-412-72150-3.
[3] Richard G. Lyons: Understanding Digital Signal Processing (3rd Edition). Prentice Hall, 2011. ISBN 0-13-702741-9.
[4] N. Q. Ngo: A new approach for the design of wideband digital integrator and differentiator. En: IEEE Trans. Circuits Syst. II, Exp. Briefs, Vol. 53, No. 9, Pages 936-940. Prentice Hall, 2006.