Calcula la primera derivada.
Sintaxis
Derivative(Signal [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])
o
Derivative(Amplitude, Time [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])
La sintaxis de la función Derivative consta de los siguientes elementos:
Parte |
Descripción |
||||||
|---|---|---|---|---|---|---|---|
Signal |
La señal cuya primera derivada se calcula. Si el argumento es una serie de datos o una matriz de datos, se asume uno como incremento dX para la derivada. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||
Amplitude |
El componente Y de la señal que se va a procesar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||
Time |
El componente X de la señal que se va a procesar. Si especifica una señal, se utiliza su componente Y. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal, Serie de señales y Serie de señales con componente X bidimensional. Se permiten todos los tipos de datos numéricos. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. |
||||||
Mode |
Para la aproximación discreta de la derivada se utilizan diferencias finitas en forma de cocientes de diferencias centrales. El orden de las diferencias finitas utilizadas determina la precisión del cálculo numérico de la derivada. El argumento Mode puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado DERIVATIVE_CENTRAL_3_POINTS si no se especifica el argumento. |
Notas
El resultado es siempre el tipo de datos En coma flotante de 64 bits.
La unidad del resultado es igual al cociente de las unidades de Amplitude y Time o de los componentes Y y X de Signal. Para matrices de datos y series de señales, el cálculo se realiza columna por columna. Los valores se convierten en números en coma flotante de 64 bits antes del cálculo. Los componentes X y Z, si existen, se transfieren sin cambios al resultado.La derivada numérica se calcula en el modo DERIVATIVE_CENTRAL_3_POINTS para conjuntos de datos muestreados equidistantemente (incremento dX) utilizando el siguiente cociente de diferencias centrales (suponiendo al menos tres puntos de datos):
Este caso corresponde a una promediación de los cocientes de diferencias unilaterales derecha e izquierda, es decir:
La derivada numérica se calcula en el modo DERIVATIVE_CENTRAL_5_POINTS para conjuntos de datos muestreados equidistantemente utilizando el siguiente cociente de diferencias centrales (suponiendo al menos cinco puntos de datos):
Para ambas variantes, no hay suficientes puntos de soporte disponibles en los márgenes para calcular las diferencias centrales. Por lo tanto, la derivada numérica se calcula utilizando cocientes de diferencias finitas no centrales del mismo orden. Las reglas de cálculo en los márgenes se especifican en [1].
Las reglas de cálculo especificadas para la derivación numérica también pueden generalizarse para conjuntos de datos muestreados de forma no equidistante, véase [1]. Estas reglas de cálculo también se implementan en FlexPro y se utilizan automáticamente en cuanto el conjunto de datos subyacente tiene un muestreo no equidistante.
En general: cuanto mayor sea el orden al seleccionar las diferencias finitas, mayor será la precisión al determinar la derivada para conjuntos de datos suaves (no ruidosos). Sin embargo, si los conjuntos de datos son ruidosos, el error numérico en la determinación de la derivada aumenta cuando se utiliza un orden superior al seleccionar las diferencias finitas. Por lo tanto, la elección del modo de derivación también debería depender del ruido o la suavidad del conjunto de datos subyacente. El modo DERIVATIVE_CENTRAL_5_POINTS está prescrito para evaluaciones de choque, por ejemplo, véanse las directrices J1727 de [2] y ECE-R94 de [3].
Sin embargo, si le interesa el espectro de frecuencias, es útil considerar las reglas de derivación como filtros digitales (véase también [4]). Las reglas de derivación tienen la siguiente respuesta de amplitud. También se registran el diferenciador ideal (curva de filtro de la diferenciación continua) y la diferenciación hacia delante y hacia atrás utilizando la función Diff:
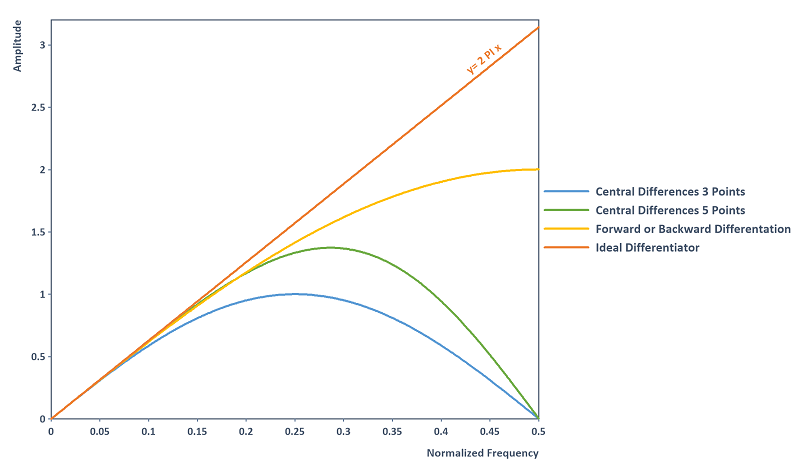
Observación: la regla central de 3 puntos y la regla central de 5 puntos suprimen el ruido de alta frecuencia en el rango del límite de Nyquist 0,5. La regla central de 5 puntos tiene una aproximación de respuesta de amplitud del diferenciador ideal más precisa en todo el dominio de la frecuencia que la regla central de 3 puntos. Aunque los cocientes diferenciales unilaterales hacia delante y hacia atrás también tienen una aproximación de respuesta de amplitud del diferenciador ideal más precisa, amplifican el ruido de alta frecuencia. Cabe señalar que las reglas de las diferencias centrales tienen una respuesta de fase constante de 90 grados y, por tanto, corresponden exactamente a la respuesta de fase del diferenciador ideal. En cambio, los cocientes de diferencias hacia delante y hacia atrás tienen un desplazamiento de fase lineal.
Disponibilidad
FlexPro View, Basic, Professional, Developer Suite
Ejemplos
Derivative(Signal)
Calcula la derivada discreta de cualquier señal utilizando la regla central de 3 puntos.
Derivative({1.0, 3.0, 5.0, 5.0, 4.0, 3.0})
Calcula la derivada {2, 2, 1, -0.5, -1, -1} de la serie de datos especificada como argumento, asumiendo 1.0 como incremento dX. El resultado tiene la misma longitud de conjunto de datos que el conjunto de datos de entrada.
Diff({1.0, 3.0, 5.0, 5.0, 4.0, 3.0}, DIFF_QUOTIENT_FORWARD)
Calcula los cocientes de diferencias de valores vecinos utilizando la función Diff y devuelve {2, 2, 0, -1, -1} como resultado. La función Diff utiliza diferencias finitas no centrales (de primer orden). La longitud del conjunto de datos del resultado se reduce en uno con respecto al conjunto de datos de entrada.
Dim x = Series(-6, 6, 0.5)
Derivative(Signal(2.2 + 6.1*x + 3.6*x^2 + 12*x^3 - x^4, x), DERIVATIVE_CENTRAL_5_POINTS)
Calcula la derivada de un polinomio de cuarto grado en los puntos de soporte x. El resultado coincide con la derivada exacta Signal(6.1 + 7.2*x + 36*x^2 - 4*x^3, x).
Dim x = Series(-3, 3, 0.1)
Dim f = Signal(Sin(x^2), x)
Dim derivExact = Signal(2*x*Cos(x^2), x)[[ 1.0 ]]
Absolute(Derivative(f, DERIVATIVE_CENTRAL_3_POINTS)[[ 1.0 ]] - derivExact)
Determina el error para el modo DERIVATIVE_CENTRAL_3_POINTS calculando la derivada numérica de la función suave f = Sin(x2) en el punto 1.0. El error es proporcional a 0,01. Si, por el contrario, se selecciona DERIVATIVE_CENTRAL_5_POINTS, esto proporciona una mayor precisión con un error proporcional a 0,0001. Si utiliza la función Diff en su lugar, la derivada se calcula con un error proporcional a 0,1 (precisión mínima). En general, para aproximar la derivada debe darse preferencia a la función Derivative frente a la función Diff.
Véase también
Función SavitzkyGolayDerivative
Objeto de análisis Análisis de señales
Bibliografía
[1] Bengt Fornberg: Generation of Finite Difference Formulas on Arbitrarily Spaced Grids. En: Mathematics of Computation, Vol. 51, No. 184, Pages 699-706. https://doi.org/10.1090/S0025-5718-1988-0935077-0, 1988.
[2] Safety Test Instrumentation Stds Comm: Calculation Guidelines for Impact Testing (J1727). En: SAE International. http://standards.sae.org/j1727_201502/, 2015.
[3] UN Vehicle Regulations: Regulation No. 94 - Frontal collision protection (ECE-R94). En: Concerning the Adoption of Uniform Technical Prescriptions for Wheeled Vehicles, Equipment and Parts which can be Fitted and/or be Used on Wheeled Vehicles and the Conditions for Reciprocal Recognition of Approvals Granted on the Basis of these Prescriptions. http://www.unece.org/trans/main/wp29/wp29regs81-100.html, 2013.
[4] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York, http://www.springer.com/de/book/9783319169842, 2015. ISBN 3-540-23165-X.